基于改进局部递归率的脉动风速非平稳度分析方法

李利孝， 肖仪清， 郑 斌， 宋丽莉

（1．哈尔滨工业大学深圳研究生院，广东深圳518055；2．中国气象局公共气象服务中心，北京100081）

基于改进局部递归率的脉动风速非平稳度分析方法

李利孝1， 肖仪清1， 郑 斌1， 宋丽莉2

（1．哈尔滨工业大学深圳研究生院，广东深圳518055；2．中国气象局公共气象服务中心，北京100081）

为了克服递归趋势（recurrence trend，RT）指标对不同信号非平稳度估计存在误判的缺陷，分别采用互信息法和伪临近法确定了递归量化分析的最佳延迟时间和最小嵌入维数，然后在递归量化分析基础上，提出了归一化局部递归率标准差（standard deviation of normalized local recurrence rate，SDNLRR）作为信号非平稳度量化指标．利用该指标，通过递归量化分析方法分析了白噪声信号、正弦信号、调幅信号、线性调频信号4个基本信号和2个实测台风场脉动风速信号的非平稳特性，并与传统的递归趋势指标分析结果进行了对比．研究结果表明：利用SDNLRR指标对6个信号的非平稳度的量化比较准确率达100%，比RT指标的准确率提高了33．33%，消除了RT指标对正弦信号和平稳脉动风速信号的错误估计．

非平稳度；递归量化分析；局部递归率；脉动风速

天气系统是一种复杂的非线性动力系统，它的发展演化同时受到大气层结构状况、近地面摩擦作用以及湍流驱动机制等多种相互作用且连续变化因素的影响，从而导致实测湍流风速信号具有一定程度的非平稳特征和非高斯特性．现代信号处理的主要分析手段（如谱分析等）以及基于随机振动理论的结构动力响应计算方法均建立在平稳随机过程假设基础上，对于平坦开阔场地，常态风作用下结构动力抗风设计基本满足该假定．然而对于复杂地形条件，或者处于台风、雷暴等极端天气过程条件下的动力抗风设计，则很难满足平稳性假设［1］．

脉动风速非平稳度的强弱决定了其分析方法的选取以及结构风振响应计算结果的精度和可靠性．通常所用的非平稳检验方法（例如轮次检验、逆序检验）从时间序列的均值与方差等低阶统计量出发［2］，仅能给出定性的判别结果，不能对脉动风速的非平稳度进行量化分析．

本文从递归分析出发，通过定义新的递归量化分析指标——归一化局部递归率标准差法（standard deviation of normalized local recurrence rate，SDNLRR）对时间序列的非平稳度进行刻画．通过对高斯白噪声信号、正弦信号、调幅信号、线性调频信号以及两个实测脉动风速信号进行非平稳度对比分析来验证SDNLRR指标的有效性．

1 递归图

递归现象在自然界中十分普遍，例如潮汐涨落、日夜更替等．在动力系统理论中，递归现象是指系统中的某一特定状态在不同时刻具有相似的特性．尽管递归现象很早就被人们所认识，但是直到1987年Eckmann等提出递归图［3］概念之后，人们才真正掌握了对其进行定性分析和定量描述的手段．递归分析通常包括3部分：（1）相空间重构；（2）递归图绘制；（3）递归量化分析．

1．1 相空间重构

根据Takens的相空间重构理论［4］，系统中的任一分量的演化和发展过程均是该系统中其他分量对其进行作用和影响的结果，因此，系统中与某一分量有关的信息都将在该分量的时间序列中得到体现．通过时间延迟可将单变量时间序列i＝1，2，…，N｝嵌入到由嵌入维数m和延迟时间τ重构的m维相空间中，即：

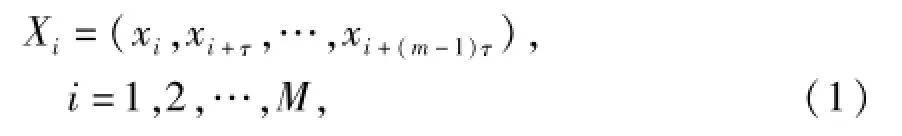
式中：M为m维重构相空间的向量数，

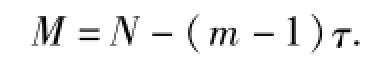
为了保证重构的相空间能够重现原系统的特性，必须合理选择嵌入维数m与延迟时间τ．Takens证明了当嵌入维数m≥2d＋1（d为吸引子关联维数）时，重构相空间与原系统在拓扑意义上等价，该关系式提供了无限长无噪声序列下嵌入维数的选取准则，在该种情况下延迟时间可以任意选取．然而，通常时间序列为有限长度且伴有噪声，因此嵌入维数m和延迟时间τ的选取在相空间重构的过程中十分重要．

对于m和τ的选取主要分为两种观点：第一种认为，嵌入维数m和延迟时间τ之间并无直接联系，可以分别求取，例如，用G-P算法、伪临近法、改进伪临近法及求取最佳延时的自相关函数法和互信息法等求取嵌入维数m；另一种观点认为两者之间存在相关关系，其中比较具有代表性的是C-C算法．

本文分别选取了应用较广的互信息法（mutual information function，MIF）［5］和伪临近法（false nearest neighbours，FNN）［6］确定最佳延迟时间τ和最小嵌入维数m．

在给定系统A情况下可得到系统B信息量的大小，称为系统A与B之间的互信息，通过计算原始时间序列之间的互信息，可求得在不同延时τ时两者之间的关联程度．由于延迟时间τ选取的基本原则是使序列中两点之间的相互影响最弱，可以通过改变延迟时间τ，选取其首次得到最小τ值时作为最优延迟时间．

伪临近点是指两个在m维重构相空间中接近的点在m＋1维空间发生了远离，否则称作真临近点．当嵌入维数小于系统真实维数时容易产生伪临近点，当嵌入维数m达到或超过系统真实维数时伪临近点将消失．因此，通过计算不同嵌入维数时伪临近点所占比例，找出该比例降至比较稳定的低水平时所对应的嵌入维数即为最小嵌入维数．

图1为分别用互信息法以及伪临近法在某脉动风速时程相空间重构过程中确定延迟时间以及嵌入维数的示意图，从图1中可以得到嵌入维数m＝5，延迟时间τ＝5．

1．2 递归图

用文献［3］的方法构造递归矩阵R，与延迟后的序列

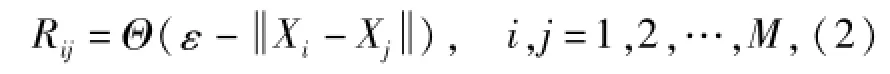
式中：Rij为递归矩阵的元素；

Θ（·）为单位阶跃函数；

ε为预先给定的邻域半径．

图1 相空间重构参数Fig．1 Parameters for the phase space reconstruction

递归图是递归矩阵的一种可视化表达形式，从式（2）可见，矩阵R是一个由0和1组成的M×M阶方阵．计算点在整个区域填充，当Rij＝1时，在递归图上用黑点表示，意味着从状态Xi出发，经过一段时间后，在状态Xj发生了递归；当Rij＝0时，在递归图上用白色表示，意味着两种状态远离．由于任意状态均与其本身递归，因此递归图的主对角线（line of identity，LOI）为一黑实线．邻域半径ε的选取依据目前尚无定论，若过小会增大噪声影响，而过大则会引起虚假递归．本文以保证递归率在1%左右的方法来选取的邻域半径ε值［7］．

2 递归量化分析

递归图的主要分析方法包括定性递归分析及量化递归分析［8］．前者利用总结归纳得到的递归图模式对一些简单信号的特征作出判别；后者使用量化分析手段，更适用于湍流等复杂信号．递归量化分析方法［8］是由Webber和Zbilut提出的，根据递归点在递归图上的分布特征，递归量化指标主要包括递归率γRR、确定性DET、测度熵ENT、递归趋势RT、层状度LAM和平均捕获时间TT等．在这些量化指标中，与非平稳特征相关的主要是递归率RR和递归趋势RT．

递归率RR用来度量递归点密度的大小，可以反映相点在m维空间中的聚集程度以及递归频率的大小，其定义为

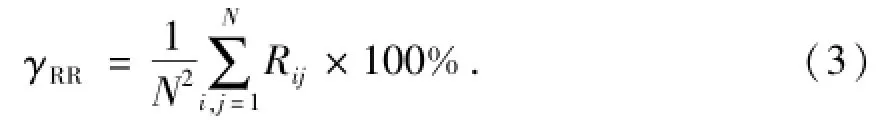
递归趋势RT用来表征递归率随着延时的变化趋势，其定义为

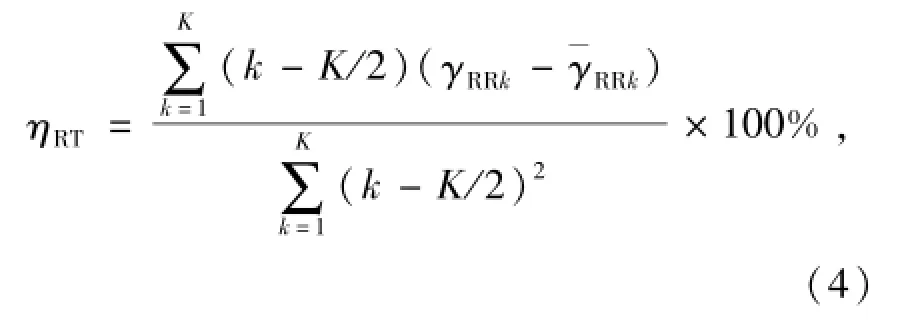
式中：K为将递归图副对角线下方的三角形区域按平行副对角线方向等距分割成的区块数，其取值通常应当满足N－K＞10；

γRRk为区块k（k＝1，2，…，K）内的递归率，称之为局部递归率．

递归趋势表征局部递归率γRRk关于k的线性回归斜率值．对于一个完全平稳的时间序列，其局部递归率应是一个常数，不随时间间隔发生变化，递归趋势为0；而对于一些时变的非平稳系统，其局部递归率将随着时间间隔发生变化．目前这种方法得到了广泛的应用［9-11］．

然而，由于递归趋势是通过最小二乘法线性回归的斜率值，因此，比较适用于具有漂移模式特征的信号，而对于一些局部非平稳性较强但总体趋势稳定的信号，可能会出现误判．湍流信号成分复杂，除了漂移模式外可能还同时存在突变模式等，使用递归趋势来衡量湍流信号可能会存在问题．为了克服递归趋势RT的这一局限性，在这里定义归一化局部递归率标准差SDNLRR来衡量信号的非平稳程度，其定义为

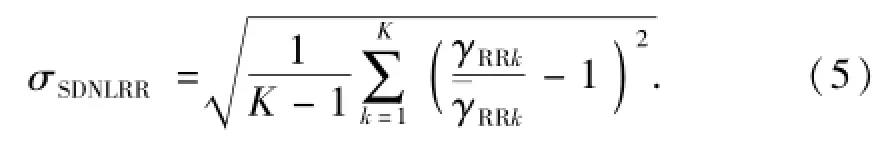
归一化局部递归率标准差σSDNLRR的实质是局部递归率的变异系数．非平稳度越强，σSDNLRR值越大，完全平稳时σSDNLRR值为0．与ηRT相比，σSDNLRR对于递归率的局部突变更加敏感，对一些模式复杂的非平稳信号分析更有效．另外，由于ηRT是递归率的线性拟合斜率，而递归率的大小又受到邻域半径ε的影响，因此，同一信号的邻域半径ε不同时，其计算得到的递归趋势也不同，这对同一个时间序列来说极不合理．而σSDNLRR通过局部递归率均值对不同区块的局部递归率归一化，在一定程度上削弱了邻域半径选取对非平稳程度刻画的影响．

食物有保质期，信息资源也会有。过了期的信息资源就如同昨日黄花一文不值。作为工程造价而言，是为工程做铺垫的一项工作，对于时间肯定有着严格的要求。因为工程造价对于工程而言是一个必要且充分的条件，但又不能因为它的拖延而推迟工程的期限[4]。所以，为了造价方案在预计时间段内做出对于信息资源就必须以最快的速度获取，并且是最新的、具有时效性的信息资源。而大数据下的计算机和各类系统恰如其分地解决了这个问题。

3 数值模拟及实测验证

3．1 信号来源

为了验证本文定义的非平稳度量化指标σSDNLRR的有效性，选取信号S1～S6进行验证．

（1）理论上平稳的高斯白噪声信号S1由MATLAB的randn函数生成．

（2）正弦信号S2为x（t）＝sin（2π×0．02t）．

（3）线性调频信号S3为x（t）＝sin（2πf1t），ft＝5×10－5t＋0．02，可以产生线性变化的频率为0．02～0．08 Hz正弦调频信号．

（4）调幅信号S4为x（t）＝A［1＋M× cos（2πfmt）］sin（2πfct），式中：载波幅值A＝1；载波基频fc＝0．02 Hz；调制频率fm＝0．005 Hz；调制幅度为50%．

（5）同时通过逆序检验与轮次检验的“平稳”脉动风速时程信号S5选自台风黑格比过程的实测脉动风速时程．

（6）未通过逆序检验和轮次检验的非平稳脉动风速时程S6选自了台风黑格比过程的实测脉动风速时程．

在验证的过程中，同时计算了传统的ηRT值作为对比，信号S1～S6的时程曲线如图2所示，各信号采样频率均为1 Hz，样本长度N均为600．

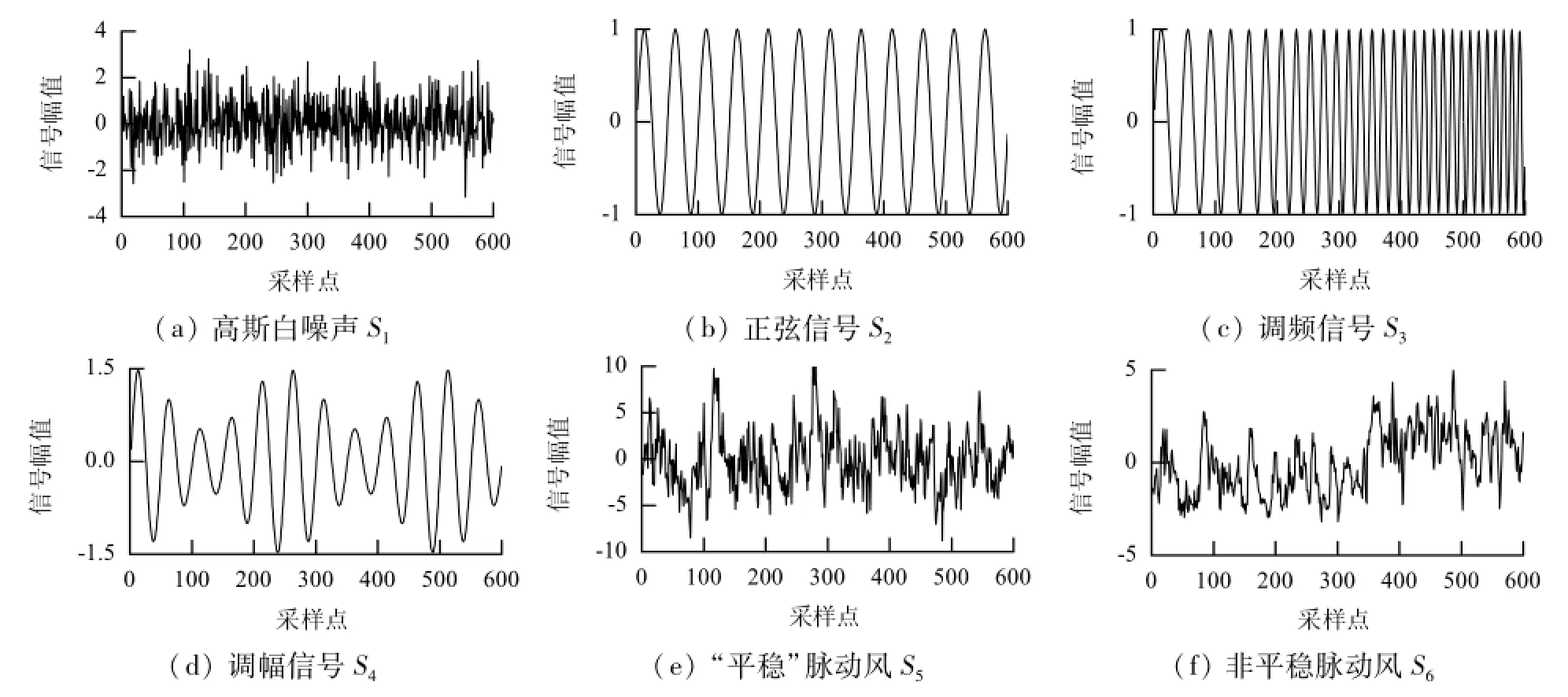
图2 信号时程图Fig．2 Time history of the signals

3．2 递归图及递归分析

采用第1节所述方法对上述6个信号进行相空间重构和递归图绘制．为了统一标准，K值均取为10，按照控制总体递归率为1%左右的准则选取邻域半径ε，嵌入维数m和延迟时间τ分别采用伪临近法（FNN）和互信息法（MIF）计算．根据上述参数，计算了信号S1～S6的递归图及相应的局部递归率，见图3和图4．利用上述递归图及相应的局部递归率结果，根据式（4）和（5）分别计算了各信号的ηRT和σSDNLRR，见表1．

从图3、4及表1可见，高斯白噪声信号S1的递归点整体分布均匀，其ηRT值及σSDNLRR值均为所测试的6种信号中最小，因此，两种方法都能较好地表征白噪声信号的非平稳度．

正弦信号S2是一种平稳性较好的周期信号，虽然其递归图不如信号S1分布均匀，但整体分布规则，表现出许多与主对角线平行的直线．从S2的局部递归率分布图可见，除第10区块由于面积过小引起误差偏大外，其余区块的局部递归率波动较小．但正是由于γRR10的影响使得S2的ηRT＝－0．081 2，高于调幅信号S4，很不合理；其σSDNLRR值则为0．196 0，略大于信号S1，小于调频信号S3与调幅信号S4，与实际情况相符．

调频信号S3的递归图呈现了漂移模式，其局部递归率具有单调变化的趋势，因此存在着比较明显的非平稳性．从图3可见，递归点在主对角线附近集中，γRR1约为2．2，明显大于平均值；信号S3的

两者均反映出信号的非平稳特性，相对而言，σSDNLRR更显著．

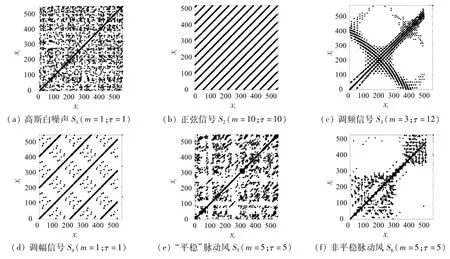
图3 信号递归图Fig．3 Recurrence plots of the signals

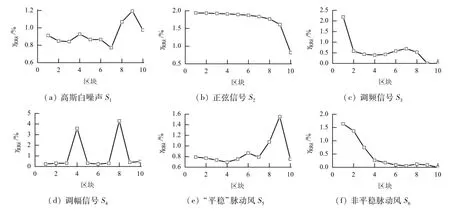
图4 信号局部递归率Fig．4 Local recurrence rate of the signals

理论上调幅信号S4较正弦信号S2的平稳性更差，其递归图的也证明了这一点．S4的递归图仅由几条与主对角线平行的直线构成，整体均匀程度较S2差，非平稳性比S2更显著．从S4的局部递归率图上可以看到，除γRR4和γRR8外，其他区块递归率为0．然而，由于S4的局部递归率变化比较对称，其ηRT值仅为0．068 3，小于信号S2，未能反映出该信号应有的非平稳特征；相对而言，σSDNLRR＝2．121 7则更加合理．

分别计算信号S5和S6的指标ηRT与σSDNLRR，从图3（e）和图3（f）可见，信号S5的递归点分布较S6更均匀，因此，S5比S6的平稳性更好，符合实际情况．S5的ηRT＝0．040 6，σSDNLRR＝0．282 7，与平稳信号S1和S2接近，表明信号S5较为平稳．信号S6递归图上的递归点集中于左下角和右上角，分布不均匀．对照信号S6的时程可以发现，在约350 s风速发生了突变，因此S6的非平稳性明显，其ηRT＝－0．168 2，σSDNLRR＝1．428 3．因此，采用指标σSDNLRR对脉动风速时程进行非平稳程度量化描述是合理有效的．

综上所述可见，传统的递归趋势TND对上述6个信号中的正弦信号和调幅信号的非平稳度进行量化分析时存在估计不准确的问题，而采用本文定义的归一化局部递归率标准差SDNLRR可以准确地对上述6个信号的非平稳度进行量化分析，适用于实测脉动风速信号的非平稳特性分析．

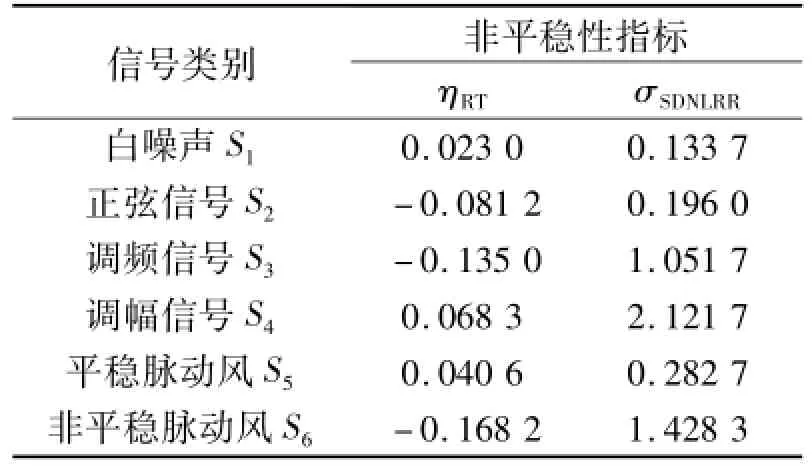
表1 平稳度量化指标比较Tab．1 Comparison between quantitative non-stability indicatorsηTNDandσSDNLRR

4 结束语

脉动风速的非平稳性度量及其合理设计是结构抗风设计中亟待解决的问题，本文基于递归量化分析方法，对传统的非平稳性度量指标进行了改进，提出了归一化局部递归率标准差σSDNLRR对时间序列的非平稳性进行表征，并使用了4种通用信号和两个实测脉动风速信号进行了比较验证．结果表明，与传统的非平稳性指标（递归趋势指标ηRT等）相比，本文提出的归一化局部递归率标准差σSDNLRR对信号非平稳性的表征更合理．

本文方法通过对局部递归率进行归一化，在一定程度上削弱了由不同样本之间总体递归率的差别引起的非平稳性差异．通过计算局部递归率的标准差而不是对其斜率进行线性拟合，扩展了非平稳性指标的适用范围．最后，对实测“平稳”脉动风速和非平稳脉动风速的验证结果表明，指标σSDNLRR能较好地表征不同实测脉动风速的非平稳性．

［1］ CHEN J，XU Y L．On modelling of typhoon-induced non-stationary wind speed for tall buildings［J］．The Structural Design of Tall and Special Buildings，2004，13（2）：145-163．

［2］ BECK T W，HOUSH T J，WEIR J P，et al．An examination of the runs test，reverse arrangements test，and modified reverse arrangements test for assessing surface EMG signal stationarity［J］．Journal of Neuroscience Methods，2006，156（1）：242-248．

［3］ ECKMANN J，KAMPHORST S O，RUELLE D．Recurrence plots of dynamical systems［J］．Europhysics Letters，1987，4（9）：973-977．

［4］ TAKENS F．Detecting strange attractors in turbulence［M］．［S．l．］：Springer，1981：366-381．

［5］ FRASER A M，SWINNEY H L．Independent coordinates for strange attractors from mutual information［J］．Physical Review A，1986，33（2）：1134-1140．

［6］ KENNEL M B，BROWN R，ABARBANEL H D．Determining embedding dimension for phase-space reconstruction using a geometrical construction［J］．Physical Review A，1992，45（6）：3403-3411．

［7］ ZBILUT JP，ZALDIVAR-COMENGES J，STROZZIF．Recurrence quantification based Liapunov exponents for monitoring divergence in experimental data［J］．Physics Letters A，2002，297（3）：173-181．

［8］ WEBBER C L，ZBILUT JP．Dynamical assessment of physiological systems and states using recurrence plot strategies［J］．Journal of Applied Physiology，1994，76（2）：965-973．

［9］ ZBILUT J P，THOMASSON N，WEBBER C L．Recurrence quantification analysis as a tool for nonlinear exploration of nonstationary cardiac signals［J］．Medical Engineering and Physics，2002，24（1）：53-60．

［10］ 闫润强．语音信号动力学特性递归分析［D］．上海：上海交通大学，2006．

［11］ 杨栋，任伟新，李丹，等．基于局部递归率分析的振动信号非平稳评价［J］．中南大学学报：自然科学版，2013，44（7）：3024-3032．YANG Dong，REN Weixin，LI Dan，et al．Local recurrence rate analysis based non-stationarity measurement for operational vibration signal［J］．Journal of Central South University：Science and Technology，2013，44（7）：3024-3032．

（中文编辑：秦萍玲 英文编辑：兰俊思）

Method for Analysis of Non-stationarity of Fluctuating Winds Based on Revised Local Recurrence Rate

LI Lixiao1， XIAO Yiqing1， ZHENG Bin1， SONG Lili2
（1．Shenzhen Graduate School，Harbin Institute of Technology，Shenzhen 518055，China；2．Public Meteorological Service Center，China Meteorological Administrator，Beijing 100081，China）

In order to overcome the misestimate of the non-stationarity of different signals by the recurrence trend（RT），the mutual information function and false nearest neighbors are employed to determine the time delay and minimum embedding dimension of the recurrence quantification analysis（RQA），respectively．Then a novel index，i．e．，the standard deviation of normalized local recurrence rate（SDNLRR），which is based on the RQA，was proposed to quantify the non-stationary degree of the signals．Utilizing the SDNLRR，the non-stationarity of four basic signals（white noise signal，sinusoidal signal，amplitude-modulated signal and linear frequency modulation signal）and two field observed fluctuating wind speed histories were analyzed and compared with the analysis results of RT．The results show that the proposed SDNLRR could offer a quantitative comparison of the nonstationarity of the above six signals with a 100%accuracy．The new method eliminates the misestimates of the sinusoidal signal and the stationary fluctuating wind speed signal in RT，and hence is more accurate than the RT estimation by 33．33%．

non-stationarity；recurrence quantification analysis；local recurrence rate；fluctuating winds

TU973．213

A

0258-2724（2016）01-0065-06

10．3969／j．issn．0258-2724．2016．01．010

2014-07-30

国家自然科学基金资助项目（51308168，51278161）；中国博士后科学基金资助项目（2013M531045，2014T70343）

李利孝（1984—），男，博士，研究方向为结构风工程，电话：18682013431，E-mail：lilixiao1984＠gmail．com

李利孝，肖仪清，郑斌，等．基于改进局部递归率的脉动风速非平稳度分析方法［J］．西南交通大学学报，2016，51（1）：65-70．