相空间中含时滞的非保守力学系统的Noether定理*
金世欣,张 毅
(1.苏州科技学院 数理学院,江苏 苏州 215009;2.苏州科技学院 土木工程学院,江苏 苏州 215009)
时滞现象普遍存在于自然界和工程实际中,从自然界到人类社会,从自然科学、工程技术到社会科学,时间滞后现象无处不在[1]。即使一个很简单的问题,一旦考虑时滞的影响,就使得动力学行为变得更为复杂,也更为接近力学本质[1-3]。而力学系统的对称性对其动力学行为及其基本性质都具有深刻的影响,从基本理论到具体应用都显示出对称性的极端重要性[4-16]。考虑含时滞的变分问题的研究可追溯到El’sgol’c[17]的工作;1968年,Hughes[18]讨论了含时滞的变分和最优控制问题,建立了含时滞的Euler-Lagrange方程;随后,Palm和Schmitendorf[19],Rosenblueth[20],Chan和Yung[21]以及Lee和Yung[22]对含时滞的变分问题做了进一步的研究。然而,含时滞的变分对称性与守恒量的研究才刚刚开始。2012年,Frederico和Torres[23]首次讨论了含时滞的变分和最优控制问题的Noether对称性,得到了含时滞的Euler-Lagrange方程以及含时滞的最优控制问题的Hamilton正则方程,并讨论了含时滞的Lagrange系统和最优控制Hamilton系统在点变换下的Noether对称性与守恒量。2013年,张毅和金世欣[24-25]研究了含时滞的非保守系统动力学的Noether理论,建立了含时滞的非保守系统的Lagrange方程,给出了含时滞的Noether对称变换、准对称变换以及广义准对称变换的定义和判据,建立了在速度依赖的无限小群变换下含时滞的非保守力学系统的Noether理论,并将其进一步推广到含时滞的Hamilton系统的Noether对称性与守恒量。
本文进一步研究相空间中含时滞的非保守力学系统的Noether对称性与守恒量。给出相空间中含时滞的非保守系统的Hamilton原理,建立含时滞的非保守系统的Hamilton正则方程;在依赖于广义速度的无限小群变换下,给出含时滞的Hamilton作用量的变分公式,建立相空间中含时滞的非保守力学系统的Noether广义准对称变换的定义和判据;研究含时滞的Noether广义准对称性与守恒量之间的联系,得到相空间中含时滞的非保守力学系统的Noether定理。
1 含时滞的非保守系统的Hamilton正则方程
设力学系统的位形由n个广义坐标qs(s=1,2,…,n)来确定,考虑系统具有时滞,其Lagrange函数为[24]
(1)
引进含时滞的广义动量和Hamilton函数
(s=1,2,…,n)
(2)
H=H(t,ps,qs,psτ,qsτ)=
(3)
含时滞的非保守系统的Hamilton原理为
(4)
qs(t)=δs(t),t1-τ≤t≤t1
(5)
qs(t)=qs(t2),t=t2,(s=1,2,…,n)
(6)
其中时滞常量τ (7) 进行变量替换t=θ+τ,并考虑条件(5),有 (8) 将(8)式代入(7)式,得到 (9) 利用分部积分计算,并考虑边界条件(5)和(6),得 (10) 以及 (11) 将式(10)和(11)代入式(9),得到 (12) 将式(3)两边对广义动量求偏导数,得到 t1≤t≤t2-τ, (13) ps(t)+psτ(t+τ)- t1≤t≤t2-τ, t2-τ (14) 将式(14)对时间t求导,有 (15) 相空间中含时滞的Hamilton作用量为 (16) 引入r-参数有限群的无限小变换 ps(t)+Δps(t) (s=1,2,…,n) (17) 其展开式为 (18) (19) 式(19)也可写为 (20) 其中 (σ=1,2,…,r) (21) 式(19)和(20)是相空间中含时滞的Hamilton作用量的变分的两个基本公式。 下面我们来建立相空间中含时滞的Noether广义准对称变换的定义和判据。 假设H′是某个另外的Hamilton函数,若变换(17)精确到一阶小量满足 (22) 则称这种不变性为相空间中含时滞的Hamilton作用量在无限小变换(17)下的广义准不变性,而变换(17)称为相空间中含时滞的Noether广义准对称变换。于是有 定义1 若含时滞的Hamilton作用量(16)在无限小群变换(17)作用下,满足条件 (23) 其中ΔG=εσGσ,Gσ=Gσ(t,ps,qs,psτ,qsτ)为规范函数,则称无限小变换(17)为相空间中含时滞的Noether广义准对称变换。 由定义1和变分公式(19),(20)式,得到如下判据。 判据1 如果无限小群变换(17),当t1≤t≤t2-τ时,满足条件 (24) 当t2-τ (25) 则变换(17)是相空间中含时滞的Noether广义准对称变换。 式(24)和(25)也可写成:当t1≤t≤t2-τ时,有 (26) 当t2-τ (27) 当r=1时,式(26)和(27)称为相空间中含时滞的非保守力学系统的Noether等式。 判据2 如果无限小群变换(18),当t1≤t≤t2-τ时,满足条件 (σ=1,2,…,r) (28) 当t2-τ (29) 则变换(18)是相空间中含时滞的Noether广义准对称变换。 利用判据1或判据2,可以判断相空间中含时滞的非保守力学系统的Noether对称性。 对于相空间中含时滞的非保守力学系统(13)和(15),若能够找到系统的Noether广义准对称变换,便可求得相应的守恒量。有如下定理: 定理1 对于相空间中含时滞的非保守力学系统,如果无限小群变换(17)是相空间中含时滞的Noether广义准对称变换,则系统存在r个线性独立的守恒量,当t1≤t≤t2-τ时,形如 (30) 当t2-τ (31) 证明将相空间中含时滞的非保守力学系统的运动微分方程(13)和(15)代入式(28)和(29),由定义1和判据2,得到:当t1≤t≤t2-τ时 (32) 当t2-τ (σ=1,2,…,r) (33) 对式(32)和(33)积分,便得到结果。证毕。 定理1称为相空间中含时滞的非保守力学系统的Noether定理。由定理1知,如果能找到系统的一个Noether广义准对称变换,便可能得到系统的一个守恒量。 例已知含时滞的力学系统的Lagrange函数为 (34) 非势广义力为 (35) 由(2)式,得到 (36) 则系统的运动微分方程为 t∈[t1,t2-τ]; (37) 由Noether等式(26)和(27),得到 (38) (39) 方程(38)有解 (40) 方程(39)有解 t∈(t2-τ,t2] (41) 生成元(40)和(41)相应于所论含时滞的非保守系统的Noether对称性,根据定理1,系统有如下守恒量 t∈[t1,t2-τ] (42) t∈(t2-τ,t2] (43) 式(42)和(43)是所论相空间中含时滞的非保守系统相应于Noether对称性(40)和(41)的Noether守恒量。 文中研究了相空间中含时滞非保守力学系统的Noether对称性与守恒量。建立了含时滞的非保守力学系统的运动微分方程;依据相空间中含时滞的Hamilton作用量的两个基本公式,定义了相空间中含时滞的Noether广义准称变换,给出了相空间中含时滞的Noether广义准称变换的判据;建立了相空间中含时滞的非保守力学系统的Noether对称性与守恒量之间的联系。本文的结果具有普遍性,可以进一步拓展到含时滞的最优控制系统、含时滞的Birkhoff系统等。 [1] 徐鉴, 斐利军. 时滞系统动力学近期研究进展与展望[J]. 力学进展, 2006, 36(1): 17-29. [2] 胡海岩, 王在华. 非线性时滞动力学系统的研究进展[J]. 力学进展, 1999, 29(4): 501-512. [3] 王在华, 胡海岩. 时滞动力系统的稳定性与分岔:从理论走向应用[J]. 力学进展, 2013, 43(1): 3-20. [5] LUTZKY M. Dynamical symmetries and conserved quantities[J]. J Phys A: Math Gen, 1979, 12(7): 973-981. [6] HOJMAN S A. A new conservation law constructed without using either Lagrangians or Hamiltonians[J].J Phys A: Math Gen, 1992, 25: L291-L295. [7] 赵跃宇. 非保守力学系统的Lie对称性和守恒量[J]. 力学学报, 1994, 26(3): 380-384. [8] 梅凤翔. 李群和李代数对约束力学系统的应用[M]. 北京: 科学出版社, 1999. [9] 梅凤翔. 约束力学系统的对称性与守恒量[M]. 北京: 北京理工大学出版社, 2004. [10] 王树勇, 梅凤翔. 相空间中完整约束系统的形式不变性[J]. 中山大学学报:自然科学版, 2002, 41(6): 10-13. [11] FU J L, CHEN L Q, CHEN B Y. Noether-type theory for discrete mechanico-electrical dynamical systems with nonregular lattices[J]. Sci China: Phys Mech Astron, 2010, 53(9): 1687-1698. [12] 张毅. 非完整力学系统的Hamilton对称性[J]. 中国科学: 物理学 力学 天文学, 2010, 40(9): 1130-1137. [13] 张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报:自然科学版, 2013, 52(4): 45-50. [14] 龙梓轩,张毅. 基于按正弦周期律拓展的分数阶积分的变分问题的Noether定理[J]. 中山大学学报:自然科学版, 2013, 52(5): 51-56. [15] LUO S K, LI L. Fractional generalized Hamiltonian equations and its integral invariants[J]. Nonlinear Dynamics, 2013, 73(1/2): 339-346. [16] ZHANG Y, ZHOU Y. Symmetries and conserved quantities for fractional action-like Pfaffian variational problems[J]. Nonlinear Dynamics, 2013, 73(1/2): 783-793. [17] EL’SGOL’C L E. Qualitative methods in mathematical analysis[M]. Providence: American Mathematical Society, 1964. [18] HUGHES D K. Variational and optimal control problems with delayed argument[J]. J Optim Theory Appl, 1968, 2(1): 1-14. [19] PALM W J, Schmitendorf W E. Conjugate-point conditions for variational problems with delay argument[J].J Optim Theory Appl, 1974, 14(6): 599-612. [20] ROSENBLUETH J F. Systems with time delay in the calculus of variations: a variational approach[J]. IMA J Math Control Inform, 1988, 5(2): 125-145. [21] CHAN W L, YUNG S P. Sufficient conditions for variational problems with delayed argument[J]. J Optim Theory Appl, 1993, 76(1): 131-144. [22] LEE C H, Yung S P. Sufficient conditions for optimal control problems with time delay[J]. J Optim Theory Appl, 1996, 88(1): 157-176. [23] FREDERICO G S F, TORRES D F M. Noether’s symmetry theorem for variational and optimal control problems with time delay[J]. Numerical Algebra, Control and Optimization, 2012, 2(3): 619-630. [24] 张毅, 金世欣. 含时滞的非保守系统动力学的Noether理论[J]. 物理学报, 2013, 62(21): 214502. [25] JIN S X, ZHANG Y. Noether symmetry and conserved quantity for a Hamilton system with time delay[J]. Chinese Physics B, 2014, 23(5): 054501.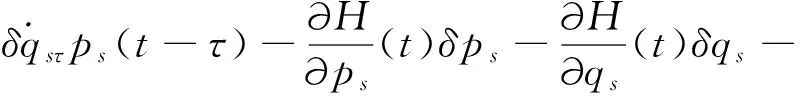




2 相空间中含时滞的Hamilton作用量的变分





3 相空间中含时滞的Noether广义准对称变换

4 相空间中含时滞的非保守力学系统的Noether定理
5 算 例
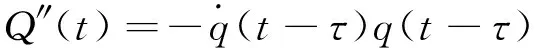



6 结 论

