一类线性二次正倒向随机最优控制问题

唐 雷

（山东科技大学，山东 青岛 266590）

0 引言

本文研究了下面的正倒向随机控制系统

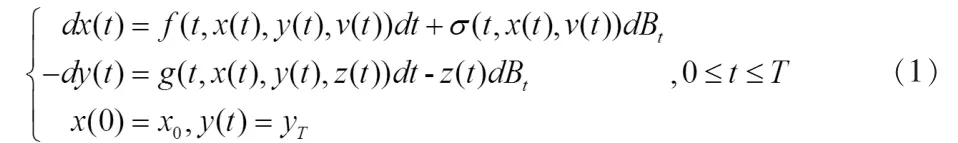
设(Ω,F,P)为一概率空间，其中x0是给定的，yT是Ft可测的随机变量，{Bt}t≥0为 d 维标准布朗运动，信息流 Ft＝σ{Bs,0≤s≤t}，v(t)∈U⊂Rk我们定义如下允许控制集Uad：，定义指标泛函

并且

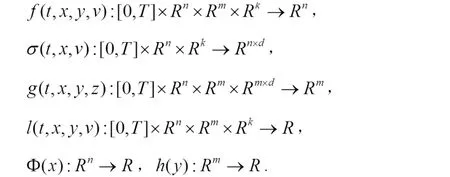
若有 ，则称 u(·)为最优控制，(x(·),y(·),z(·),u(·))为控制系统（1）的最优解。

当控制域U是Rk中的一个非空凸子集时，我们做如下假设：

i）f,σ,g,l,Φ,h关于各自的自变量是连续可微的；

ii）f,σ,g关于各自自变量的导数有界；

iii）lx,ly,lv都被界住，Φx被 c(1+x )界住，hy被界住。其中c为正常数。

吴臻[1]将控制系统（1）推广，并在控制域为凸集的情况下得到完全耦合的正倒向随机控制系统的最大值原理，由此我们可以根据[1]得到如下结论：

定理 1 （随机最大值原理）若(x(·),y(·),z(·)；u(·))是正倒向随机控制系统（1）的最优解，则有

其中哈密顿函数H如下：

H(t,x,y,z,v,p,q,k)＝〈p,-g(t,x,y,z)〉+〈q,f(t,x,y,v)〉+〈k,σ(t,x,v)〉+l(t,x,y,v)，其中(p(·),q(·),k(·))是下面对偶方程的解：

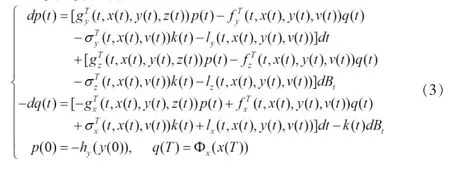
本文基于王向荣等[2]中控制系统研究了一类线性二次正倒向随机控制系统的最优控制问题，在下面的一节，根据肖华、吴臻[3]的思想方法，运用定理1得到线性控制系统的控制解的显示形式。第三节，验证所得到的显示表达式为最优控制，并证明唯一性。

1 控制的显示表达式

本节来研究下面的线性正倒向随机控制系统：

指标泛函如下：

显然，（4）、（5）分别为（1）、（2）的特殊情形。为了简化记号，我们将这里的Bt规定为一维布朗运动，A(w),C(w)为n×n阶矩阵，B(w),D(w)为n×k阶矩阵，vt,t≥0是一个取值于U⊂Rk的允许控制过程，并且Ft可测、平方可积。R(w),Q(w),L(w)是n×n阶非负定对称矩阵，N(w)是一个k×k阶正定对称矩阵，并存在逆为N-1。由定理1可得相应于线性正倒向随机控制系统（4）的对偶方程为：

当(x(·),y(·),z(·),u(·))为最优解时，由吴臻[2]可知对偶方程（6）存在唯一解(p(·),q(·),k(·))，与之相应的哈密顿函数 H 为：

H(t,x,y,z,v,p,q,k)＝

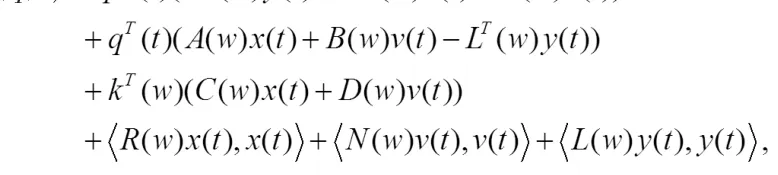
进而有 Hv(t,x,y,z,u,p,q,k)＝BT(w)q(t)+DT(w)k(t)+2N(w)u(t)。

容易验证（4）、（5）满足假设条件（i）、（ii）、（iii），由定理 1 可得：

〈Hv(t,x,y,z,v,p,q,k),v-u(t)〉≥0，

即〈BT(w)q(t)+DT(w)k(t)+2N(w)u(t),v-u(t)〉≥0，∀v∈Uad,a.e.,a.s.，进一步可得到：

定理 2 若(x(·),y(·),z(·),u(·))是系统（4）和（5）的最优解，那么系统控制的显示表达式为：

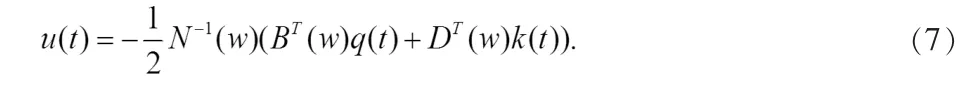
2 最优控制的唯一性

本节我们证明定理2中所得到的控制u(t)为线性二次正倒向随机最优控制系统（4）和（5）的唯一最优控制。

定理3 定理2中的u(t)是正倒向随机控制系统（4）和（5）的唯一最优控制。

证明：先验证u(·)为最优控制。设控制u(·)相应的轨线为(x(t),y(t),z(t))，对于任意的允许控制 v(·)∈Uad，其轨线为(xv(·),yv(·),zv(·))，则

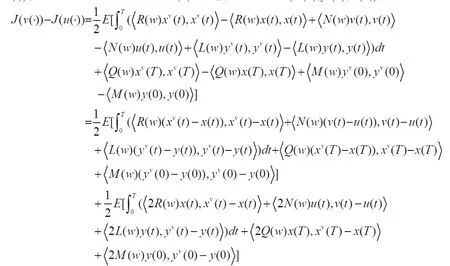
因为 p(0)＝-2M(w)y(0),q(T)＝2Q(w)x(T)，所以

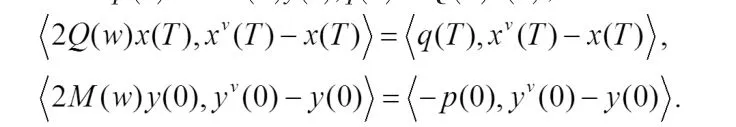
对〈q(t),xv(t)-x(t)〉和〈p(t),yv(t)-y(t)〉分别运用 公式并积分取期望得：

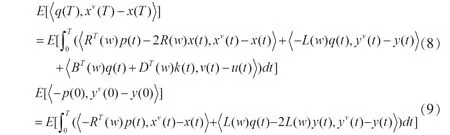
因为 R(w),L(w),Q(w),M(w)都为非负定对称矩阵，将上面（8）、（9）两式带入 J(v(·))-J(u(·))中得到 J(v(·))-J(u(·))≥0。 所以得到 u(t)＝-12N-1(w)(BT(w)q(t)+DT(w)k(t))是线性二次正倒向随机最优控制问题（5）的最优控制。

下面我们再证明最优控制的唯一性，仍沿用经典的平行四边形法则方法[4-5]。

设 u1(·),u2(·)都是最优控制，且 u1(·)≠u2(·)，与之相应的轨线分别为(x1(t),y1(t),z1(t)),(x2(t),y2(t),z2(t))。由最优控制定义，我们可得

从而可得u1(t)＝u2(t),a.e.,a.s.，唯一性得证。

［1］Wu Zhen.Maximum Principle for Optimal Control Problem of Fully Coupled Forward-Backward Stochastic Systems[J].System Science and Mathematical Science,1998,11(3).

［2］Wang,X.R，Gao,Z.Y，Wu,Z.：Forward-Backward Stochastic Differential Equation and the Liner Quadratic Stochastic Optimal Control[J].ACTA AUTOMATICA SINICA，2003,29(1)：32-37.

［3］肖华,吴臻.一类线性二次正倒向随机最优控制系统的最优控制问题[C]//程代展,王行愚.第二十三届中国控制会议论文集.上海：华东理工大学出版社,2004：99-103.

［4］Pontryagin L S.Boltyanskii B T.Gamkrelidze R V，Mishchenko E F.The Mathematical Theory of Optimal Processes[M].New York：Interscience，1962.

［5］Bensoussan A.Lectures in stochastic control.In：Proceedings Cortona，Lecture Notes in Mathematics[M].New York：Springer,1981,972(1)：1-62.