基于探地雷达的高铁无砟轨道结构层病害检测
廖红建, 朱庆女, 昝月稳, 谢勇勇, 孙俊煜
(1.西安交通大学人居环境与建筑工程学院,陕西西安710049;2.西南交通大学地球科学与环境工程学院,四川成都610031)
基于探地雷达的高铁无砟轨道结构层病害检测
廖红建1, 朱庆女1, 昝月稳2, 谢勇勇1, 孙俊煜1
(1.西安交通大学人居环境与建筑工程学院,陕西西安710049;2.西南交通大学地球科学与环境工程学院,四川成都610031)
为了检测高速铁路(高铁)无砟轨道混凝土结构内部在施工过程中产生的缺陷,避免在高速列车荷载作用下发展成路基病害,运用探地雷达技术对高铁无砟轨道结构进行了二维正演模拟分析.基于有限差分法,在时间域上推导了探地雷达二维正演模拟方程.针对易形成高铁无砟轨道病害缺陷的多种复杂工况,建立了CRTSⅡ型板式无砟轨道的地电模型,分别对CA砂浆层不同填充程度、CA砂浆层硬化过程进行了二维正演数值模拟,分析了探地雷达二维正演模拟图像的特征.模拟结果表明,二维正演模拟可以清楚地分辨板式无砟轨道结构内不同介质层的分界面,以及钢筋的数目和位置.
交通工程;高速铁路;无砟轨道;路基病害;探地雷达;正演数值模拟
无砟轨道具有坚固耐用、变形小、变形累积缓慢、整体性强及稳定性好等优点,已在国内外高速铁路得到广泛应用[1-2].高速铁路(高铁)无砟轨道通常是整体封闭的混凝土结构,由于钢筋密布,使得混凝土内的不密实、裂缝易被忽视[1].
无砟轨道施工过程中造成的缺陷、隐患,会使高铁无砟轨道结构在高速列车荷载反复冲击震动下发育成为铁路病害.设计过程中钢筋粗细、间距设置不当,也会使无砟轨道产生裂缝、破损,从而引发病害[2].因此,对高铁无砟轨道在设计、施工过程中以及后期运营阶段进行病害缺陷检测,发现隐患并及时防治,具有重要意义[3-5].
目前,运用探地雷达技术对高铁无砟轨道路基病害缺陷进行检测处于发展阶段.探地雷达是通过用高频率的电磁波传播性质来检测地下结构内部物质分布规律的地球物理勘探方法,属无损检测.该技术可以对高铁轨道进行全面、高效、无损排查,所得结果以剖面图像显示.但是,探地雷达电磁波在地下结构中传播时,由于复杂目标物的反射、散射、介质分布的非均匀性以及地质构造的复杂性、多样性等,使得识别实际记录的雷达剖面图像比较困难,加之人工解译图像过程中存在的不确定因素,最终影响检测结果判别[6-8].因此,需要结合实地检测情况对各种典型路基病害的探地雷达进行正演模拟分析,以识别复杂的探地雷达图像,建立路基病害图像数据库,为探地雷达的自动化检测和反演提供基础.
正演数值模拟作为探地雷达检测结果的解译以及反演的基础理论依据,可以探明雷达波在地下结构中的传播规律,提高探地雷达检测结果的解释精度.
我国用于高速铁路的无砟轨道形式有CRTSⅠ和CRTSⅡ型板式无砟轨道、CRTSⅠ和CRTSⅡ型双块式无砟轨道4种,本文中主要根据高速铁路CRTSⅡ型板式无砟轨道结构特征和结构层内的病害缺陷,基于时域有限差分法建立探地雷达正演数值计算模型,分析无砟轨道中砂浆层缺陷和路基沉降病害的探地雷达图像特征,以期为高铁线路施工及运营期的雷达检测应用提供理论分析基础.
1 时域有限差分法
1.1 探地雷达的二维正演模拟方程[9]
时域有限差分法是在时间域上计算电磁场的数值方法[10].在无源区域同性介质中,Maxwell旋度方程的微分形式为
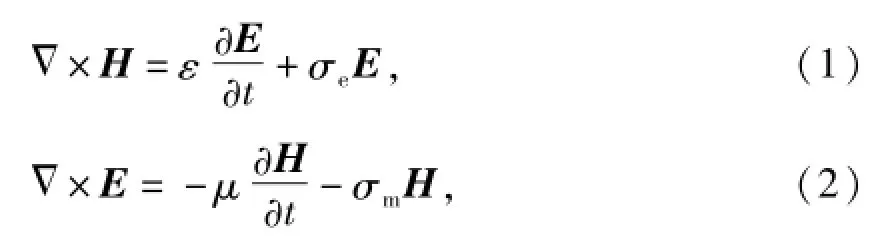
式中:E为电场强度;H为磁场强度;ε为介质介电常数;μ为磁导系数;σe为电导率;σm为磁导率.
电磁波在地下介质传播过程中,主要以横磁波(TM)形式传播.对二维空间TM波,所有物理量均与z坐标无关.采用YEE氏网格进行二阶精度的中心差分,近似将直角坐标下的Maxwell旋度方程转化为差分形式[11].导出二维空间TM波时域的有限差分方程,即探地雷达的二维正演模拟方程:

式中:参数m的取值与左端场分量节点的空间位置相同;Hx、Hy和Ez分别为电、磁场在TM波下的分量;Δt为时间步长.
从式(3)~(5)可见,电磁场在时间顺序上交替抽样,抽样时间间隔相差半个时间步.由给定的相应电磁问题的初始值,利用时域有限差分法即可求得各时刻空间电磁场的分布[12-13].
本文主要基于时域有限差分原理,用商用软件GprMax进行探地雷达正演模拟计算.
1.2 数值稳定性问题
由于Maxwell旋度方程转化为差分方程时,采用的是显示差分格式,这种差分格式存在稳定性问题.因此,为了使方程的数值解最终收敛、稳定,用时域有限差分法计算时,需要合理地选取时间步长和空间步长.
对于二维TM波,x、y坐标方向网格的空间步长Δx=Δy=Δs.因此,TM波的数值稳定性条件为

式中,vmax为电磁波传播速度.
由式(6)可见,进行时域有限差分计算时,需首先选择网格步长,然后才能确定时间步长.时域有限差分法是通过将连续的介质离散为网格节点进行计算的,而离散后必然会导致电磁波的数值发生频散.因此,为了降低频散效果,需对网格大小进行一定限制,网格大小应满足

式中,λmin为电磁波在介质中传播时的最小波长.
1.3 数值色散问题
由于时域有限差分方程中是用近似差商来替代原Maxwell旋度方程中的连续微商,因此,模拟电磁波传播时,在非色散媒质空间中也会出现色散现象,称为数值色散.
1.4 吸收边界条件
由于计算机容量的限制,时域有限差分法的计算只能在有限区域进行,导致网格空间截断处出现非物理的电磁波反射现象.而边界吸收条件能保证边界场计算的必要精度,消除非物理因素引起的入射到截断边界的波的反射.采用GprMax软件中设置的完全匹配层(perfectly matched layer,PML).
2 板式无砟轨道结构的正演数值模拟及试验验证
2.1 正演数值模拟
正演数值模拟分析主要针对高铁CRTSⅡ型板式无砟轨道.
高铁CRTSⅡ型板式无砟轨道[14]主要由配套扣件、钢轨、预制道床板、CA砂浆调整层和混凝土支撑层组成,见图1.其中,预制道床板为标准轨道板,每块标准轨道板均有10对承轨台,尺寸为6 450 mm×2 250 mm×200 mm,质量约8.63 t,混凝土设计强度为C55.
沿铁路延伸方向截取其中1对承轨台进行分析,纵向剖面配筋见图2,预应力钢筋为Φ10.

图1 CRTSⅡ型板式无砟轨道Fig.1 A cross-section of CRTSⅡslab ballastless track

图2 CRTSⅡ型板式无砟轨道沿线剖面结构配筋示意Fig.2 Reinforcement of CRTS Ⅱ slab ballastless track in a cross-section
根据CRTSⅡ型板式无砟轨道结构,建立探地雷达数值计算地电模型,见图3.模型尺寸为1.2 m× 1.0 m,断面介质层分为5层.第1层为空气层,厚0.3 m;第2层为混凝土轨道板,厚0.2 m,现场实测相对介电常数为8.6,电导率为0.001;第3层为砂浆垫层,厚0.03 m,现场实测相对介电常数为3.8,电导率为0.001;第4层为混凝土支撑层,厚0.17 m,介质材料与混凝土相近,电性参数同混凝土层;最下为路基土层,相对介电常数取12.上、下层钢筋网深度分别距离轨道板表面0.082和0.138 m,钢筋间距见图3(a=0.15 m,b=0.10 m;c=6.2 cm,d=5.6 cm,e=8.2 cm).
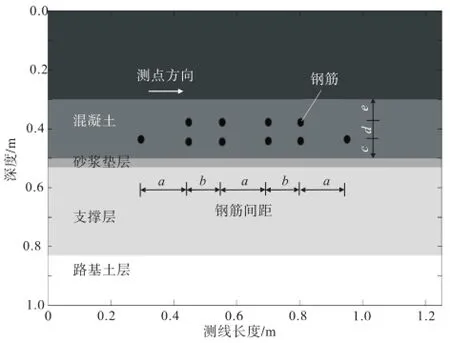
图3 CRTSⅡ型板式无砟轨道结构地电模型Fig.3 Geoelectric model for CRTS Ⅱ slab ballastless track
天线中心频率为2.6 GHz,步长为0.005 m.模拟网格步长应满足式(7),取网格步长Δx=Δy=Δs=0.001 m;时窗tw=15 ns,共220道扫描线,每条扫描线有6 360个扫描点;吸收边界条件选取完美匹配层,设20个网格层;激励源采用雷克子波.
根据时域有限差分正演数值模拟得到所计算空间的电磁场分量,导入并用Matlab读取、绘制成波形,生成CRTSⅡ型板式无砟轨道板的探地雷达剖面图(图4).结果表明,正演计算模型可以很好地模拟板式无砟轨道结构内部的情形,模拟图像特征清晰,位置准确,各层介质结构的反射界面明显:在传播时间4.0~4.5 ns处为砂浆垫层上下面反射信号,约10 ns处为混凝土支撑层与路基土层之间的分界面.
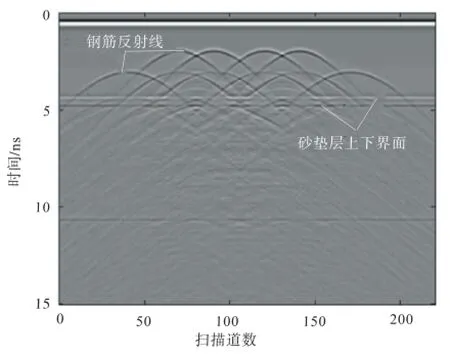
图4 CRTSⅡ型板式无砟轨道结构正演模拟Fig.4 Forward simulation of CRTS Ⅱ slab ballastless track
根据介质层反射深度h与雷达波传播速度v和传播时间t之间的关系式(8),可计算得砂浆垫层上下界面的反射深度范围为200~230 mm,混凝土支撑层与路基土层之间分界面的反射深度约500 mm,与实际板式无砟轨道结构吻合.

从图4还可以看出,探地雷达正演数值模拟图像中,可清楚地识别出钢筋的位置和数目.第1层介质中1、2层倒“V”形曲线分别为轨道板中上、下层钢筋的雷达反射信号特征曲线,每一条倒“V”形曲线代表1根钢筋.约1.5 ns处为第1层钢筋反射信号,共有4根钢筋,根据式(8)可计算出该层钢筋距轨道板表面70 mm;约2.5 ns处为第2层钢筋的反射信号,共有6根钢筋,同样可计算出该层钢筋距轨道板表面约130 mm,与实际的板式无砟轨道结构吻合.
2.2 试验验证
采用GSSI公司的SIR3000系列探地雷达,选取天线中心频率为2.6 GHz,对板式无砟轨道板进行检测,探地雷达图像经RoadDoctor软件处理后的图像见图5.
根据图像可以清晰地看到轨道板内的钢筋反射信号呈倒“V”形曲线,第1层双曲线顶点对应的时间为1.5 ns,根数为4根;第2层双曲线顶点对应的时间为2.5 ns,根数为6根,与实际结构中钢筋的位置和数目吻合.图5右侧为从雷达灰度剖面图中提取的其中的1道扫描线,从该扫描线的信号振幅可以清楚地看到雷达波的传播过程.在1.5和2.5 ns处,分别有2根钢筋使雷达反射信号振幅强烈;4.0~4.5 ns处又有强反射信号,与实际结构中CA砂浆层的表面深度吻合.与正演数值模拟结果——图4吻合,验证了探地雷达二维正演数值模拟高铁板式无砟轨道结构的可行性.

图5 砂浆层检测结果Fig.5 Test result of mortar layer
3 板式无砟轨道结构层病害的正演模拟
3.1 CA砂浆层不同填充程度的正演数值模拟
根据高铁CRTSⅡ型板式无砟轨道结构,CA砂浆层在灌浆施工过程中易灌浆不均匀,形成空洞病害等质量问题[15],因此,检测CA砂浆层是否存在缺陷对保证高铁的运行质量极其重要.
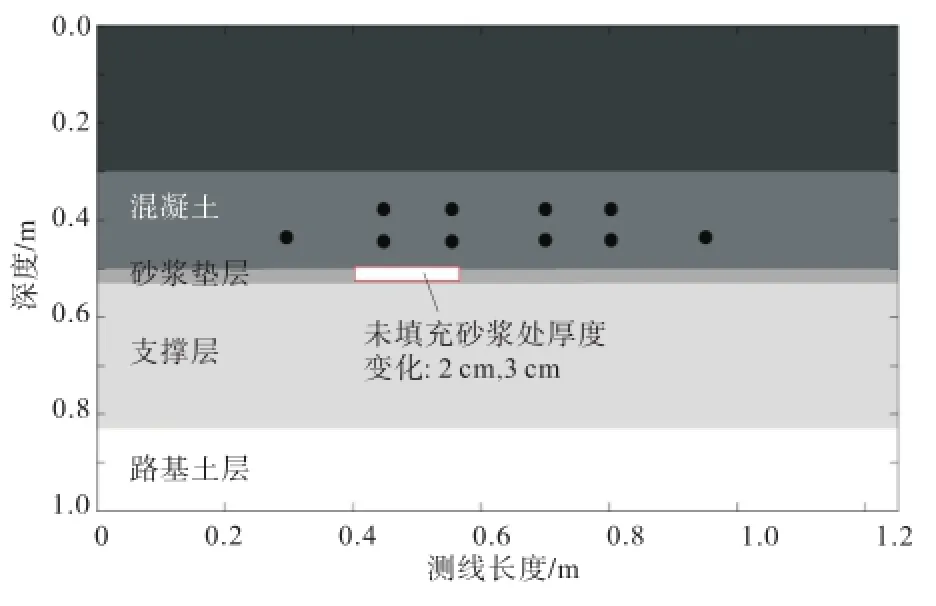
图6 未填充砂浆地电模型Fig.6 Geoelectric model for unfilled mortar
假设砂浆层中未填充砂浆部分宽10 cm,厚度分别为2和3 cm,内为空气介质,建立不同填充程度的CA砂浆层正演模拟地电模型,见图6.图7为砂浆层中未填充部分厚分别2和3 cm时的正演数值模拟结果.可见,不同填充程度砂浆层病害的探地雷达反射信号均有明显显示,能被探地雷达清晰地检测到.未填充砂浆层部分的界面反射信号强烈,界面反射明显,界面所在位置(即砂浆未填充处)和宽度范围可以从图中根据扫描步距和雷达波传播时间,依次定量判辨出来.而且,在不同填充程度的雷达图像中,反射界面的深度信息发生变化,实际检测中可以根据检测条件计算出CA砂浆层中脱空层的深度.

图7 不同未填充厚度砂浆层的正演模拟Fig.7 Forward simulation of mortar layer with different unfilled thicknesses
3.2 不同施工阶段CA砂浆层的正演数值模拟
高铁施工的CA砂浆层是通过灌浆完成的,从灌浆到硬化过程,CA砂浆层从流体状态转变成有承载力的硬化状态,其介电常数也会随之减小.因此,施工过程中,可以根据不同时间段砂浆状态改变时的介电常数值,用探地雷达技术对CA砂浆层的灌浆施工质量进行分析.
首先进行CA砂浆灌浆硬化过程的数值建模,通过改变砂浆层的介电常数模拟砂浆的动态硬化过程.假设施工过程中,CA砂浆层中有一宽10 cm、厚2 cm的空洞,其介电常数分别为81、25和12,从而建立3种不同介电常数的CA砂浆层地电模型,对应于液体流动态、硬化期固液共存状态和未完全硬化的固态CA砂浆层.计算得到的雷达正演模拟图像见图8.

图8 不同施工阶段砂浆层病害正演模拟图像Fig.8 Forward simulation diagrams of mortar layer disease at different construction stages
可见,CA砂浆灌浆以及硬化过程的探地雷达二维正演模拟图像,不仅可以很好地识别砂浆填充状态,还能识别不同阶段砂浆层界面的位置.砂浆层施工时,CA砂浆处于液体状态,流动性大,相对介电常数相应也大,砂垫层与上、下介质层介电特性差异明显,界面反射系数大,因此雷达波传播时,分界面的反射信号强烈,图像特征明显.由于不同阶段砂浆的状态不同,雷达电磁波速度发生变化,在砂浆层中的传播时间也相应不同.施工初期,经历时间最久,硬化过程中逐渐缩短,但砂浆层病害部分的雷达反射界面在砂浆层中的位置基本未发生变化.
4 结 论
本文根据高铁CRTSⅡ型板式无砟轨道结构特点,对砂浆层缺陷和路基沉降病害进行探地雷达正演数值模拟,分析了探地雷达图像特征,得到以下主要结论:
(1)建立无砟轨道CA砂浆层病害探地雷达地电模型,通过正演模拟分析了CA砂浆层中存在缺陷的探地雷达正演数值模拟图像.结果表明,所得图像与实际板式无砟轨道结构相符,各层介质结构和钢筋的反射界面明显.
(2)对施工过程中CA砂浆层硬化过程进行探地雷达正演模拟,得到了砂浆硬化过程中不同介电常数对应的探地雷达正演模拟图像特征.结果表明,探地雷达二维正演模拟图像能够很好地识别砂浆填充状态以及不同阶段砂浆层界面的位置.
[1] ESVELD C.Modern railway track[M].Zaltbommel:MRT-Production,2001:28-35.
[2] NAKAGAWA D,MASATOSHI H.Reevaluation of Japanese high-speed rail construction:recent situation of the north corridor Shinkansen and its way to completion[J].Transportation Policy,2007,14(2):150-164.
[3] 魏祥龙,张智慧.高速铁路无砟轨道主要病害(缺陷)分析与无损检测[J].铁道标准设计,2011(3):38-40.WEI Xianglong,ZHANG Zhihui.Major diseases(defects)analysis and nondestructive testing of highspeed railway[J].Railway Standard Design,2011(3):38-40.
[4] 刘振民,钱振地,张雷.双块式无砟轨道道床板混凝土裂缝分析与防治[J].铁道建筑,2007(6):99-101.LIU Zhenming,QIAN Zhendi,ZHANG Lei.Concrete crack analysis and prevention of double block ballastless track[J].Railway Engineering,2007(6):99-101.
[5] ADAM D,BRABDL H,PAULMICHL I.Dynamic aspects of rail tracks for high-speed railways[J].International Journal of Pavement Engineering,2010,11(4):281-291.
[6] NIGEL J,EDDIESR,DODSS.Void detection beneath reinforced concrete sections:the practical application of ground-penetrating radar and ultrasonic techniques[J].Journal of Applied Geophysics,2011,61(6):1636-1648.
[7] 李大心.探地雷达方法与应用[M].北京:地质出版社,1994:3-4.
[8] 陈理庆.雷达检测技术在结构无损检测中的应用研究[D].长沙:湖南大学土木工程学院,2008.
[9] 谢勇勇,廖红建,昝月稳.探地雷达检测铁路路基病害的二维正演模拟[J].浙江大学学报:工学版,2010,44(10):1907-1911.XIE Yongyong,LIAO Hongjian,ZAN Yuewen.Two dimensional forward simulation of railway roadbed disease based on ground penetrating radar technique[J].Journal of Zhejiang University:Engineering Science,2010,44(10):1907-1911.
[10] 葛德彪,闰玉波.电磁波时域有限差分方法[M].2版.西安:西安电子科技大学出版社,2005:8-9.
[11] YEE K S.Numerical solution of initial boundary value problems involving Maxwell's equation in isotropic media[J].IEEE Transactions on Antennas Propagations,1966,14(3):302-307.
[12] MUR G.Absorbing boundary conditions for the finitedifference approximation of the time-domain electromagnetic field equations[J].IEEE Transactions on Electromagnetic Compatibility,1981,23(4):377-382.
[13] TAFLOVE A.Review of the formulation and applications of the FDTD method for numerical modeling of electromagnetic wave interactions with arbitrary structures[J].Wave Motion,1988,10(6):547-582.
[14] 朱庆女,廖红建,谢勇勇,等.探地雷达正演模拟数据偏移后处理分析[C]∥龚晓南,谢永利,杨晓华,等.地基处理理论与实践新进展.北京:人民交通出版社,2014:173-179.
[15] 徐建,陈志华,王凯,等.板式无砟轨道垫层CA砂浆研究进展[J].华东交通大学学报,2009,26(4):58-62.XU Jian,CHEN Zhihua,WANG Kai,et al.Research and progress on CA motar of ballastless slab track cushion[J].Journal of East China Jiaotong University,2009,26(4):59-62.
(中、英文编辑:付国彬)
Detection of Ballastless Track Diseases in High-Speed Railway Based on Ground Penetrating Radar
LIAO Hongjian1, ZHU Qingnü1, ZAN Yuewen2, XIE Yongyong1, SUN Junyu1
(1.School of Human Settlement and Civil Engineering,Xi'an Jiaotong University,Xi'an 710049,China;2.School of Geosciences and Environmental Engineering,Southwest Jiaotong University,Chengdu 610031,China)
A two-dimensional forward simulation was conducted to analyze slab ballastless track diseases in high-speed railway using the ground penetrating radar(GPR)technique.Based on the finite difference method,a two-dimensional forward simulation equation for GPR was deduced.By considering the different filling degrees and hardening progress of CA mortar layer,GPR geoelectric models for CRTS Ⅱ slab ballastless track were established and forward simulated,and the GPR picture features of the forward simulation were analyzed.The simulation results show that the forward simulation can clearly identify the interfaces between different dieletric layers and the number and location of reinforcement in slab ballastless track.
traffic engineering;high-speed railway;ballastless track;roadbed disease;ground penetrating radar;forward numerical simulation
U216.3
A
0258-2724(2016)01-0008-06
10.3969/j.issn.0258-2724.2016.01.002
2015-04-03
国家自然科学基金资助项目(41172276,51279155)
廖红建(1962—),女,教授,博士,博士生导师,研究方向为岩土工程数值分析,E-mail:hjliao@mail.xjtu.edu.cn
廖红建,朱庆女,昝月稳,等.基于探地雷达的高铁无砟轨道结构层病害检测[J].西南交通大学学报,2016,51(1):8-13.

