一类新的（k＋2，k）Hadamard MSR码

张司娜， 唐小虎， 李 杰

（西南交通大学信息科学与技术学院，四川成都610031）

一类新的（k＋2，k）Hadamard MSR码

张司娜， 唐小虎， 李 杰

（西南交通大学信息科学与技术学院，四川成都610031）

为降低分布式存储系统中节点的存储量，构造了一类新（k＋2，k）Hadamard MSR码．该码的每个编码矩阵皆对应于2个值，供其对角元素选取．在编码矩阵中，这2个值循环出现，且不同的矩阵，循环出现的周期不同．基于这一特性构造了节点的修复方案，将失效节点中的α个数据分成α／2组，每一组重建2个数据，其他k＋1个节点为每一组各提供1个数据．证明了若新码编码矩阵的对角元素可取的2个值不相等，则可最优修复系统节点；若所有编码矩阵对角元素可取的2个值的和为同一不为0的值，则可最优修复第1个校验节点；若所有编码矩阵对角元素可取的2个值的逆的和为1，则可最优修复第2个校验节点．新码的节点存储量降低到了Hadamard MSR码的理论界，可最优修复任意系统节点和1个校验节点．

分布式；存储；再生码；MSR码；高码率；最优；修复

分布式存储系统利用大量节点提供海量数据的存储服务，具有成本低、易扩展等优点，在云计算、云存储等有着广泛的应用，如OceanStore［1］、Total Recall［2］、DHash＋＋［3］．

为了保证数据的可靠性和可用性，分布式存储系统必须保持一定的数据冗余．纠删码就是一种重要的冗余存储机制，其磁盘利用率高．现有采用纠删码方案的分布式存储系统有Facebook的Hadoop、Google Colossus与Microsoft Azure［4］．

基于纠删码，将一个大小为M＝kα的文件编码成同样大小的n份（大小为α），任意k份都可恢复出原文件，即具有MDS（maximum distance separable）性质．在纠删码中，节点中的数据被视为标量，所以，当一个节点失效，为修复其数据（大小为α），需要从其他k个节点下载其全部数据，换言之，为修复M／k个数据，纠删码需要下载M个数据．

近年来，文献［5］提出了最小存储再生（minimum storage regenerating，MSR）码，该码具有MDS性质，磁盘利用率与纠删码相同．该码将节点中的数据视为矢量，在修复失效节点的M／k个数据时，从其他d个（d≥k）可用节点下载其部分数据［6］，下载的数据总量（称为修复带宽）为dM／k（d－k＋1）＜M．

（n＝k＋2，k）系统MSR码具有以下优势：

（1）重建原文件时，若选取系统节点，无需计算；

（2）与其他MSR码相比，存储开销最小［7-8］．

现有的（n＝k＋2，k）系统MSR码见文献［9-15］．其中，文献［9］提出的Hadamard MSR码的系统节点与校验节点中的同一层数据恰好组成一个标量MDS码．这一特性不仅使得Hadamard MSR码可直接用于基于纠删码的分布式存储系统，而且当某一系统节点中的数据变更时，所有校验节点只需变更同层的数据，即具有最优更新性质．

文献［16］证明了（k＋2，k）Hadamard MSR码的节点存储量α的下界为2k，然而，文献［9］提出的Hadamard MSR码的节点存储量α＝2k＋1，是下界的2倍．

本文构造了一个新的（k＋2，k）Hadamard MSR码．新码的节点存储量α达到了理论界2k，具有最优更新性质，可最优修复所有系统节点，虽然只能最优修复一个校验节点，但对整个系统性能的影响较小，系统节点数远大于2，其失效概率远大于校验节点，而且与校验节点相比，系统节点的失效更严重，因为后者导致原始数据的丢失，增大用户访问信息的时恒．

1 （k＋2，k）Hadamard MSR码的结构与修复特性

在域Fq上，用（k＋2，k）系统MSR码对一个大小为M＝kα的文件进行编码，生成k＋2份大小均为α的数据．其中，k份包含的是原始数据，另2份是原始数据的线性表达．这k＋2份数据分别存储于k＋2个存储节点．存储原始数据的节点称为系统节点，其他存储节点称为校验节点．若将节点i（1≤i≤k＋2）中的数据用一个α维列向量ci表示，

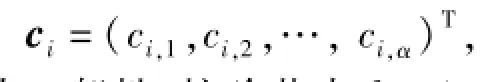
不失一般性，校验节点k＋1中的数据可表示为所有系统节点中的数据之和，即

校验节点k＋2中的数据可表示为所有系统节点中数据的线性组合，即

其中，Ai（1≤i≤k）是α×α的矩阵，称为系统节点i的编码矩阵．若该系统MSR码选用（k＋2，k）Hadamard MSR码，编码矩阵A1，A2，…，Ak均为对角矩阵，其编码矩阵Ai（1≤i≤k）可表示为

其中，ai，l∈Fq，1≤l≤α．（k＋2，k）Hadamard MSR码的结构如表1所示．

由表1可以看出，在（k＋2，k）Hadamard MSR码中，校验节点中的数据仅与系统节点中同层的数据相关，而与其他层的数据无关．因而，在某一系统节点中的数据变更时，所有校验节点只需变更同层的数据，换言之，（k＋2，k）Hadamard MSR码具有最优更新性质．由表1还可以看出，在每一层，（c1，l，…，ck，l，ck＋1，l，ck＋2，l）均是一个（k＋2，k）标量MDS码，1≤l≤α，所以，（k＋2，k）Hadamard MSR码可看作α层标量MDS码的组合．显然，若（k＋2，k）Hadamard MSR码具有MDS性质，需要编码矩阵的对角元素满足ai，l≠0与ai，l－aj，l≠0，其中，1≤i≠j≤k，1≤l≤α．

表1 （k＋2，k）Hadamard MSR码的结构Tab．1 Structure of（k＋2，k）Hadamard MSR code

在（k＋2，k）Hadamard MSR码中，失效节点的最优修复是分组进行、同层相助的［17］．在另外k＋1个节点的帮助下，失效节点中数据（大小为α）的修复是分成α／2组并行进行的，每一组负责重建2个数据，若失效节点的第l层与第s层（l≠s）的数据分为一组进行修复，为重建这2个数据，每一个帮助节点提供的数据（大小为1）也是由各自的第l层与第s层数据生成的．

2 一类新的（k＋2，k）Hadamard MSR码

文献［9］提出的（k＋2，k）Hadamard MSR码的节点存储量α为2k＋1，是文献［16］给出的理论界的2倍．为降低节点存储量，本文对其进行了改进，构造了一类新的（k＋2，k）Hadamard MSR码．新码的节点存储量α为2k，降低到了理论界．

（k＋2，k）MSR码由编码矩阵A1，A2，…，Ak组成，而（k＋2，k）Hadamard MSR码的编码矩阵均为对角阵．

在新（k＋2，k）Hadamard MSR码中，编码矩阵Ai（1≤i≤k）主对角线上的元素ai，l（1≤l≤α＝2k＋1）取值为

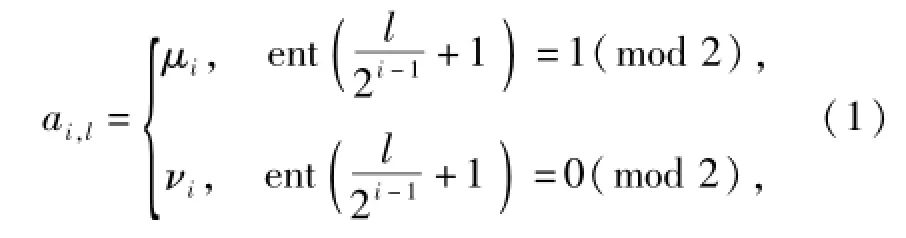
即，编码矩阵

为方便后续定理的证明，将新码编码矩阵对角元素的取值规律以引理的形式表示．

引理1 ai，l＝ai，l＋2i－1，aj，l与aj，l＋2i－1一个取μi，另一个取νi，其中，1≤i≠j≤k，l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1．

证明 根据式（1），引理1等价于

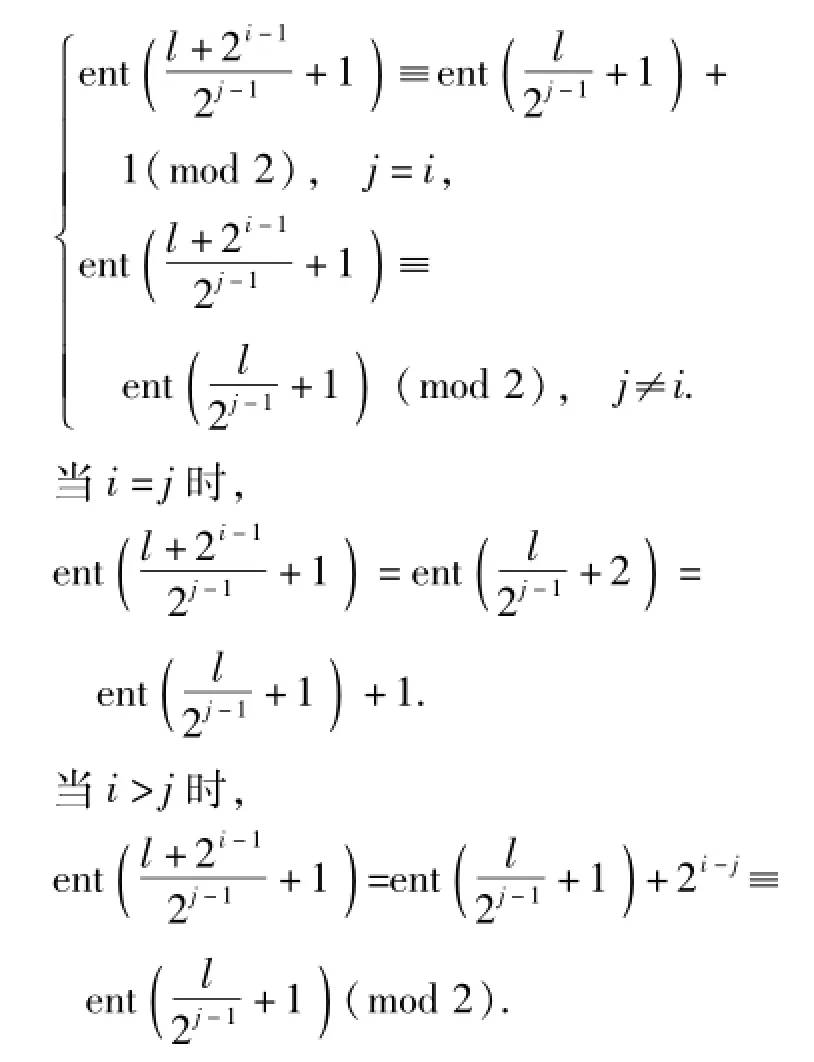
当i＜j时，不失一般性，令

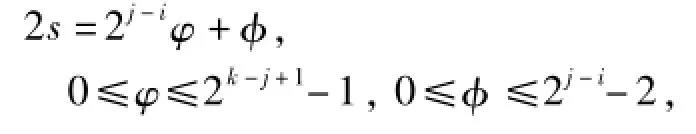
则有

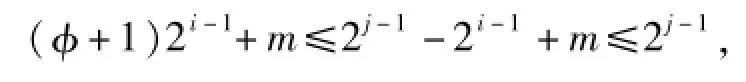
而

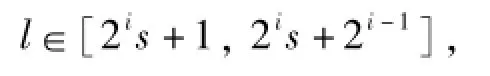
则有

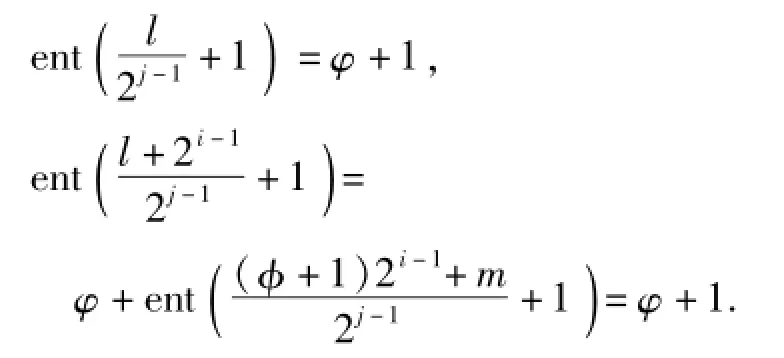
引理2 ai，l与ai，2k－l＋1一个取μi，另一个取νi，其中，1≤i≤k，l∈［1，2k－1］．证明 不失一般性，令

则

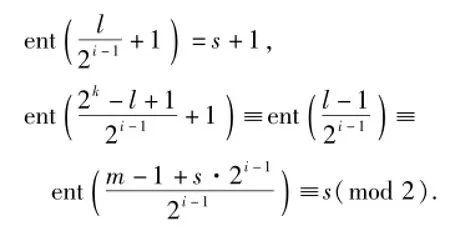
根据式（1），ai，l与ai，2k－l＋1一个取μi，另一个取νi．

2．1 系统节点的最优修复方案

在新（k＋2，k）Hadamard MSR码中，系统节点i（1≤i≤k）的修复是将第l层（l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1）与第l＋2i－1层分为一组，为修复该组数据，其他系统节点与校验节点提供的数据均是这2层的数据之和．

下面证明编码矩阵的对角元素的取值μi与νi（1≤i≤k）满足何种条件时，新（k＋2，k）Hadamard MSR码可最优修复系统节点．

定理1 若μi≠νi（1≤i≤k），新（k＋2，k）Hadamard MSR码可最优修复所有系统节点．

证明 系统节点i（1≤i≤k）中的数据为ci，1，ci，21，…，ci，2k，为重建ci，l与ci，l＋2i－1（l∈［2is＋1，2is＋2i－1］，0≤s≤2k－i－1），从其他系统节点下载

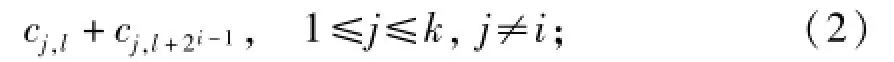
从校验节点k＋1下载ck＋1，l＋ck＋1，l＋2i－1，即为

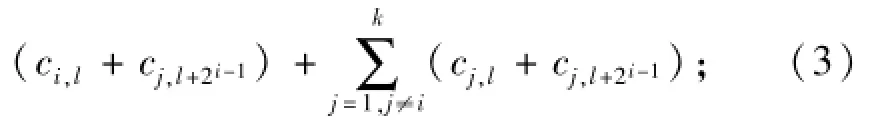
从校验节点k＋2下载ck＋2，l＋ck＋2，l＋2i－1，即为

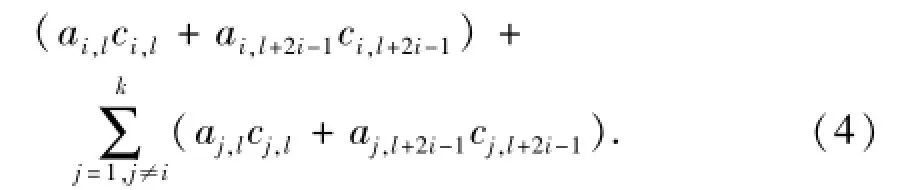
由引理1可知，aj，l＝aj，l＋2i－1，因而，式（3）与式（4）的最后一项都可由式（2）消去，而式（3）的第1项与式（4）的第1项组成关于ci，l与ci，l＋2i－1的方程组，只要ai，l≠aj，l＋2i－1，该方程组可解．

由引理1知，ai，l与aj，l＋2i－1一个取μi，另一个取νi，所以，只要μi≠νi，则可解出ci，l与ci，l＋2i－1．

因此，若μi≠νi（1≤i≤k），新（k＋2，k）Hadamard MSR码可最优修复所有系统节点．

2．2 校验节点的最优修复

新（k＋2，k）Hadamard MSR码无法保证2个校验节点均可最优修复，只能选取一个进行最优修复．

若可最优修复校验节点k＋1，其修复是将第l层（l∈［1，2k－1］）与第2k－l＋1层分为一组．为修复该组数据，系统节点提供的数据是这2层数据之和，而校验节点k＋2提供的则是这2层数据之差．

下面证明编码矩阵对角元素的取值μi与νi（1≤i≤k）满足何种条件时，新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋1．

定理2 若μ1＋ν1＝μ2＋ν2＝…＝μk＋νk≠0，新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋1．

证明 校验节点k＋1中的数据为ck＋1，1，ck＋1，21，…，ck＋1，2k，为重建ck＋1，l与ck＋1，2k－l＋1（l∈［1， 2k－1］），从k个系统节点下载

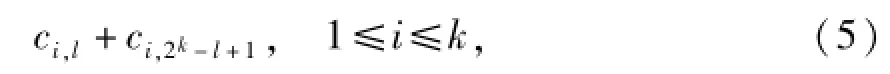
将式（5）的所有项相加，得

从校验节点k＋2下载ck＋2，l－ck＋2，2k－l＋1，即为

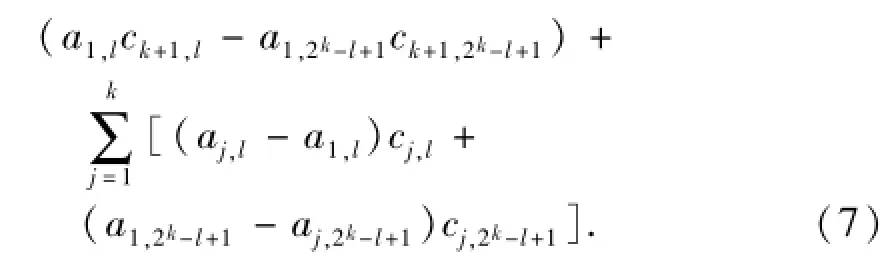
式（6）与式（7）组成关于ck＋1，l与ck＋1，2l－l＋1的方程组，若要方程组可解，需要a1，l＋a1，2k－l＋1≠0并且式（7）的最后一项可消去，即

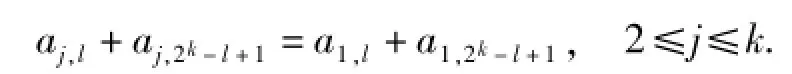
由引理2可知，ai，l与ai，2k－l＋1一个取μi，另一个取νi，即

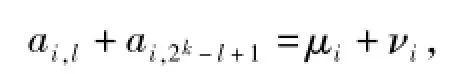
那么，只要

则可解出ck＋1，l与ck＋1，2l－l＋1．

因此，若

新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋1．

若新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋2，其分组与修复校验节点k＋1时相同，即第l层（l∈［1，2k－1］）与第2k－l＋1层分为一组．为修复该组数据，系统节点提供的数据是这2层的数据之和，而校验节点k＋1提供的则是这2层的数据之差．

下面证明编码矩阵的对角元素的取值μi与νi（1≤i≤k）满足何种条件时，新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋2．

定理3 若μ－1i＋ν－1i＝1（1≤i≤k），新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋2．

证明 校验节点k＋2中的数据为ck＋2，1，ck＋2，21，…，ck＋2，2k，为重建ck＋2，l与ck＋2，2k－l＋1（l∈［1，2k－1］），从k个系统节点下载

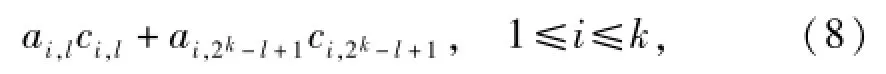
将式（8）的所有项相加，得

从校验节点k＋1下载ck＋1，l－ck＋1，2k－l＋1，即为

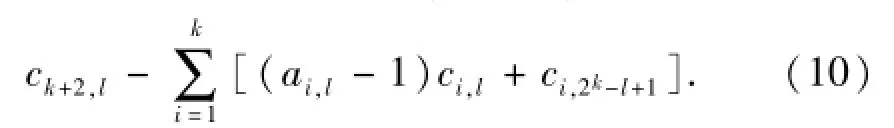
式（9）与式（10）组成关于ck＋2，l与ck＋2，2k－l＋1的方程组，若要方程组可解，式（10）的最后一项需消去，即需

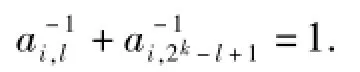
由引理2可知，ai，l与ai，2k－l＋1一个取μi，另一个取νi，即

那么，只要

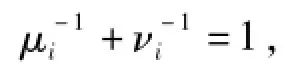
则可解出ck＋2，l与ck＋2，2k－l＋1．

因此，若

新（k＋2，k）Hadamard MSR码可最优修复校验节点k＋2．

2．3 新码的M DS性质

下面证明编码矩阵的对角元素的取值μi与νi（1≤i≤k）满足何种条件时，新（k＋2，k）Hadamard MSR码满足MDS性质．

定理4 若μi≠0，νi≠0，μi≠νi，μi≠μj，νi≠νj（1≤i≠j≤k），新（k＋2，k）Hadamard MSR码具有MDS性质．

证明 若（k＋2，k）Hadamard MSR码具有MDS性质，需要编码矩阵的对角元素满足ai，l≠0与ai，l－aj，l≠0（1≤i≠j≤k，1≤l≤α）．由式（1）知，新码的ai，l取值μi或νi，则ai，l－aj，l的取值有4种，分别为μi－μj，νi－νj，μi－μj，νi－νj那么，若要ai，l≠0与ai，l－aj，l≠0同时成立，则需μi≠0，νi≠0，μi≠νj，μi≠μj，νi≠νj．

因此，若μi≠0，νi≠0，μi≠νj，μi≠μj，νi≠νj（1≤i≠j≤k），新（k＋2，k）Hadamard MSR码具有MDS性质．

下面确定新（k＋2，k）Hadamard MSR码需要多大的域．综上所述，新码若可最优修复所有系统节点且具有MDS性质，需要

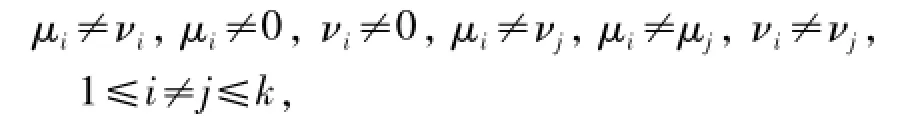
即要求μi，νi（1≤i≤k）为2k个不相同的非零数．而

（可最优修复校验节点k＋1的充分条件）与

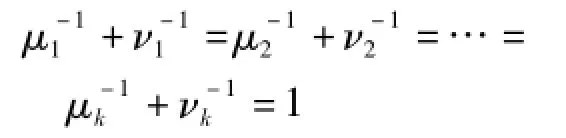
（可最优修复校验节点k＋2的充分条件）均要求μi与νi（1≤i≤k）是k对和相同且和不为0的数．因此，新（k＋2，k）Hadamard MSR码需要有限域Fq具有奇特征且q≥2k＋3．

在域Fq（q≥2k＋3）上，若新码选择最优修复校验节点k＋1，μi与νi（1≤i≤k）可取

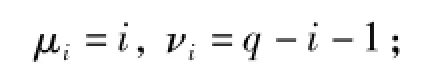
若选择最优修复校验节点k＋2，μi与νi（1≤i≤k）可取

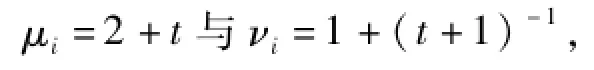
其中，1≤t≤q－2．

3 结 论

本文给出了一类新的（k＋2，k）Hadamard MSR码，其节点存储量达到了Hadamard MSR码的理论界．给出了节点的分组修复方案，基于该修复方案，证明了新码可最优修复系统节点与校验节点的充分条件．

［1］ RHEA S，WELLS C，EATON P，et al．Maintenancefree global data storage［J］．IEEE Internet Computing，2001，5（5）：40-49．

［2］ BHAGWAN R，TATI K，CHENG Y C，et al．Total recall：System support for automated availability management［C］∥Symposium Networked Systems Design and Imp lementation．San Francisco：ACM，2004：25-25．

［3］ DABEK F，LIJinyang，SIT E，etal．Designing a DHT for low latency and high throughput［C］∥Symposium Networked Systems Design and Implementation（NSDI）．San Francisco：ACM，2004：85-98

［4］ HUANG Cheng，SIMITCI H，XU Yi，et al．Erasure coding in windows azure storage［C］∥Usenix annual Technical Conference．Boston：ACM，2012：15-26．

［5］ DIMAKISA G，GODFREY P B，WU Yunnan，et al．Network coding for distributed storage systems［J］．IEEE Transactions on Information Theory，2010，56（9）：4539-4551．

［6］ 范文礼，刘志刚．基于传输效率矩阵的复杂网络节点重要度排序方法［J］．西南交通大学学报，2014，49（2）：337-342．FAN Wenli，LIU Zhigang．Ranking method for node importance based on efficiency matrix［J］．Journal of Southwest Jiaotong University，2014，49（2）：337-342．

［7］ DIMAKISA G，RAMCHANDRAN K，WU Yunnan，et al．A survey on network codes for distributed storage［J］．Proceedings of the IEEE，2011，99（3）：476-489．［8］ 郝杰，逯彦博，刘鑫吉，等．分布式存储中的再生码综述［J］．重庆邮电大学学报：自然科学版，2013，25（1）：30-38．HAO Jie，LU Yanbo，LIU Xinji，et al．Survey for regenerating codes for distributed storage［J］．Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition，2013，25（1）：30-38．

［9］ PAPAILIOPOULOS D S，DIMAKIS A G，CADAMBE V R．Repair optimal erasure codes through hadamard designs［J］．IEEE Transactions on Information Theory，2013，59（5）：3021-3037．

［10］ TAMO I，WANG Zhiying，BRUCK J．Zigzag codes：MDS array codes with optimal rebuilding［J］．IEEE Transactions on Information Theory，2013，59（3）：1597-1616．

［11］ WANG Zhiying，TAMO I，BRUCK J．Long MDS codes for optimal repair bandwidth［C］∥Proceedings of IEEE International Symposium on Information Theory．Cambridge：IEEE，2012：1182-1186．

［12］ TAMO I，WANG Zhiying，BRUCK J．MDS array codes with optimal rebuilding［C］∥Proceedings of IEEE International Symposium on Information Theory．St．Petersburg：IEEE，2011：1240-1244．

［13］ CADAMBE V R，JAFAR S A，MALEKI H，et al．Asymptotic interference alignment for optimal repair of MDS codes in distributed storage［J］．IEEE Transactions on Information Theory，2013，59（5）：2974-2987．

［14］ CADAMBE V R，HUANG Cheng，LI Jin，et al．Polynomial length MDS codes with optimal repair in distributed storage［C］∥The 45th Asilomar Conference on Signals，Systems and Computers（ASILOMAR）．Pacific Grove：IEEE，2011：1850-1854．

［15］ CADAMBE V R，HUANG Cheng，LI Jin．Permutation code：Optimal exact-repair of a single failed node in MDS code based distributed storage systems［C］∥Proceedings of IEEE International Symposium on Information Theory Proceedings（ISIT）．St．Petersburg：IEEE，2011：1225-1229．

［16］ TAMO I，WANG Zhiying，BRUCK J．Access versus bandwidth in codes for storage［J］．IEEE Transactions on Information Theory，2014，60（4）：2028-2037．

［17］ TANG Xiaohu，YANG Bin，LI Jie．New repair strategy of hadamard minimum storage regenerating code for distributed storage system［J／OL］．（2013-12-18）［2014-12-10］．http：／／arxiv．org／pdf／1312．5173v1．pdf．

（中文编辑：唐 晴 英文编辑：周 尧）

A New（k＋2，k）Hadamard Minimum Storage Regenerating Code

ZHANG Sina， TANG Xiaohu， LI Jie
（School of Information Science and Technology，Southwest Jiaotong University，Chengdu 610031，China）

To reduce the storage capacity of nodes in distributed storage systems，a new（k＋2，k）Hadamard Minimum Storage Regenerating（MSR）code was constructed．Each coding matrix is related to two values，from which the diagonal elements of this coding matrix are selected．These two values appear in the coding matrix in a repeating pattern，but with different repeating cycles for different matrices．Based on the structure of the coding matrix，a repair strategy was constructed．The repair strategy divides symbols in the failed node intoα／2 groups with two symbols in each group，then the two symbols are recovered by downloading one symbol from each of the other k＋1 nodes．If the two values related to each coding matrix are unequal，the new Hadamard MSR code can optimally repair systematic nodes．If the sum of two values related to each coding matrix is nonzero and the k values are the same，the new Hadamard MSR code can optimally repair the first parity node．If the sum of the inverse of two values related to each coding matrix is one，the new Hadamard MSR code can optimally repair the second parity node．The new code reduces the storage capacity to the bond for Hadamard MSR code．Further，it can optimally repair all systematic nodes and one parity node．

distributed；storage；regenerating code；MSR code；high code-rate；optimal；repair

TN911．22

A

0258-2724（2016）01-0188-06 DO I：10．3969／j．issn．0258-2724．2016．01．026

2015-02-01

张司娜（1985—），女，博士研究生，研究方向为分布式存储编码，E-mail：nsz1221＠163．com

唐小虎（1971—），男，教授，博士生导师，研究方向为信息安全与编码，E-mail：xhtang_scce＠home．swjtu．edu．cn

张司娜，唐小虎，李杰．一类新的（k＋2，k）Hadamard MSR码［J］．西南交通大学学报，2016，51（1）：188-192，200．