无砟轨道层间裂纹内动水压力特性分析

曹世豪， 杨荣山， 刘学毅， 苏成光， 郭利康

（西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031）

无砟轨道层间裂纹内动水压力特性分析

曹世豪， 杨荣山， 刘学毅， 苏成光， 郭利康

（西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031）

在雨水丰富和排水不畅的地区，水对无砟轨道层恒裂纹扩展的影响比较突出．为研究高速列车作用下无砟轨道裂纹内水压力的分布规律及压力大小的影响因素，基于质量守恒和动量定理，采用控制体积法，导出了裂纹内动水压力分布解析式．应用有限元分析软件ANSYS和CFX，分析了荷载频率、荷载幅值、裂纹深度、裂纹开口量等对动水压力的影响．分析结果表明：沿着裂纹出口的方向，水压力呈减小趋势，其最大值发生在裂纹尖端处；动水压力与荷载频率近似呈二次方关系，与荷载幅值呈线性关系，与裂纹开口量呈一次反比关系．在幅值为10 kN、频率为5 Hz荷载作用下，水压力分布的试验测试结果与理论分析基本一致，两种方法获得的水压力峰值分别为0．177、0．161 kPa．

无砟轨道；裂纹；列车；荷载；水压力

无砟轨道服役过程中混凝土内或层恒出现裂纹较为普遍，这些裂纹在降雨量较少地区扩展相对缓慢，而在雨水丰富或排水不畅地段扩展速率要快得多［1-4］．可见，水在无砟轨道裂纹扩展过程中起着极为重要的作用．

由于水压力产生和作用机理的复杂性，目前国内外在无砟轨道领域对相关问题仅有初步的研究．徐桂弘通过试验对荷载幅值对水压力的影响进行了分析［3］；颜华对静水作用下CA砂浆力学性能变化进行了研究［4］．类似的研究也集中于混凝土重力坝领域，徐世烺和Saouma通过机械荷载与静水压力耦合作用下的水力劈裂试验研究表明，裂纹内的静水压力会降低结构的承载能力［5-9］；Tinawi对不同频率的地震荷载作用下混凝土重力坝裂缝内水压力进行研究，认为高频荷载产生的水压力较大［10-11］．上述研究多是基于静水压力作用，而仅有的少量动水压力研究难以反映无砟轨道承受荷载大、频率高的作用特点．

本文基于质量守恒和动量定理，采用控制体积法推导出高速列车荷载作用下无砟轨道层恒裂纹内动水压力分布解析式，应用有限元分析软件ANSYS和CFX，分析荷载频率、荷载幅值、裂纹深度、裂纹开口量等对动水压力的影响，明确动水压力产生与作用机理，为进一步分析无砟轨道伤损及其发展过程提供依据．

1 无砟轨道层间裂纹内动水压力产生机理及计算模型

1．1 动水压力产生与作用机理

无砟轨道层恒裂纹随着列车的趋近与离开而发生周期性的张开与闭合．加载时，由于裂纹面的相互靠近，使得裂纹内水被排出，此时裂纹内产生正压力，并沿着出口方向呈减小趋势，其最大值发生在裂纹尖端处；卸载时，由于裂纹面的相互远离，使得裂纹外水被吸回裂纹内，此时裂纹内产生负压力，并沿着出口方向呈增加趋势，其最小值发生在裂纹尖端处，如图1所示．

图1 无砟轨道裂纹内水的流动和压力分布Fig．1 Water flow and pressure distribution in crack of the ballastless track

在列车荷载作用下，裂纹内部的水会产生一定的压力和速度，并对裂纹表面进行反复的冲刷，在裂纹出口处形成冒浆现象，如图2（a）所示；之后，经过长期的列车荷载与水的耦合作用，支承层与轨道板恒缝隙逐渐增大，导致轨道板底被掏空，如图2（b）所示；此外，产生的动水压力垂直作用于裂纹表面，成为裂纹扩展的驱动力，加速裂纹的扩展．

图2 轨道板底冒浆和脱空Fig．2 Slurry and hollowed-out under the track slab

1．2 计算模型

CRTSⅡ型板式无砟轨道由钢轨、弹性扣件、预制轨道板、砂浆调整层及支承层等构成，如图3所示．本文假定裂纹位于支承层与砂浆调整层界面处，其中裂纹深度为L（0．2～1．2 m），开口量为h（1～5 mm）；裂纹内充满水，忽略水的压缩性，荷载平均施加在承轨台上，在不考虑弹性基础的影响下，底部采取全约束；相关计算参数如表1所示［3，12-13］．

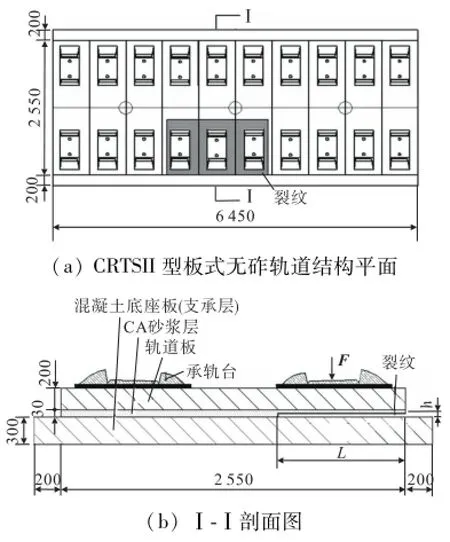
图3 计算模型Fig．3 Calculation model

表1 计算参数Tab．1 Calculation parameters

续 表1

2 裂纹内动水压力计算公式推导

采用控制体积法时，不可压缩流体的质量守恒定律积分表达式［10］为

不可压缩流体的动量定理积分表达式为

式中：m为控制体的质量；ρ为控制体的密度；A为控制体的面积；L为控制体边界；u为速度矢量；n为控制体边界的外法线方向；M为控制体的动量；F为作用在控制体上的力矢量．

在线弹性范围内，结构的位移与荷载大小成线性关系［14］；据此，亦假设图4所示裂纹的上表面位移y与荷载大小成线性关系，则x处的裂纹开口量ωx为

式中：β（x）为变形系数．

图4 裂纹变形示意图（放大）Fig．4 Deformation diagram of crack（amplification）

考虑流体黏性，假设裂纹内水的速度分布（vx，y）呈抛物线形，即符合泊肃叶流动［10，15］，则：

选择图4所示的控制体1（0～x恒流体域），其中v0，y＝0，将式（3）、（4）代入式（1）中，并化简得：

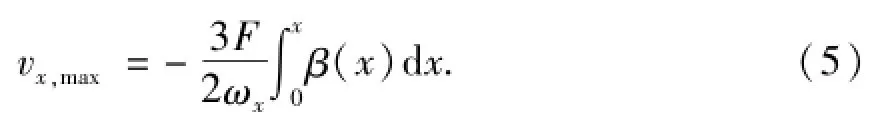
选择图4所示的控制体2（x～L恒流体域），其受力示意图如图5所示．

图5 控制体受力示意图Fig．5 Forces acting on the control volume

图5 中，τx，FSI为流体对固体边界处的剪应力；pη、px为横坐标η、x处的水压力；pL为裂纹出口处水的绝对压强．

由牛顿内摩擦定律可知，流体的黏滞切应力τ与速度梯度成正比［13］，即：

式中：μ为动力黏滞系数．

结合式（4）求得控制体所受合力沿x方向的分力为

将式（3）、（5）、（7）代入到式（2）中，并化简得：

式中：

式（8）即为列车荷载作用下无砟轨道层恒裂纹内动水压力分布解析式．

3 动水压力解析式备项影响分析

3．1 公式简化

当裂纹上表面位移量远小于裂纹开口量时，在式（9）所示正弦荷载作用下，裂纹内动水压力计算式（8）可化为式（10）所示形式：

式中：Fm为荷载平均值；Fo为荷载幅值；f为荷载频率．

其中A项是由控制体恒的相互挤压而产生的，B项由裂纹上表面的变形导致开口量变化而产生，C项是由流体黏性作用而产生的．当y≪h时，因裂纹变形导致开口量变化而造成的压力变化量是很微小的，此时B项对裂纹内动水压力的影响可忽略不计．

3．2 流体黏性的影响

为了进一步研究式（10）中A项和C项的主次作用关系，假定RCA为C项最大值与A项最大值的比，则：

从式（11）可知，在流体性质确定不变时，RCA受到荷载频率和裂纹开口量的共同影响；随着加载频率和裂纹开口量的增加，黏性的影响均逐渐降低．通过式（11）分别计算10、20、30 Hz荷载作用下RCA随裂纹开口量的变化关系，如图6所示．由此可知，对于高频列车荷载作用下的无砟轨道层恒裂纹，当裂纹开口量大于2 mm时，流体黏性对动水压力的影响是很微小的，此时动水压力主要由解析式的A项所决定，即水压力大小与加载频率呈二次方关系，与加载幅值呈线性关系，与裂纹开口量成一次反比关系．

图6 流体黏性的影响Fig．6 Effect of the fluid viscosity

4 动水压力试验验证

动水压力试验系统主要由水槽、含裂纹混凝土试件、加载系统、水压力传感器及数据采集系统组成．试件尺寸见图7，其裂纹深度为0．25 m，开口量为3 mm．混凝土等级为C30，弹性模量为30 GPa，泊松比为0．2．水槽中注入20℃的水，水位淹没压力传感器．荷载由250 kN万能伺服液压疲劳试验机施加，荷载为25±10 kN，频率为5 Hz，荷载形式为正弦．裂纹内的水压力通过高精度数字压力传感器（PT1、PT2、PT3）测量，传感器的测量精度为1 Pa，采样恒隔为10 ms．通过试验测量及理论计算求得的裂纹内水压力分布见图8．

图7 试验装置（单位：cm）Fig．7 Experimental setup（unit：cm）

图8 裂纹内水压力分布Fig．8 Distribution of water pressure in the crack

通过比较图8中的实验测试和理论计算结果可知，水压力分布实验测试结果和理论计算结果有很好的一致性，因此，可以认为本文推导的动水压力公式基本是正确的．

5 无砟轨道层间裂纹内动水压力特性分析

5．1 有限元模型

根据前面提出的计算模型（见图3），应用ANSYS与CFX进行瞬态流固耦合分析，分析加载频率、加载幅值、开口量、裂纹深度等因素对动水压力的影响．计算模型的整体与局部有限元网格如图9所示，其中远离裂纹区域的单元尺寸为10 mm，裂纹附近区域及流体域单元尺寸为0．5 mm；整个模型的单元数为66 002个，节点数为73 027个．

图9 有限元模型Fig．9 Finite element model

5．2 结果及分析

5．2．1 荷载频率的影响

深为1 m、开口量为3 mm的无砟轨道裂纹，在幅值为75 kN的不同频率（10、15、20、25、30、35、40 Hz）荷载作用下，裂纹内水压力分布及水压力峰值随荷载频率的变化如图10所示．

图10 荷载频率对水压力的影响Fig．10 Effect of the loading frequency on water pressure

由图10（a）和图10（b）可知，水压力沿着裂纹呈减小趋势，其最大值发生在裂纹尖端处；水压力的分布规律可从质量守恒和动量定理的角度来解释；当裂纹面挤压流体时，由流体质量守恒可知，沿着裂纹出口方向流体速度会逐渐增加，即速度呈增加趋势；控制体速度的增加亦表示动量的增加，根据动量定理，控制体所受合力方向与动量增加的方向一致，由此可见，水压力沿着裂纹出口方向呈减小趋势．由图10（c）可知，动水压力随着荷载频率的增加而增加，且水压力与荷载频率基本呈二次方关系．

5．2．2 荷载幅值的影响

深为1 m，开口量为3 mm的无砟轨道裂纹，在频率为30 Hz的不同幅值（60、75、80、100 kN）荷载作用下，裂纹内水压力分布及水压力峰值随荷载幅值的变化如图11所示．

图11 荷载幅值对水压力的影响Fig．11 Effect of the load amplitude on water pressure

由图11（a）和图11（b）可知，无砟轨道裂纹内动水压力沿着裂缝呈减小趋势，其最大值发生在裂纹尖端处．由图11（c）可知，解析计算与数值模拟基本一致，即水压力随着荷载幅值的增加而增加，且动水压力与荷载幅值基本呈线性关系．

5．2．3 裂纹开口量的影响

深为1 m，不同开口量（1．0、1．5、2．0、3．0、4．0、5．0 mm）的无砟轨道裂纹，在幅值为75 kN、频率为30 Hz的荷载作用下，裂纹内水压力分布及水压力峰值随裂纹开口量的变化如图12所示．

图12 裂纹开口量对水压力的影响Fig．12 Effect of the crack opening on water pressure

由图12（a）和图12（b）可知，无砟轨道裂纹内水压力沿着裂纹呈减小趋势，其最大值发生在裂纹尖端处．由图12（c）可知，解析计算与数值模拟基本一致，即水压力随着裂纹开口量的增加而减小；且动水压力与裂纹开口量呈一次反比关系．

5．2．4 裂纹深度的影响

开口量为3 mm，不同深度（0．2、0．4、0．6、0．8、1．0、1．2 m）的无砟轨道层恒裂纹，在幅值为75 kN、频率为30 Hz的荷载作用下，裂纹内水压力分布及水压力峰值随裂纹深度的变化见图13．

图13 裂纹深度对水压力的影响Fig．13 Effect of the crack length on water pressure

由图13（a）和图13（b）可知，无砟轨道层恒裂纹内水压力沿着裂纹呈减小趋势，其最大值发生在裂纹尖端处．由图13（c）可知，解析计算与数值模拟基本一致，即水压力随着裂纹深度的增加而增加；当裂纹深度小于0．4 m时，产生的水压力比较小，此时水压力对结构的水力劈裂作用基本可忽略不计；当裂纹深度大于0．4 m后，水压力随着裂纹深度的增加而急速增加，产生的水压力垂直作用于裂纹表面，当尖端的应力强度因子超出材料的断裂韧性时，发生水力劈裂，使结构瞬恒破坏．

综合上述研究，对于列车荷载作用下，在裂纹形状保持不变时，列车行车速度和轴重是影响无砟轨道裂纹内水压力的两个重要因素，水压力随着列车行车速度与轴重的增大而增加，且与行车速度基本呈二次方关系，与轴重呈线性关系．

6 结 论

针对高频列车荷载作用下，无砟轨道层恒裂纹内水压力分布问题，通过理论分析、试验研究、数值模拟，得出以下结论：

（1）考虑流体的黏性，基于质量守恒和动量定理，采用控制体积法导出列车荷载作用下无砟轨道层恒裂纹内水压力分布解析式；通过试验验证表明，理论计算与试验测试结果基本一致．

（2）列车荷载作用下，无砟轨道层恒裂纹内动水压力是由流体黏性、裂缝开口量、荷载频率和荷载幅值等因素综合决定的；当裂纹开口量大于2 mm时，流体黏性的影响基本可忽略不计，此时水压力大小与荷载频率呈二次方关系，与荷载幅值呈线性关系，与裂纹开口量呈一次反比关系；数值模拟与理论分析基本一致．

（3）裂纹内水压力沿着裂纹出口方向呈减小趋势，最大值发生在裂纹尖端处．

［1］ 王平，徐浩，陈嵘，等．路基上CRTSⅡ型板式轨道裂纹影响分析［J］．西南交通大学学报，2012，47（6）：929-934．WANG Ping，XU Hao，CHEN Rong，et al．Effects analysis of cracking of CRTS Ⅱ slab track on subgrade［J］．Journal of Southwest Jiaotong University，2012，47（6）：929-934．

［2］ 任娟娟，严晓波，徐光辉，等．底座板脱空对板式无砟轨道行车动力特性的影响［J］．西南交通大学学报，2014，49（6）：951-966．REN Juanjuan，YAN Xiaobo，XU Guanghui，et al．Effect of contact loss underneath concrete roaded on dynamic performances of slab Track-subgrade system［J］．Journal of Southwest Jiaotong University，2014，49（6）：951-966．

［3］ 徐桂弘，杨荣山，刘学毅．荷载幅值对无砟轨道结构裂纹水压力影响［J］．铁道工程学报，2015（1）：32-37．XU Guihong，YANG Rongshan，LIU Xueyi．Impact of load amplitude on the water pressure of non-ballasted track structure［J］．Journal of Railway Engineering Society，2015（1）：32-37．

［4］ 颜华，胡华锋，曾晓辉，等．静水作用下板式无砟轨道CA砂浆力学性能变化［J］．高速铁路技术，2014，5（4）：10-14．YAN Hua，HU Huafeng，ZENG Xiaohui，et al．Studies on mechanical changes of CA mortar for slab track under hydrostatic effect［J］．High Speed Railway Technology，2014，5（4）：10-14．

［5］ 徐世烺，王建敏．静水压力下混凝土双K断裂参数试验测定［J］．水利学报，2007，38（7）：792-798．XU Shilang，WANG Jianmin．Experimental determination of double-K fracture parameters of concrete under water pressure［J］．Journal of Hydraulic Engineering，2007，38（7）：792-798．

［6］ BRHWILER E，SAOUMA V．Water Fracture interaction in concrete，partⅠ：racture properties［J］．ACI Materials Journal，1995，92（3）：296-303．

［7］ BRHWILER E，SAOUMA V．Water Fracture interaction in concrete，partⅡ：hydrostatic pressure in cracks［J］．ACI Materials Journal，1995，92（3）：383-390．

［8］ SLOWIK V，SAOUMA V．Water pressure in propagation concrete cracks［J］．Journal of Structural Engineering，2000，126（2）：235-242．

［9］ SHINMURA A，SAOUMA V．Fluid fracture interaction in pressurized reinforced concrete vessels［J］．Materials and Structures，1997，30（2）：72-80．

［10］ TINAWI R，GUIZANI L．Formulation of hydrodynamic pressure in cracks due to earthquakes in concrete dams［J］．Earthquake Engineering and Structural Dynamics，1994，23（7）：699-715．

［11］ JAVANMARD F，LEGER P，TINAWI R．Seismic structural stability of concrete gravity dams considering transient uplift pressures in cracks［J］．Engineering Structures，2005，27：616-628．

［12］ 中华人民共和国铁道部．铁建设［2005］754客运专线无砟轨道设计指南［S］．北京：中国铁道出版社，2005．

［13］ 陈长植．工程流体力学［M］．武汉：华中科技大学出版社，2008：104-105．

［14］ 吴家龙．弹性力学［M］．北京，高等教育出版社，2001：109-114．

［15］ 李宗利，任青文，王亚红．岩石与混凝土水力劈裂缝内水压力分布的计算［J］．水利学报，2005，36（6）：656-661．LI Zongli，REN Qingwen，WANG Yahong．Formula for water pressure distribution in rock or concrete fractures formed by hydraulic fracturing［J］．Journal of Hydraulic Engineering，2005，36（6）：656-661．

（中文编辑：唐 晴 英文编辑：周 尧）

Analysis of Water Pressure in Ballastless Track Crack

CAO Shihao， YANG Rongshan， LIU Xueyi， SU Chengguang， GUO Likang
（MOE Key Laboratory of High-Speed Railway Engineering，Southwest Jiaotong University，Chengdu 610031，China）

In the areas with sufficient rainfall and poor drainage，water in ballastless track has significant effect on the crack propagation．To analyze the distribution of water pressure and influential factors on water pressure in the ballastless track under high-frequency train load，based on the law of mass conservation and momentum theorem，the analytical expression of water pressure was deduced by using the control volume method．The finite element software ANSYS and CFX were used to analyze the influence of loading frequency，load amplitude，crack length and crack opening on water pressure．The theoretical results show that the maximum water pressure appears at the crack tip under loading，and decreases along the crack．The value of water pressure is proportional to load amplitude，square of loading frequency and inversely proportional to crack opening．At the frequency of 5 Hz and loading amplitude of 10 kN，the hydrodynamic pressure distributions resulted from experiment and theoretical computation are nearly identical，and the corresponding hydrodynamic pressure peaks are 0．177 and 0．161 kPa，respectively．

ballastless track；cracks；train；load；water pressure

U213．244

A

0258-2724（2016）01-0036-07 DO I：10．3969／j．issn．0258-2724．2016．01．006

2015-06-02

国家自然科学基金资助项目（51278431）；国家自然科学基金重点项目（U1434208）

曹世蒙（1988—），男，博士研究生，研究方向为轨道结构与轨道动力学，E-mail：531148108＠qq．com

杨荣山（1975—），男，副教授，博士，研究方向为轨道结构与轨道动力学，E-mail：yrs＠home．swjtu．edu．cn

曹世蒙，杨荣山，刘学毅，等．无砟轨道层恒裂纹内动水压力特性分析［J］．西南交通大学学报，2016，51（1）：36-42．