基于可靠度理论的铁路隧道洞门极限状态设计方法
蒙国往, 周佳媚, 高 波
(西南交通大学交通隧道工程教育部重点实验室,四川成都610031)
基于可靠度理论的铁路隧道洞门极限状态设计方法
蒙国往, 周佳媚, 高 波
(西南交通大学交通隧道工程教育部重点实验室,四川成都610031)
针对铁路隧道洞门结构稳定性极限状态功能函数具有非线性及其参数具有随机性的特点,提出了基于可靠度理论的铁路隧道洞门结构设计方法.通过分析铁路隧道洞门的极限状态,建立了其极限状态方程.基于可靠度理论,以时速140 km/h的单线电气化铁路隧道端墙式洞门可靠指标计算为例,根据采用同样方法对3种设计时速共16种形式、22种类别隧道洞门的可靠指标计算结果,确定各极限状态下的目标可靠指标,建立极限状态设计式,求解并优化抗力分项系数.研究结果表明:铁路隧道洞门主要有抗裂、抗压、倾覆、滑动和地基承载力不足5种极限状态;极限状态方程中基本随机变量的统计特征是铁路隧道洞门可靠度设计是否准确的关键,可靠指标的确定是洞门结构极限状态设计的核心;建立的极限状态设计方法可直接用于铁路隧道洞门结构设计.关键词:隧道工程;隧道洞门;极限状态;设计方法;可靠度
隧道洞门结构与周围岩土之间的相互作用关系复杂、岩土工程性质不确定性等[1],使得隧道洞门可靠性研究难度大.张清等提出了与地面结构相似的铁路隧道衬砌结构可靠度分析方法[2].景诗庭介绍了地下结构可靠度分析研究的进展[3].谭忠盛、高波等提出了基于有限单元法求解偏压隧道衬砌结构可靠度的方法,并开发了计算机程序[4].谭忠盛对隧道支护结构体系的可靠度进行了理论研究[5].周佳媚等对单线电气化铁路隧道极限状态设计式、分项系数等进行了研究[6].谭忠盛对隧道洞门进行了抗滑模型试验,提出了洞门抗滑可靠度的计算方法[7-8].李伦贵、高波对翼墙式洞门的可靠性进行了分析[9].宋玉香等对整个隧道结构体系可靠度进行了探讨[11].魏新欣等就公路隧道可靠度分析方法提出了概率极限状态设计的思路[12].
2005年,我国以规范形式将可靠度理论引入隧道结构设计,使隧道结构设计方法实现了从半概率法向近似概率法的过渡[10],但仅限于单线铁路隧道,双线、高速铁路隧道等仍然采用安全系数法.
目前国内对隧道洞门结构可靠度的研究很少,可靠度设计还达不到实用的程度.国外不少国家,如美国、加拿大、德国、日本等,已将结构可靠性理论应用到工程结构设计和分析中.国际标准化组织1998年颁布的ISO 2394《结构可靠性总原则》、欧洲标准委员会2002年颁布的EN 1990《结构设计基础》、结构安全度联合委员会2000年编制的《概率模式规范》等,集中体现了结构可靠度理论研究的最新成果.然而,目前关于极限状态设计方法的研究中,鲜有专门针对隧道洞门的,而是将其归到挡土墙大类,且可参考文献较少.
本文从铁路隧道洞门结构的工作状态出发,建立了其极限状态方程,通过对洞门结构可靠度的计算分析,给出了相应的极限状态设计表达式,求解分项系数并进行优化,探讨了基于可靠度理论的铁路隧道洞门的极限状态设计方法.
1 隧道洞门体系极限状态
1.1 洞门结构工作状态
在隧道洞门结构极限状态分析中,需要考虑与洞门体系极限状态和可靠度有关的各种参数,用随机变量Xi(i=1,2,…,n)表示.假定由随机变量Xi(i=1,2,…,n)组成的描述隧道洞门结构的功能函数Z=g(X1,X2,…,Xn),将功能函数中的基本随机变量组合成综合变量的形式,令产生作用或效应的各项之和为S,产生抗力的各项之和为R,则可将隧道洞门结构的工作状态表示为当Z>0时,表示结构处于可靠状态;当Z=0时,表示结构处于极限状态;当Z<0时,表示结构处于失效状态.

隧道洞门结构承载能力极限状态主要表现:墙身某部位因抗拉强度不足引起开裂;墙身某部位由于抗压强度不足引起压坏;洞门整体倾覆;洞门整体滑动和地基承载力不足.以上5种极限状态就是隧道洞门结构体系可能出现的5种失效模式.
1.2 洞门体系的极限状态方程
在隧道洞门结构分析中,将洞门端墙、翼墙和洞门挡土墙均视为挡土墙,采用分条方法近似计算[10].根据式(1),分别对以上5种失效模式建立极限状态方程.
洞门墙身抗裂承载能力极限状态方程:
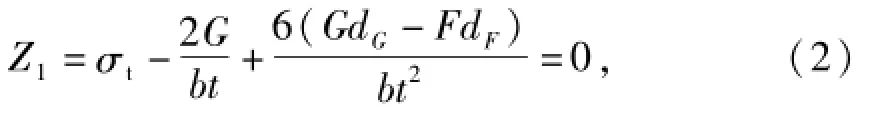
式中:σt为洞门墙身材料抗拉强度;b为洞门计算条带宽度;t为检算截面厚度;G为计算条带墙重力;F为计算条带土压力合力;dG和dF分别为计算条带墙重力和土压力合力至作用线的力臂.
洞门墙身抗压承载能力极限状态方程:
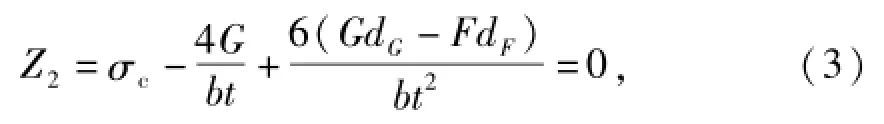
式中:σc为洞门墙身材料抗压强度.
倾覆稳定极限状态方程:

滑动稳定极限状态方程:

式中:μ为地基摩擦因数.
地基承载力极限状态方程:
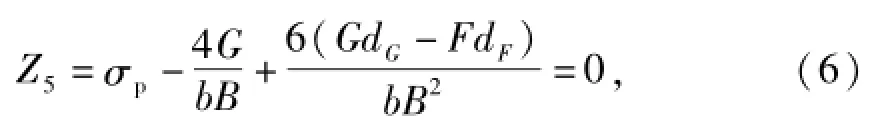
式中:σp为地基承载力极限强度;B为地基沿隧道纵向的宽度.
1.3 随机变量统计
隧道洞门极限状态方程中,共有6个基本随机变量和1个综合随机变量.其中,计算条带土压力合力F所需的地层重度、计算条带墙重力G所需的洞门材料重度、洞门墙身材料抗拉强度σt和抗压强度σc、地基摩擦因数μ和地基承载力极限强度σp为基本随机变量,计算土压力合力F所需的侧土压力系数为综合随机变量.随机变量的统计特征通过现场实测或室内模型试验统计分析确定.
2 隧道洞门可靠度
2.1 可靠度分析
以上5种失效模式中,只要其中任何1种或1种以上发生,都会导致洞门结构体系失效,因此,可以认为洞门结构体系是串联结构体系.5种失效模式承受的荷载基本相同,这些荷载主要是洞门墙背和侧面的主动土压力、墙趾前的被动土压力,以及结构本身的重力.隧道洞门结构设计中,洞门尺寸、边坡和仰坡角度一般为定值,洞门材料极限强度为随机变量.土压力计算时,土体的平均摩擦角、地基摩擦因数等为随机变量.获得所有随机变量的统计特征后,计算各种失效模式的失效概率.由于各种失效模式都采用相同的荷载进行计算,因此,它们之间有很强的相关性.
由于可靠指标计算方便、直接,迭代计算比较准确,因此,对于随机变量不服从正态分布或功能函数为非线性的结构可靠度分析计算,可采用可靠指标来评价结构体系的可靠度.由于失效概率更能直观表达结构体系的可靠度,如果基本随机变量服从正态分布或对数正态分布,可通过计算可靠指标求失效概率,进而对结构体系的可靠度进行评价.此时,可靠指标β与失效概率Pf的关系为[13]

式中:Φ(·)为标准正态分布函数.
根据式(1)对不同失效模式建立极限状态方程后,若极限状态方程中基本随机变量Xi(i=1,2,…,n)的概率密度函数fXi(x1,x2,…,xn)已知,则由这些随机变量表示的结构功能函数的失效概率
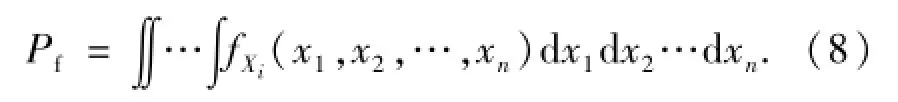
由式(8)可知,当基本随机变量较多、功能函数为非线性时,用数值积分法计算结构的失效概率将难以进行.另外,数值积分法的计算精度难以保证,基本随机变量的敏感度也无法反映.考虑以上不利因素,可采用JC法、分位值法、蒙特卡罗法等近似方法计算隧道洞门的可靠度.由于分位值法概念清晰、简便实用,且为目前我国铁路工程设计统一标准和铁路隧道设计规范中推荐采用的可靠指标计算方法,因此,采用分位值法对可靠指标进行计算.
如图1所示,以时速140 km/h的单线电气化铁路隧道端墙式洞门为例,采用分位值法对其可靠指标进行计算.

图1 洞门结构尺寸(单位:m)Fig.1 Size sketch of tunnel portal structure(unit:m)
洞门墙背土压力计算参照挡土墙的分条受力分析方法,计算公式为[10]
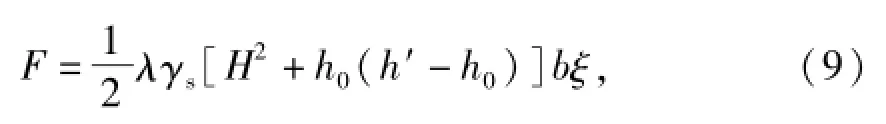
式中:λ为侧土压力系数;γs为地层重度;H、h0和h′分别为洞门墙背仰坡开挖高度、填埋高度和地层破裂面高度;ξ为土压力模式不定性系数.
由于土压力模式不定性系数缺乏大量统计数据作为取值依据,通过对时速140 km/h的单线电气化铁路6种隧道洞门、双线电气化铁路4种隧道洞门、时速200 km/h的单线电气化铁路2种隧道洞门和时速250 km/h的双线电气化铁路2种隧道洞门[14]的数值分析计算,确定土压力模式不定性系数取0.45.洞门墙背土压力计算中,H、h0和h′
取值见表1.

表1 土压力计算相关参数Tab.1 Parameters for calculating soil pressure
基本随机变量及其均值和标准差取值[14]见表2.
由式(2),可得洞门墙身抗裂函数
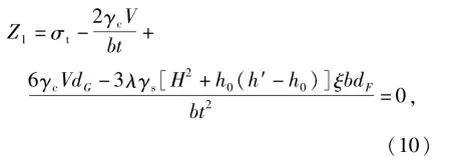
式中:γc为混凝土重度;V为计算条带体积.
由式(10)可知,抗裂函数中,洞门墙身材料抗拉强度σt、混凝土重度γc、地层重度γs和侧土压力系数λ共4个随机变量.
抗裂承载能力极限状态方程:
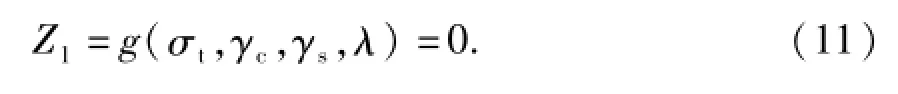
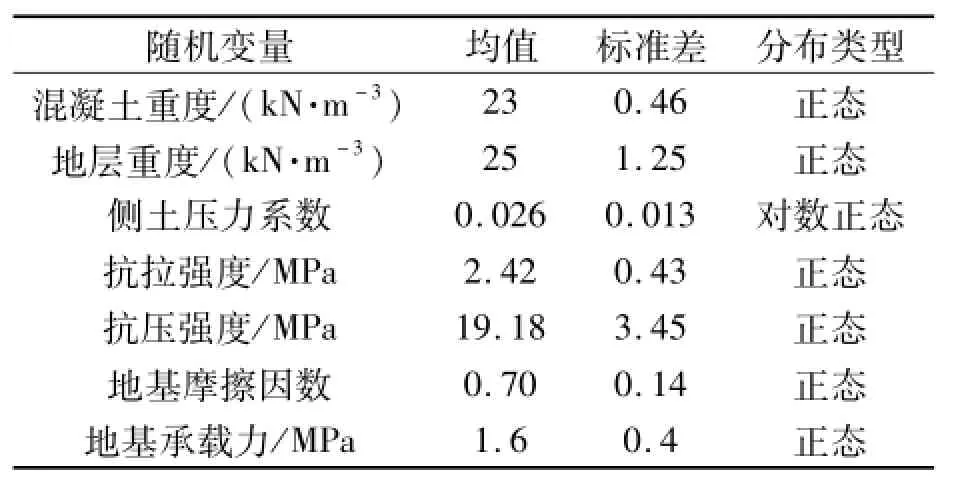
表2 随机变量的均值和标准差Tab.2 Mean and standard deviation of random variables
选取设计验算点初值时,各随机变量初值为其平均值,然后对函数g(σt,γc,γs,λ)在设计运算点处求各随机变量的偏导数及其相应的灵敏系数.假设各随机变量的初始可靠指标均为0,通过迭代的方法计算出新的验算点,当验算点变化量小于0.01,且式(10)等于或接近于0时,停止计算.由此计算出洞门抗裂承载能力极限状态下的可靠指标为4.03.
同理,可计算出洞门在另外4种极限状态下的可靠指标.由于基本随机变量均服从正态分布或对数正态分布,由式(7)可将可靠指标换算成失效概率.最终可得洞门在5种极限状态下的可靠指标和对应的失效概率,见表3.

表3 时速140 km/h的单线铁路隧道洞门的可靠度Tab.3 Reliability of tunnel portal for single track railway with a design speed of 140 km/h
2.2 目标可靠指标确定
目标可靠指标的确定通常有3种方法:事故类比法、经济优化法和经验校准法.实际设计中,用前2种方法确定目标可靠指标均有一定难度.经验校准法用可靠度方法分析按传统方法设计的可靠度水平,能充分体现工程建设长期积累的实践经验,继承原有设计规范的可靠度水准,并接受其总体上的合理性.因此,在铁路隧道洞门极限状态设计方法中,可采用经验校准法计算结构的目标可靠指标.经验校准法中,当根据目标可靠指标进行结构设计时,所设计结构的可靠指标应不低于目标可靠指标.因此,可按照目标可靠指标低于最小可靠指标的原则来确定隧道洞门在各极限状态下的目标可靠指标.由于已有较完善的铁路隧道洞门标准图,可基于经验校准法对铁路隧道洞门标准图进行检算,以确定目标可靠指标.
根据可靠指标确定的上述方法,分别对目前使用广泛的时速140 km/h的单线和双线电气化铁路隧道洞门中的端墙式洞门、柱式洞门、台阶式洞门、翼墙式洞门和耳墙式洞门,以及时速200 km/h的单线、时速250 km/h的双线电气化铁路隧道洞门的台阶式洞门、柱式洞门和耳墙式洞门标准图共16种形式、22种类别隧道洞门[14]的最不利部位计算5种极限状态下的可靠指标,按照目标可靠指标低于最小可靠指标的原则,确定铁路隧道洞门抗裂、抗压、倾覆、滑动和地基承载力极限状态下的目标可靠指标,结果见表4.
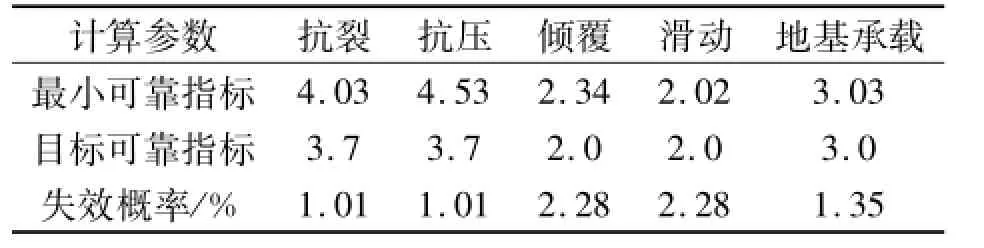
表4 隧道洞门最小可靠指标及目标可靠指标Tab.4 Minimum acceptable reliability indices and target reliability indices of tunnel portal
从表4可知,各极限状态下隧道洞门的目标可靠指标均达到2.0及以上,失效概率均在2.3%以内,即安全保证率均在97.7%以上.
3 隧道洞门极限状态设计式
作用在隧道洞门结构上的荷载主要有结构重力、土压力、水压力、施工荷载、温度应力、列车荷载、地震荷载等,其中土压力是洞门端墙承受的主要荷载,以上所有荷载作用的组合效应设计值

式中:γ0为结构重要性系数;S(·)为作用组合的效应函数;Gik和γGi分别为第i个作用标准值及其分项系数.
以材料性能分项系数表达的结构抗力设计值[15]

式中:R(·)为结构抗力的效应函数;fk为材料强度标准值;γm为材料性能分项系数;ak为材料几何尺寸标准值;Δa为几何参数的附加量.
将隧道洞门视作挡土墙,作用在洞门结构上的永久作用主要有洞门结构重力、侧土压力和水压力.隧道洞门设计中,目前一般不考虑水压力,则铁路隧道洞门极限状态设计表达通式为

式中:G1k和γG1分别为结构自重标准值及其分项系数;G2k和γG2分别为侧土压力标准值及其分项系数;fik和γfi分别为第i个抗力标准值及其分项系数.
根据式(14),结合式(2)~(6),可分别建立5种极限状态的设计表达式,其中包括土压力作用分项系数γG2、墙身材料抗拉强度分项系数γrt、墙身材料抗压强度分项系数γrc、地基摩擦力分项系数γrf和地基承载力分项系数γrp.
由式(2),有隧道洞门墙身抗裂承载能力极限状态设计表达式:
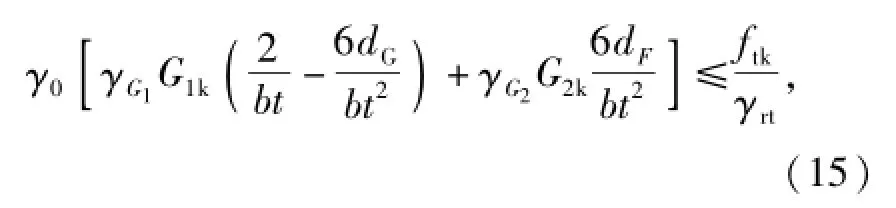
式中:ftk为洞门墙身材料抗拉强度标准值.
按照抗裂承载能力极限状态设计表达式建立的方法,可得隧道洞门墙身抗压承载能力极限状态设计表达式:
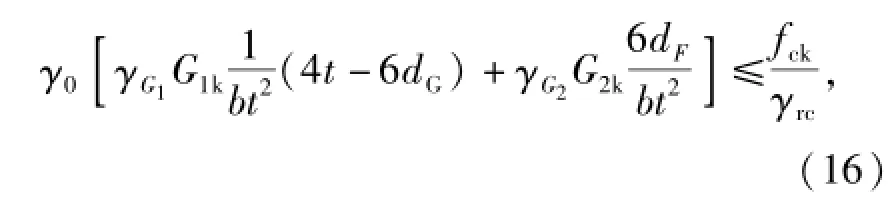
式中:fck为洞门墙身材料抗压强度标准值.
倾覆稳定极限状态设计表达式:

滑动稳定极限状态设计表达式:

式中:ffk为地基摩擦力标准值,ffk=μG1k.地基承载力极限状态设计表达式:
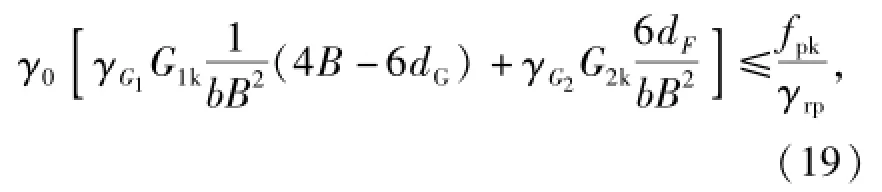
式中:fpk为地基承载力标准值.
4 分项系数计算
4.1 计算方法
各基本随机变量均呈正态或对数正态分布,可采用分位值法确定各分项系数[16].求出洞门在各极限状态下的目标可靠指标后,通过对极限状态方程中各随机变量进行“约化高斯变量”反变换,求得相应的理论设计值,则作用效应和材料抗力基本变量的分项系数分别为

式中:Xik为基本随机变量Xi的标准值;Xid为基本随机变量Xi的理论设计值.
结合表4中目标可靠指标计算结果,用分位值法分别对相应极限状态及其计算条件下的材料抗力基本变量分项系数进行计算,结果见表5.

表5 各极限状态设计式中的抗力分项系数Tab.5 Partial resistance coefficients in limit state design expressions
由表5可知,不同极限状态下的土压力作用分项系数不同,其中,墙身抗裂和抗压承载能力极限状态受土压力作用分项系数影响最大;同一极限状态下,除倾覆稳定极限状态只受土压力作用分项系数影响外,其余4种极限状态都受2种作用分项系数的影响,且均受土压力作用分项系数的影响,并且该影响最大.
4.2 分项系数优化
同一分项系数在不同极限状态设计表达式中的值应保持不变,因此,应对所有分项系数进行优化.由于各极限状态设计表达式中均含有土压力分项系数,优化原则是,在保证土压力分项系数在各极限状态设计表达式中相等的基础上,对其他分项系数进行优化.由于倾覆稳定极限状态设计表达式中仅含有土压力分项系数,因此,以倾覆稳定极限状态设计表达式中土压力分项系数2.3为标准,采用数值方法对其他分项系数进行优化.分项系数优化的数值计算过程:
(1)根据初始土压力分项系数及抗力分项系数,计算作用效应S和原始抗力R,从而得R-S;
(2)在土压力分项系数统一值取为2.3、抗力分项系数不变的情况下,得新的抗力与作用效应之差R′-S′;
(3)将R′-S′与R-S进行比较,调整抗力分项系数,使(R-S)-(R′-S′)≥0.
采用该数值计算方法对隧道洞门在各极限状态下的抗力分项系数进行优化,结果见表6.

表6 优化后的分项系数Tab.6 Optimized partial coefficients
为检验分项系数是否正确,将表6中优化后的分项系数代入上述5个设计表达式中进行检算.经检算,各形式洞门在5种极限状态下的抗力均大于作用效应,计算出的可靠指标均大于目标可靠指标,说明分项系数优化计算结果是正确的.
5 结 论
本文基于可靠度理论,针对铁路隧道洞门体系的极限状态设计方法进行了研究,获得以下主要结论:
(1)铁路隧道洞门极限状态设计方法研究的主要思路:建立极限状态方程→计算可靠指标并确定目标可靠指标→建立极限状态设计式→计算分项系数.
(2)建立了铁路隧道洞门抗裂、抗压、倾覆、滑动和地基承载力极限状态方程,方程中基本随机变量统计特征是洞门可靠度设计是否准确的关键,可靠指标的确定是洞门结构极限状态设计的核心问题.
(3)提出了铁路隧道洞门在各极限状态下的目标可靠指标建议值和相应极限状态设计式中的抗力分项系数建议值.对土压力作用的分析表明,影响铁路隧道洞门目标可靠指标和分项系数的关键是土压力计算方法和侧土压力系数取值.
(4)建立的极限状态设计方法可直接用于铁路隧道洞门形式的结构设计.
[1] 周佳媚.隧道洞门结构土压力的研究[D].成都:西南交通大学土木工程学院,2004.
[2] 张清,王东元,李建军.铁路隧道衬砌结构可靠度分析[J].岩石力学与工程学报,1994,13(3):209-218.ZHANG Qing,WANG Dongyuan,LI Jianjun.Reliability analysis of lining structures in Chinese railroad tunnels[J].Chinese Journal of Rock Mechanics and Engineering,1994,13(3):209-218.
[3] 景诗庭.地下结构可靠度分析研究之进展[J].石家庄铁道学院学报,1995,8(2):13-18.JING Shiting.The advance of reliability research of underground structure[J].Journal of Shijiazhuang Railway Institute,1995,8(2):13-18.
[4] 谭忠盛,高波,关宝树.偏压隧道衬砌结构可靠度分析[J].西南交通大学学报,1996,31(6):21-27.TAN Zhongsheng,GAO Bo,GUAN Baoshu.The structural reliability analysis of bias tunnel lining[J].Journal of Southwest Jiaotong University,1996,31(6):21-27.
[5] 谭忠盛.隧道支护结构体系可靠度的理论研究及其工程应用[D].成都:西南交通大学土木工程学院,1998.
[6] 周佳媚,严松宏,王英学.单线铁路隧道洞门结构分项系数的研究[J].西南交通大学学报,2001,36(5):505-508.ZHOU Jiamei,YAN Songhong,WANG Yingxue.Analysis of partial coefficients of single-track railway tunnel portal structures[J].Journal of Southwest Jiaotong University,2001,36(5):505-508.
[7] 谭忠盛.隧道洞门土压力的离心模型试验及计算模式不定性[J].西部探矿工程,2001(4):76,77.
[8] 谭忠盛.隧道洞门抗滑模型试验及可靠度分析[J].兰州铁道学院学报:自然科学版,2001,20(3):4-7.TAN Zhongsheng.A model experiment on the anti-sliding property of tunnel door and research on its reliability[J].Journal of Lanzhou Railway University:Natural Sciences,2001,20(3):4-7.
[9] 李伦贵,高波.翼墙式隧道洞门可靠性分析[J].西南交通大学学报,2002,37(5):496-499.LI Lungui,GAO Bo.Reliability analysis of wing wall tunnel portal[J].Journal of Southwest Jiaotong University,2002,37(5):496-499.
[10] 铁道第二勘察设计院.TB 10003—2005铁路隧道设计规范[S].北京:中国铁道出版社,2005.
[11] 宋玉香,景诗庭,朱永全.隧道结构系统可靠度研究[J].岩土力学,2008,29(3):780-784.SONG Yuxiang,JING Shiting,ZHU Yongquan.Research on reliability of tunnel structural system[J].Rock and Soil Mechanics,2008,29(3):780-784.
[12] 魏新欣,丁文其.公路隧道概率极限状态设计方法[J].公路交通科技,2011,28(10):75-79. WEI Xinxin,DING Wenqi.Probabilistic limit state design method of highway tunnel[J].Journal of Highway and Transportation Research and Development,2011,28(10):75-79.
[13] 赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑出版社,2000:17-19.
[14] 中铁二院工程集团有限责任公司,西南交通大学,石家庄铁道大学,等.铁路隧道结构极限状态设计方法研究[R].成都:中铁二院工程集团有限责任公司,2014.
[15] 中国建筑科学研究院.GB 50153—1992工程结构可靠度设计统一标准[S].北京:中国建筑工业出版社,2008.
[16] 铁道部科学研究院.GB 50216—1994铁路工程结构可靠度设计统一标准[S].北京:中国计划出版社,1994.
(中、英文编辑:付国彬)
Limit State Design Method of Railway Tunnel Portal Based on Reliability Theory
MENG Guowang, ZHOU Jiamei, GAO Bo
(Key Laboratory of Transportation Tunnel Engineering of Ministry of Education,Southwest Jiaotong University,Chengdu 610031,China)
From the characteristics that limit state functions for the stability of a railway tunnel portal structure are nonlinear and the parameters are random,a new design method for railway tunnel portal structures was put forward based on the reliability theory.Limit state equations for railway tunnel portal structures were founded by analyzing the limit states of railway tunnel portal.Based on the reliability theory,reliability indices of a single-track railway tunnel portal with a design speed of 140 km/h were calculated as an example,target reliability indices for different limit states were determined from the calculated reliability indices of railway tunnel portal under three design speeds,including 16 kinds of portal forms and 22 kinds of portal categories,and partial resistance coefficients were calculated and optimized based on establishing the design expressions for different limit states.The research results show that major limit states of railway tunnel portal are cracking,crushing,overturning stability,sliding stability and insufficient foundation bearing capacity;the statistical characteristics of basic random variables in the limit state equations are the key whether reliability design of railway tunnel portal is accurate or not,and the determination of the reliability indices is the core issue in the limit state design of railway tunnel portal.The established method can be directly used to the limit statedesign of railway tunnel portal.
tunnel engineering;tunnel portal;limit state;design method;reliability
U451
A
0258-2724(2016)01-0030-07
10.3969/j.issn.0258-2724.2016.01.005
2015-01-25
中国铁路总公司科技研究开发计划资助项目(2012G014-D)
蒙国往(1987—),男,博士研究生,研究方向为隧道及地下结构,电话:15982305298,E-mail:menggwang@163.com
周佳媚(1973—),女,教授,博士,研究方向为隧道及地下结构,电话:13018264335,E-mail:tmzjm@home.swjtu.edu.cn
蒙国往,周佳媚,高波.基于可靠度理论的铁路隧道洞门极限状态设计方法[J].西南交通大学学报,2016,51(1):30-35,49.

