落石冲击力评定的离散元颗粒流数值模拟
王玉锁, 李俊杰, 李正辉, 冯高飞, 吴 浩, 何俊男
(1.西南交通大学土木工程学院,四川成都610031;2.西南交通大学地球科学与环境工程学院,四川成都610031)
落石冲击力评定的离散元颗粒流数值模拟
王玉锁1, 李俊杰2, 李正辉2, 冯高飞1, 吴 浩1, 何俊男2
(1.西南交通大学土木工程学院,四川成都610031;2.西南交通大学地球科学与环境工程学院,四川成都610031)
为使落石冲击力评定更合理、有效,以离散元模型(DEM)为理论基础,利用颗粒流(PFC)单元法研究垂直下落条件下落石对结构的冲击力,分析了落石高度、重力及回填土厚度对冲击力的影响规律.将PFC数值模拟结果与其他几种落石冲击力计算方法所得结果进行比较,结果表明:落石冲击力与落石高度及重力均呈明显的线性关系,落石冲击力随落石高度线性变化幅度与落石重力有关,而落石冲击力随落石重力线性变化幅度与回填土厚度有关;回填土厚度为0.6m时的冲击力比无回填土时减小50%~60%,回填土厚度大于2.0m时,缓冲幅度趋于稳定,说明回填土厚度有一个合理范围,超出时,结构总荷载会增大;离散元颗粒流数值模拟方法通过阻尼设置来模拟空气在落石下落过程中产生的作用,使得在评定大体积落石从较高高度下落时产生的冲击力更加合理.
落石冲击力;回填土;离散元模型(DEM);颗粒流(PFC)
落石灾害在我国山区铁路、公路修建及运营过程中经常出现,例如宝成线K307+100-K308+720段20年间发生46起较大落石灾害,损坏轨道、列车和输电网,引发停车事故.5.12地震时,边坡崩塌和落石引起宝成线109隧道洞口结构严重破坏.成昆铁路北段,1971至1992年间发生落石灾害214处共218次.据不完全统计,全国铁路每年落石灾害数千次.因此,落石灾害已成为山区交通运输安全的重要影响因素,落石对铁路、公路工程结构的冲击效应日益引起各方关注并展开深入研究[1-3].
在落石冲击力评估或计算方面,西南交通大学杨其新、关宝树[4]在较早时期利用铁球垂直下落冲击结构顶板的方法,得出了垂直下落条件下落石冲击力的计算经验公式.我国路基规范、隧道手册等根据冲量定理提出了相应的落石冲击力的计算方法[5-6].国外包括日本道路协会(Japan Road Association)方法[7]、Vincent Labiouse博士等提出的计算方法[8].
由于试验条件及计算参数选取等因素的限制,以上这些落石冲击力评定方法在同样条件下所得到的结果差异较大,说明各种方法都有一定的适用性和局限性[9].防落石冲击措施尤其是被动防护结构如隧道棚洞、拱形明洞等的设计目前仍主要采用经验方法,缺乏设计理论指导.因此有必要深入研究落石冲击力的确定方法.
近年来,采用离散单元模型(discrete element modeling,DEM)模拟落石灾害的研究成为一种趋势[10-13].本文采用三维离散元颗粒流(particle flow code in 3 dimensions,PFC3D)方法,研究了在垂直下落条件下,落石高度、重力及回填土厚度等因素对落石冲击力的影响规律,对合理回填土厚度进行了探讨,介绍了离散元颗粒流方法的基本原理及模型设置,并与其他落石冲击力计算方法得到的结果进行了分析比较.
1 离散元颗粒流理论基础及模型设置
1.1 PFC3D简介及离散单元模型基本理论
基于离散单元方法,PFC3D软件由“Itasca公司”发行.模型是由可独立运行的球体颗粒单元及墙单元组成,球体单元之间以及球体与墙体单元之间的相互作用是以牛顿第二运动定律为理论基础[12,14-15].本次所用到的本构关系包括接触刚度、粘结、滑动等可参见文献[16].
1.2 落石冲击模型及计算工况
初速度为零、垂直下落条件下,研究不同高度、重力的落石,对具有不同厚度的回填土的结构(顶面)引起的冲击力.其中,落石采用单个刚性球体单元(ball),根据落石物理性质设定其容重或天然密度,通过改变球体颗粒的大小(半径)获得不同重力的落石.本次研究没有考虑落石下落及冲击过程中的碎裂.利用多个球体单元(ball)的集合模拟回填土,通过接触粘结模型,模拟回填土与落石的相互作用,以及回填土受力的分布及传递.回填土底部为半平面无限刚性体,用墙单元(wall)模拟.
应用颗粒流PFC3D建模软件模拟落石在垂直下落条件下,对不同回填土厚度的结构冲击过程.落石下落的过程中,考虑重力、黏滞阻力和碰撞力,其中阻尼采用黏滞阻尼,法向和切向黏滞阻尼系数都取0.2[17].
回填土范围为10 m×10 m(长×宽),用球体单元模拟,通过改变球体单元数量来获得不同回填土厚度,在四周用墙单元将回填土约束,底部wall用来模拟结构.计算模型见图1.
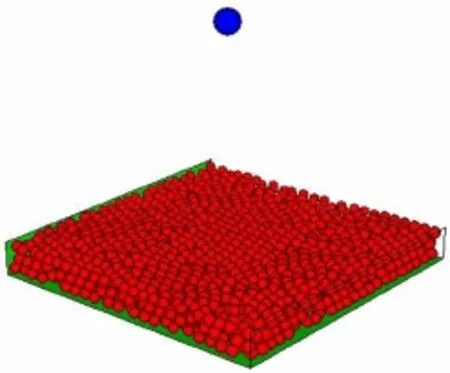
图1 落石冲击计算模型Fig.1 PFC3D rockfall model of impact progress on base structure with backfill soil
落石高度H、重力W及回填土厚度h取值见表1.

表1 落石冲击数值模拟工况Tab.1 Working conditions of rockfall impact numerical simulation
为全面评价各因素对落石冲击力的影响,本次采用全面组合,故共有5×6×7=210种计算组合情况.
1.3 材料单元参数设置
1.3.1 PFC3D模型材料细观参数
对所选用的各PFC3D单元(ball,wall)需要设置对应的细观参数.根据颗粒流理论及相关资料,对落石冲击模型的细观参数设置如表2所示.
1.3.2 回填土颗粒模型宏观力学参数的校准
由于PFC模型中,颗粒单元间的细观力学参数并不是所模拟材料的实际宏观力学参数,故需要对所采用的单元颗粒的细观力学参数进行校准,使模型材料的微观力学与实际工程材料的力学参数一致.

表2 模型材料单元细观参数Tab.2 Micro-properties of the model
采用PFC3D模拟回填土的三轴试验[18].试验样本采取与回填土模型相同的细观特性参数及排列方式,单元半径为0.200 3 m.试验尺寸高4 m,直径2 m,围压分别取25、50、100、150和200 kPa.三轴试验试样见图2.
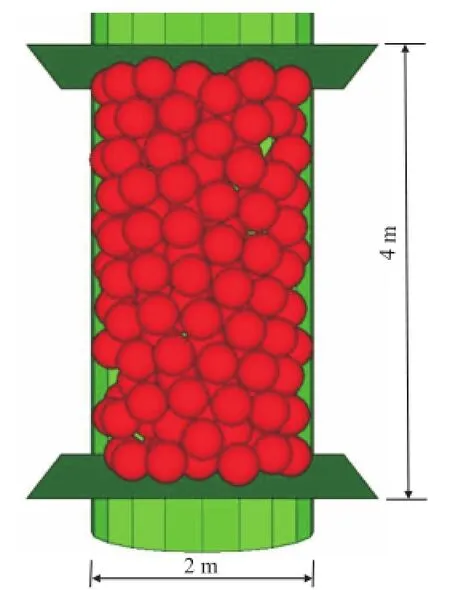
图2 PFC3D三轴数值模拟试验Fig.2 Numerical simulation of triaxial test
由三轴数值模型试验可得到相应的应力-应变、体积应变-轴向应变曲线,根据弹性理论,推导出弹性模量与压缩模量间的换算关系,用应力为100~200 kPa段割线计算压缩模量E12,用压缩模量Es来表示土的压缩性[19-20],由此得出回填土模型材料的压缩模量Es及泊松比ν.同时,根据不同围压下的试验结果,可绘出回填土模型材料的莫尔圆,进而得出回填土模型材料抗剪强度的指标黏聚力c及内摩擦角φ.
根据土的弹性模量Eo与压缩模量之间的关系如式(1),可得到弹性模量Eo.

由此,得出回填土模型材料的宏观力学参数如表3.

表3 三轴试验数值模拟宏观参数结果Tab.3 Micro-properties results from numerical simulation of triaxial test
将该结果与工程地质手册(2006版)[21]中土的平均物理力学指标对比,基本接近有关回填土的宏观物理力学指标,故所设计的回填土颗粒模型及细观参数能够反映实际回填土的物理力学性能.
2 数值模拟结果及分析
2.1 落石冲击力评定
由PFC3D计算得到回填土底部结构所受到的接触力记录情况如图3所示.
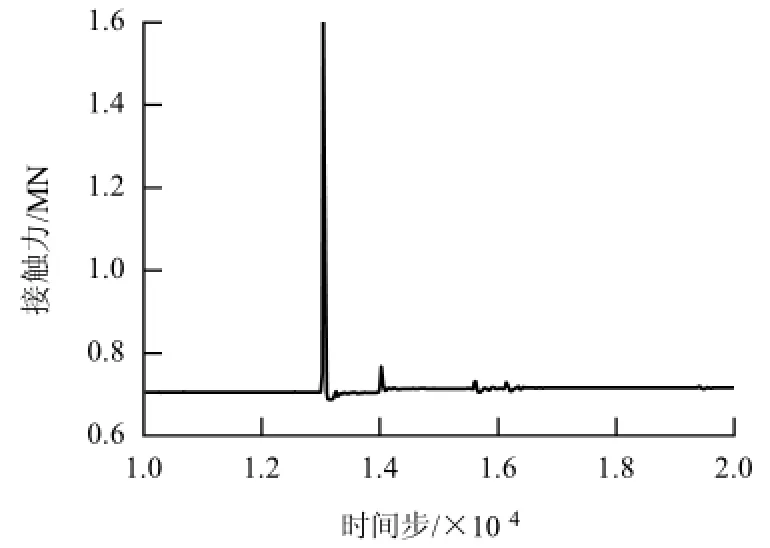
图3 回填土底部结构接触力Fig.3 Impact force of wall
根据所得到的回填土底部结构接触力(图3)随时间变化的记录曲线,通过读取接触力突变处的峰值,该峰值减去由回填土自重引起的平均接触力(图3中呈水平分布曲线部分为回填土自重引起的接触力),即可得到最大落石冲击力,也就是本文中所称的落石冲击力.

图4 落石冲击力与落石高度的关系Fig.4 Relationship between impact force and height of rockfall
2.2 落石冲击力影响因素及规律
根据计算结果,落石冲击力与落石高度、重力及回填土厚度的关系如图4~图6所示(只列出部分结果).
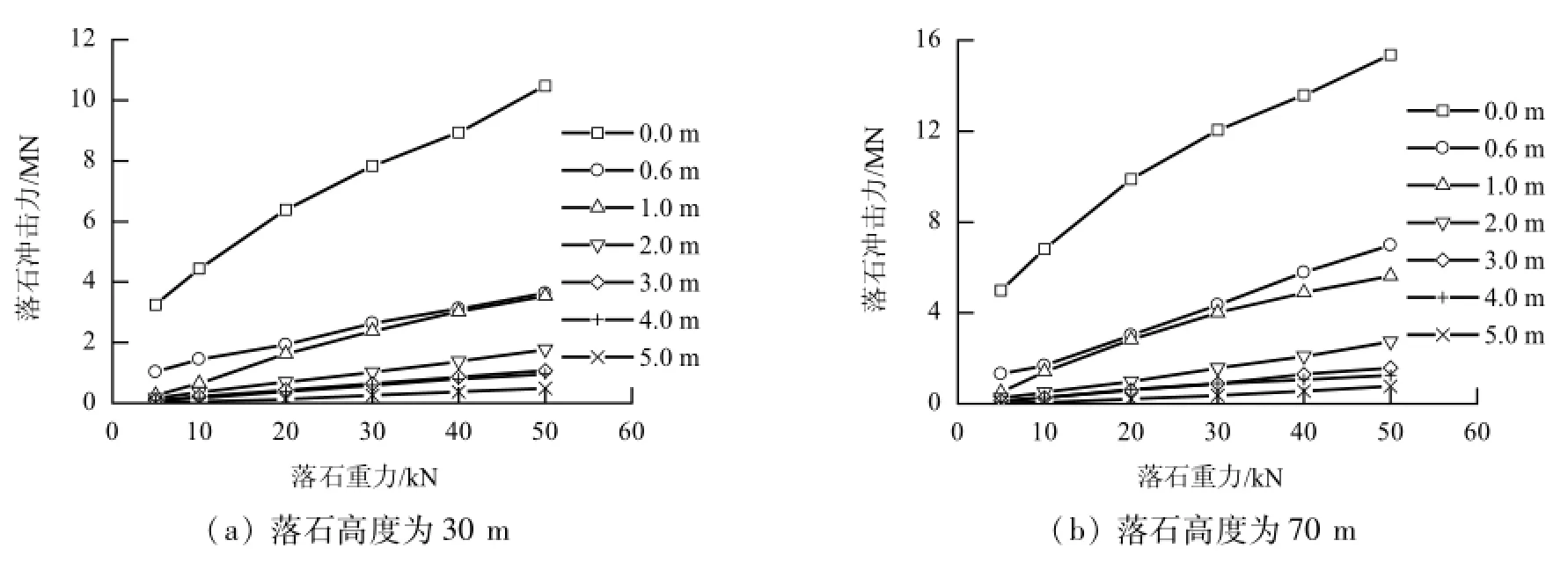
图5 落石冲击力与落石重力的关系Fig.5 Relationship between impact force and gravity of rockfall
由图4~图6可知,在垂直下落条件下:
(1)落石冲击力随落石高度增大而增大,且线性关系较为明显(图4),当回填土厚度一定时,冲击力增大的幅度或趋势线的斜率与落石重力有关,重力越大,冲击力变化幅度也越大;从图4可看出,各系列的曲线的垂直分离程度明显,说明落石重力是影响冲击力的重要因素.
(2)落石冲击力随落石重力增大而增大,且线性关系较为明显,而无回填土时,结构受到的落石冲击力明显大于有回填土情况(图5),落石高度一定时,冲击力增大的幅度或趋势线的斜率与回填土厚度有关,厚度越小,冲击力变化幅度越大;从图4曲线的上下分离看,无回填土趋势线明显高于有回填土的各趋势线,说明回填土缓冲作用明显,即使厚度为0.6 m也可缓冲至少一倍的冲击力;同时从图5可以看出,回填土厚度越大,冲击力随落石重力的变化趋势越不明显.
(3)从图6可明显看出回填土对结构所受落石冲击力的缓冲作用,同时从图5可明显看出,在本次计算范围内(回填土厚度0.6~5 m),回填土可缓冲至少一半的落石冲击力.但当回填土达到一定厚度时,落石冲击力变化会趋于稳定,说明回填土厚度有一个合理值或范围.在本次计算条件下,即落石垂直下落、最大高度为90 m及落石最大重力为50 kN(体积大约为2.5 m3)条件下,回填土厚度2~3 m为合理厚度,如再增大,则会使结构所受的总荷载效应(冲击力+回填土自重)增大.
2.3 数值模拟结果与已有方法计算结果对比
国内外现有的5种冲击力计算方法分别为铁路工程设计技术手册隧道版[6](后面简称“隧道手册方法”)、西南交通大学杨其新、关宝树方法[4](后面简称“交大方法”)、公路路基设计规范[5](后简称“路基规范方法”)、日本道路协会(Japan Road Association)方法[7](后简称“日本方法”)和Vincent Labiouse博士等人提出的计算公式[8](考虑到该公式主要建立在瑞士学者的研究基础上,故后面简称“瑞士方法”).前述方法所用的公式见所引文献.

图6 落石冲击力与回填土厚度的关系Fig.6 Relationship between impact force of rockfall and thickness of backfill soil
日本方法中的拉梅常数λ建议取1 000 kN/m2,实际工程中此值变化范围较大[7],故本次研究对于拉梅系数的取值分别用建议值和弹性理论换算值[22].
而瑞士方法中,ME是通过标准荷载板试验得到的基床反力系数,在原文中作者按砂砾垫层取ME=3 200 kN/m2[8],本次研究中,ME分别按原文的取值和弹性换算[23]取值ME=96 023.8 kN/m2.
现选取数值模拟工况(表1)中落石重力为5、 10、20、30、40和50 kN,回填土厚度h为1 m,落石下落高度H为10、30、50、70和90 m共30种工况,按以上5种计算方法分别计算落石冲击力,并与颗粒流数值模拟结果进行对比.5种方法所需基本计算参数见表4,计算中涉及到的其他参数均是通过所给基本参数计算得到.表4及以上各方法中涉及到的回填土及落石的物理力学参数均按数值模拟方法中的参数选取.

表4 计算参数Tab.4 Caculate parameters
另外,为便于对比分析,也比较了无回填土即h=0时的数值模拟结果.
由此,当给定落石重力时,由不同计算方法及参数,共得到9个系列的落石冲击力随高度变化的趋势线,分别为:
①PFC数值模拟1 m厚回填土;
②PFC数值模拟无回填土;
③隧道手册方法;
④路基规范方法;
⑤交大方法;
⑥日本方法按建议值(λ=1 000 kN/m2);
⑦日本方法按计算值(λ=21 994.7 kN/m2);
⑧瑞士方法,ME=3 200 kN/m2;
⑨瑞士方法,ME=96 023.8 kN/m2.
落石冲击力比较情况见图7,为便于比较分析,图中的趋势线对应的系列名称总体上从上到下按落石冲击力由大到小排列,例如图7(a)中,PFC数值模拟无回填土(h=0)时,对应落石冲击力最大,瑞士方法(ME=96 023 kN/m2)次之,以此类推,而PFC数值模拟结果(回填土厚h=1m)结果最小.

图7 不同方法冲击力计算结果Fig.7 Results of impact force using different methods
从图7可以看出,9个系列的趋势线具有如下特征:
(1)PFC数值模拟无回填土、日本方法及瑞士方法涉及的λ和ME分别按弹性理论公式求得.3者结果(对应的趋势线系列名称分别为“PFC h=0”、“日本(λ取值为21 994 kN/m2)”及“瑞士(ME取值为96 023 kN/m2)”较为接近,所得的落石冲击力最大;当落石重力越大且落石高度也增大时,PFC数值模拟无回填土即“PFC h=0”落石冲击力与其他两种方法差距越来越显著.
(2)当落石重力较小时(如5 kN)时,隧道手册方法得到的落石冲击力变化趋势与路基方法、日本及瑞士方法(λ和ME分别为1 000和3 200 kN/m2)三者结果接近,当落石重力及高度增大时,结果越来越大,也越接近PFC无回填土的结果.
(3)路基方法、日本及瑞士方法(λ和ME分别为1 000和3 200 kN/m2)三者结果接近,而路基方法偏大.
(4)当落石重力较小(如5,10 kN)时,PFC数值模拟有回填土即“PFC h=1 m”结果与交大方法接近,而当落石重力较大时,则与路基方法、日本及瑞士方法(λ和ME分别按1 000和3 200 kN/m2)三者结果接近,稍大于交大方法的结果.
通过以上各结果的相互验证、比较,可有如下分析或推论:
(1)日本方法与瑞士方法中,拉梅常数λ及基床反力系数ME的取值对结果影响较大,原方法中建议取λ=1 000 kN/m2和ME=3 200 kN/m2,所得结果较为合理,与我国路基规范方法所得结果较为接近;而这两个参数如果按弹性理论公式换算后,所得冲击力结果偏大,甚至比由PFC数值模拟无回填土结果还大,说明回填土缓冲效果不能按弹性理论求解,这也同时从侧面反映出PFC数值模拟方法的合理性.
(2)由于瑞士、日本方法中,并未涉及落石下落过程中空气等的阻力影响,而PFC数值模拟中则通过阻尼系数的设置(取推荐值0.2)来反映空气阻力.当落石高度不高或重力(体积)不大时,影响不明显;但当落石高度和体积增大,空气的阻力影响程度会加大,这可从图7中各图的最上面3条趋势线(“PFC h=0”、“日本(λ=21 994 kN/m2)”及“瑞士(ME=96 023 kN/m2)”3个系列)随落石高度增大而上下分离越来越明显看出.
(3)PFC数值模拟1 m厚回填土(“PFC h=1 m”)结果,当落石重力较小(10 kN以下)或落石高度较小(30 m以下)时,与交大方法结果接近,而当落石重力较大或高度较大时,则与路基方法、日本及瑞士方法(λ和ME分别按1 000和3 200 kN/m2)三者结果接近,比交大方法偏大而小于隧道手册方法.
通过以上综合比较分析,可认为颗粒流落石冲击数值模拟方法能更加全面的考虑各种落石冲击影响因素,所得到的结果也较为合理.
3 结 论
基于离散元模型理论,通过颗粒流PFC3D模拟分析,对垂直下落条件下落石引起的地基或结构的冲击力进行了研究,分析了落石高度、重力及回填土厚度对冲击力的影响规律,得出如下结论:
(1)落石冲击力随落石重力及高度增大而增大,且线性关系明显,在其他条件一定时,可认为冲击力分别与落石重力及高度成正比关系;当落石高度一定时,冲击力随落石重力的变化幅度与回填土厚度有关,厚度越小,变化幅度越大;当回填土厚度一定时,冲击力随落石高度的变化幅度与落石重力有关,重力越大,变化幅度越大.
(2)回填土厚度对落石冲击力缓冲作用明显,当回填土厚度为0.6m时,即可缓冲一半以上的落石冲击力;当回填土厚度为2~3 m时,落石冲击力变化已趋于稳定,当进一步增大厚度,缓冲作用已不明显,反而会使结构所受的总荷载(冲击力+回填土自重)增大.因此,从防落石角度出发,结构合理回填土厚度为2~3 m.
(3)由于试验条件及参数选取问题,现有的国内外几种落石冲击力评定方法都有一定的局限性和适用性,而PFC数值模拟方法能方便的考虑各种影响因素.通过与国内外不同落石冲击力方法的对比,用离散元颗粒流数值模拟方法得到的落石冲击力较为合理.
[1] 胡厚田.崩塌与落石[M].北京:中国铁道出版社,1998:71.
[2] 王玉锁,杨国柱.隧道洞口段危岩落石风险评估[J].现代隧道技术,2010,47(6):33-39.WANG Yusuo,YANG Guozhu.Rockfall risk assessment for a tunnel portal section[J].Modern Tunnelling Technology,2010,47(6):33-39.
[3] 王玉锁.高速铁路隧道洞口段危岩落石运动轨迹及冲击特性研究[J].前言动态,2011(2):16-21.
[4] 杨其新,关宝树.落石冲击力计算方法的试验研究[J].铁道学报,1996,18(1):101-106.YANG Qixin,GUAN Baoshu.Test and research on calculating method of falling stone impulsive force[J].Journal of the China Railway Society,1996,18(1):101-106.
[5] 交通部第二公路勘察设计研究院.JTJ013—95,公路路基设计规范[S].北京:人民交通出版社,1995.
[6] 铁道第二勘测设计院.铁路工程设计技术手册.隧道[M].2版.北京:中国铁道出版社,1995:148-150.
[7] KAWAHARA S,MURO T.Effects of dry density and thickness of sandy soil on impact response due to rockfall[J].Journal of Terramechanics,2006,43(3):329-340.
[8] LABIOUSE V,DESCOEUDRES F,MONTANI S.Experimental study of rock sheds impacted by rock blocks[J].Sruct.Eng.Int.,1996,3(1):171-175.
[9] 唐建辉.落石冲击对隧道明洞结构的影响研究[D].成都:西南交通大学,2013.
[10] ASHAYER P.Application of rigid body impact mechanics and discrete element modeling to rockfall simulation[D].Toronto:Department of Civil Engineering University of Toronto,2007.
[11] THOENIK,GIACOMINIA,LAMBERT C,et al.A 3D discrete element modelling approach for rockfall analysis with drapery systems[J].International Journal of Rock Mechanics&Mining Sciences,2014,68:107-119.
[12] CUNDALL P A,HART R D.Numerical modeling of discontinua[J].Engineering Computations,1992,9(2):101-113.
[13] CUNDALL P A,STRACK O D L.A discrete numerical model for granular assemblies[J].Geotechnique,1979,29(1):47-65.
[14] SHIUW J,DONZÉF V.Numerical study of rockfalls on covered galleries by the discrete elements method[c]∥Annual Report 2004.Grenoble cedex 9 France:[s n],2005:67-82.
[15] DONZE F V,RICHEFEU V,MAGNIER S A.Advances in discrete element method applied in soil,rock,concrete mechanics[J].Electronic Journal of Geotechnical Engineering,2009,8:1-44.
[16] 郑智能,张永兴,董强,等.边坡落石灾害的颗粒流模拟方法[J].中国地质灾害与防治学报,2008,19(3):46-49.ZENG Zhineng,ZHANG Yongxing,DONG Qiang,et al.Visual simulation of rock-fall of slope based on particle flow theory[J].Journal of Geological Hazard and Control,2008,19(3):46-49.
[17] ItascaConsulting Group.Inc.PFC3D(particle flow code in three dimensions)version 4.0 manual[M].Minneapolis:Itasca Consulting Group Inc.,2008:1-5
[18] 李广信.高等土力学[M].北京:清华大学出版社,2004:114-130.
[19] 王玉锁,王明年,童建军,等.砂类土体隧道围岩压缩模量的试验研究[J].岩土力学,2008,29(6):1607-1617.WANG Yusuo,WANG Mingnian,TONG Jianjun,et al.Test research on compression modulus of sandy soil tunnel surrounding rock[J].Rock and Soil Mechanics,2008,29(6):1607-1617.
[20] 王玉锁.砂质土隧道围岩力学参数及分级方法研究[D].成都:西南交通大学,2008.
[21] 工程地质手册[M].4版.中国建筑工业出版社,2006:192.
[22] 王光钦.弹性力学[M].北京:中国铁道出版社,2008:131.
[23] 黄斌,罗菊,何晓民等.基床系数的试验方法及合理取值[J].四川大学学报:工程科学版,2007,39(增刊):61-65.HUANG Bin,LUO Ju,HE Xiaomin,et al.Research on test method and reasonably valuing of coefficient of subgrade reaction[J].Journal of Sichuan University:Engineering Science Edition,2007,39(Sup.):61-65.
(中、英文编辑:徐 萍)
Assessment of Rock fall Impact Force by Particle Flow Code Numerical Simulation Based on Discrete Element Model
WANG Yusuo1, LI Junjie2, LI Zhenghui2, FENG Gaofei1, WU Hao1, HE Junnan2
(1.School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,China;2.Faculty of Geosciences and Environmental Engineering,Southwest Jiaotong University,Chengdu 610031,China)
To make a reasonable and effective assessment of rockfall impact force,a study on the impact force of falling down rockfall to a structure was carried out by using the method of PFC(particle flow code)based on the theory of DEM(discrete element model).The effects of rockfall height and gravity,and backfill soil thickness on the impact force were analyzed.The results of PFC numerical simulation were compared with those reached by other kinds of calculation methods.The results show that there is an obvious linear relationship between the impact force and the rockfall height or gravity.The linear variation range of the impact force with the changing of the rockfall height relates to the rockfall gravity,while the linear variation range of the impact force with the changing of the rockfall gravity relates to the backfill soil thickness.The impact force reduces by 50%-60%when the backfill soil thickness is 0.6 meter compared with no backfill soil.it tends to be stable when the backfill soil thickness is more than 2meters,showing that there is a reasonable range of the backfill soil thickness.The total load of structure will increase if the backfill soil thickness exceeds the range.The method of PFC numerical simulation can simulate the effect of air acting on rockfall by setting damping coefficient,which makes the assessment of bigger size rockfall impact force more reasonable.
impact force of rockfall;backfill soil;discrete element model;particle flow code
P642.21
A
0258-2724(2016)01-0022-08
10.3969/j.issn.0258-2724.2016.01.004
2015-11-16
四川省科技计划资助项目(2013GZ0047)
王玉锁(1974—),男,副教授,博士,研究方向为地下工程结构及工程材料,E-mail:wangysuo@home.swjtu.edu.cn
王玉锁,李俊杰,李正辉,等.落石冲击力评定的离散元颗粒流数值模拟[J].西南交通大学学报,2016,51(1):022-029.

