从一道习题谈起
安徽省蚌埠市第五中学
支 军 (邮编:233000)
从一道习题谈起
安徽省蚌埠市第五中学
支 军 (邮编:233000)
先看一道习题:
若直线l与曲线C满足下列两个条件:
(i)直线l在点P(x0,y0)处与曲线C相切;(ii)曲线C在P附近位于直线l的两侧,则称直线l在点P处“切过”曲线C.
下列命题正确的是______(写出所有正确命题的编号)
以下是笔者对本题的研究和思考:
本题实质是中心对称函数的一个性质,即:如果函数y=f(x)关于点P(x0,y0)对称且在点P(x0,y0)处连续且可导,则函数y=f(x)的图象在点P(x0,y0)处的切线一定“切过”y=f(x)的图象.由此性质易知本题选①③④.
但进一步引起笔者思考的是如何快速找到一些中心对称函数的对称中心.为此笔者进行了如下探究:
首先,我们来探究,原函数对称时,导函数的对称性如何?
若函数f(x)关于x=a对称且可导,则f(x)=f(2a-x).
根据复合函数导数的性质易得:f′(x)=-f′(2a-x),所以导函数f′(x)关于点(a,0)对称.
同理可得:若函数f(x)关于点(h,k)对称且可导,则导函数f′(x)关于直线x=h对称.
因此,我们得到如下结论:
定理1 若函数f(x)关于x=a对称且可导,则导函数f′(x)关于点(a,0)对称.若函数f(x)关于点(h,k)对称且可导,则导函数f′(x)关于直线x=h对称.
推论 若函数f(x)为偶函数且可导,则导函数f′(x)为奇函数;若函数f(x)为奇函数且可导,则导函数f′(x)为偶函数.
下面我们来探究导函数对称时,原函数的对称性如何.
若导函数f′(x)关于直线x=a对称,则f′(x)=f′(2a-x).所以
∫f′(x)dx=∫f′(2a-x)dx,
故f(x)+c=-f(2a-x)+d.
而当f′(x)关于点(h,k)对称时,有
f′(x)=2k-f′(2h-x),
故∫f′(x)dx=∫[2k-f′(2h-x)]dx,
所以f(x)+c=2kx+f(2h-x)+d.
可见,此时原函数f(x)不一定关于直线对称.例如,三次函数都是中心对称的,而四次函数中f(x)=x4是关于x=0对称的;f(x)=x4-3x3+2x却不是轴对称的(如图).

因此,我们得到如下结论:
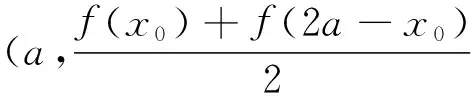
利用上述结论我们可以得到对三次函数f(x)=ax3+bx2+cx+d的对称中心的新求法.
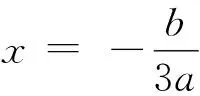
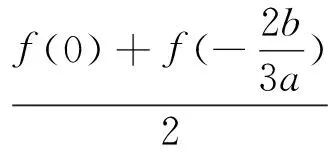
2016-09-21)

