旧题赋新意 老树开新花
安徽省合肥市第四十八中学
史承灼 魏大付 (邮编:230061)
复习考试
旧题赋新意 老树开新花
安徽省合肥市第四十八中学
史承灼 魏大付 (邮编:230061)
2016年安徽中考数学压轴的第23题似曾相识,又推陈出新, 立意新颖,引起广泛关注.下面试对该题进行探源、探析.
1 原题呈现
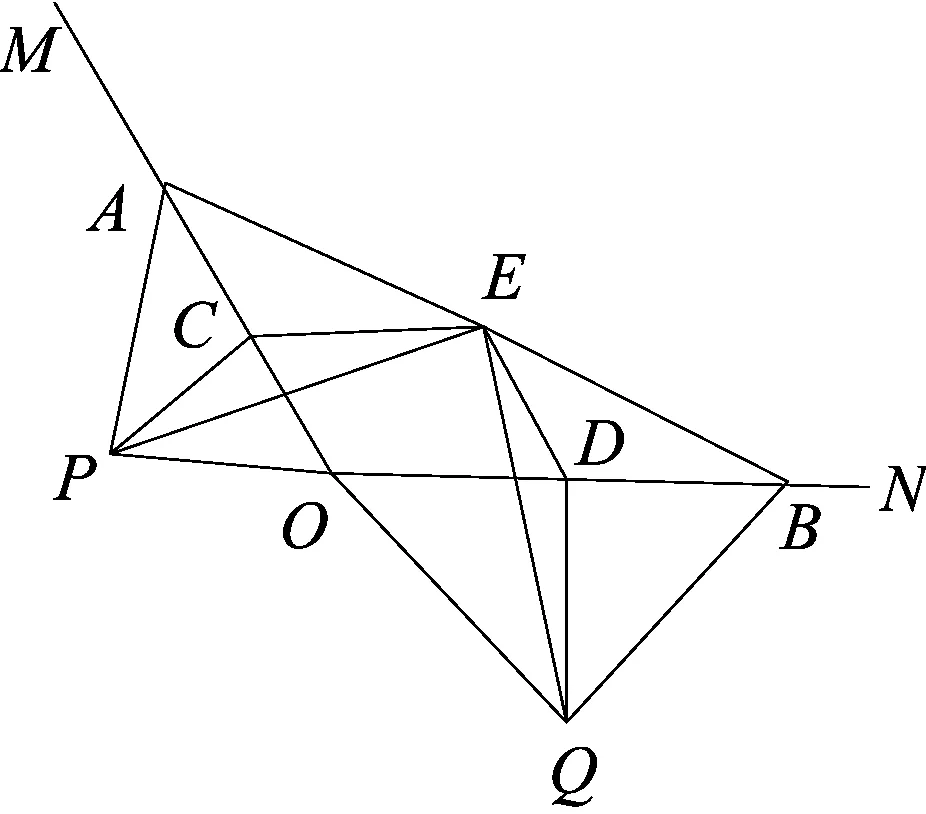
图1
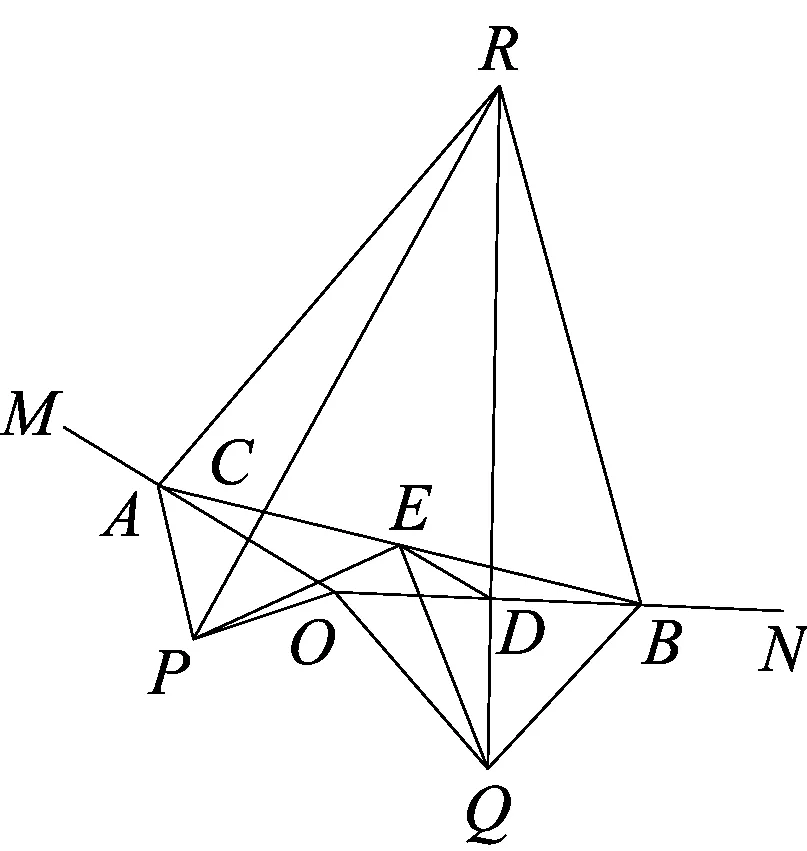
图2

图3
如图1,A、B分别在射线OM、ON上,且∠MON为钝角.现以线段OA、OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP、△OBQ,点C、D、E分别是OA、OB、AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC、QD交于点R.
①如图2,若∠MON=150°,求证:△ABR为等边三角形;
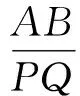
2 试题探源
此题源于两道姊妹题.
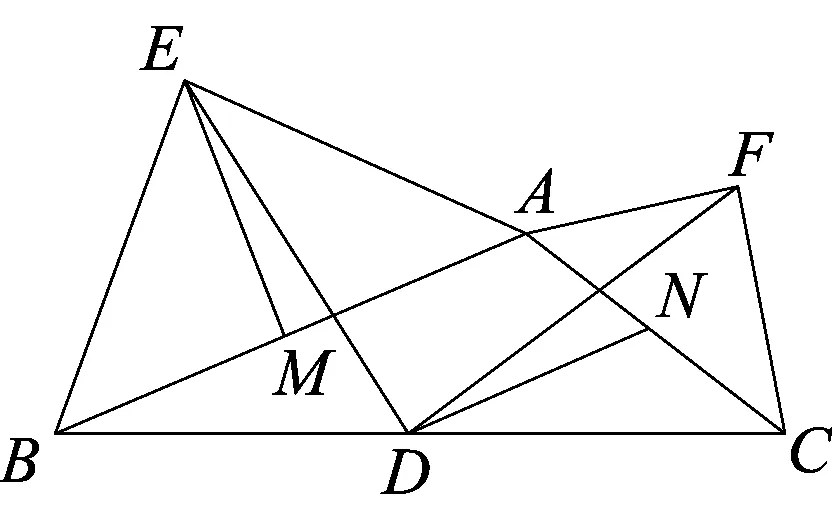
图4
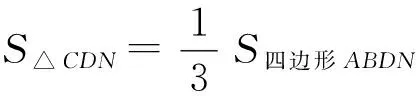
A.1个 B.2个 C.3个 D.4个
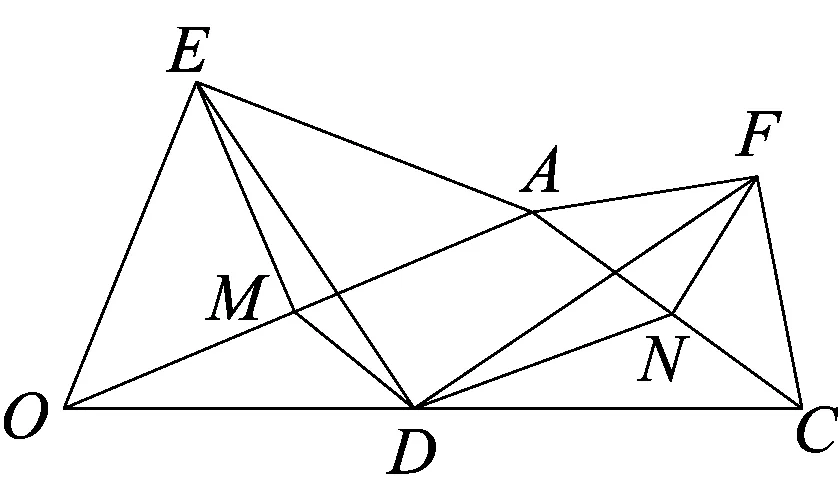
图5
(2016年安徽“合肥十校”联考数学模拟(一)第23题)如图5,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
这两题都是以钝角三角形的边为斜边向形外侧作等腰直角三角形,考查等腰直角三角形的性质(两个锐角都是45°,斜边上中线、角平分线、斜边上的高三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径)和应用、三角形中位线定理的应用、全等三角形的判定和性质的应用,平行四边形的判定和性质,以及相似三角形的判定和性质的应用等.
3 试题剖析
2016年安徽中考第23题,在钝角的边上截取两条线段(依然钝角三角形),以两条线段为斜边向角的外部作等腰直角三角形,将两个等腰直角三角形斜边上的中线延长,建构新图形,由相似三角形出发探究角的度数和线段的比值,给问题的求解增添了难度,焕发“旧题赋新意,老树开新花”的效果.
第(1)问,根据点C、D、E分别是OA、OB、AB的中点,可得DE、CE是△AOB的中位线.根据三角形中位线的性质得到DEOC,CEOD,推出四边形ODEC为平行四边形,于是得到∠OCE=∠ODE.由△OAP与△OBQ都是等腰直角三角形,根据等腰直角三角形的定义易得,由全等三角形的判定方法即可证明△PCE≌△EDQ.
显然,有效的解题不能单纯地依靠模仿和记忆,而是应该通过观察、猜想、验证推理等数学活动,形成自己对数学知识的理解和掌握.使知识内化,方法获得迁移,能力得以提升,因此,教学中锤炼解题思想方法,积累解题经验尤为重要.
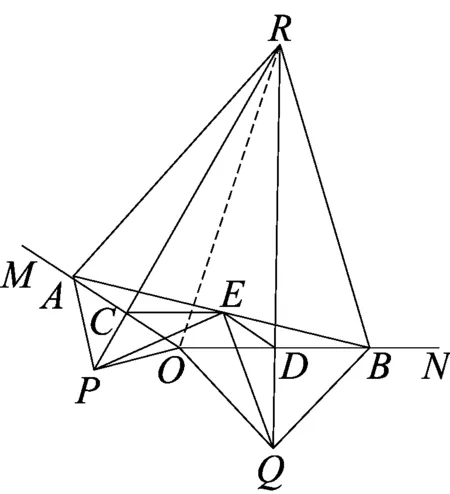
图6
第(2)问①如图6,连接RO,根据PR与QR分别为线段OA与OB的垂直平分线,得到AR=OR=BR,由等腰三角形的性质得到∠ARC=∠ORC,∠ORD=∠BRD.在四边形OCRD中,由∠OCR=∠ODR=90°,∠MON=150°,可得∠CRD=30°,进而得∠ARB=60°.由“有一个角是60°的等腰三角形是等边三角形”得△ABR为等边三角形.
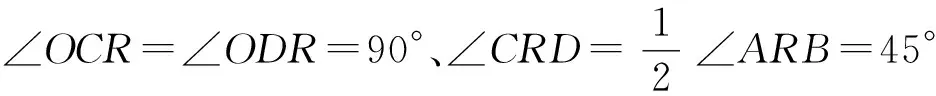
通过分析,不难发现该题考查等腰直角三角形的性质、直角三角形斜边上中线的性质、三角形中位线的性质、平行四边形的判定及性质、全等三角形的判定、“三线合一”性质、线段垂直平分线的判定及性质、四边形内角和及等边三角形的判定(有一个角是60°的等腰三角形是等边三角形)、相似三角形的判定及性质等.图中线多干扰视角,影响思考.全等条件(特别是角)隐藏图中,需认真观察、仔细分析、多方探寻.无线段长度,求线段比值等令人心发慌.可熟悉的题型与图形又给人“似曾相识燕归来”之感.此情此景又会让人“有法可想、有口可入、有路可走”乃至“有利可图”,只要有所思、有所想、有所悟,各种思维、思想、方法和灵感便会引爆,进而解决问题.
4 试题引发的思考
鉴于上述剖析,可以看出面对这种难题,靠考场上的灵机一动,计上心来,或靠总复习时的突击就想解决,显然不太靠谱.立足数学核心概念,关注基础知识和基本技能;强调数学思维,关注数学学习过程;基于试题研究,积累解题经验是解决这些难题比较好的策略.
4.1 立足数学核心概念,关注基础知识和基本技能
数学核心概念是数学知识结构中的“联结点”,也是“生成”其他数学知识的基础.立足数学核心概念,把握数学问题本质,是理解数学知识,解决数学问题的关键.针对“图形与几何”学习内容,考查学生基础知识和基本技能的达成情况,主要是借助基本图形:三角形、四边形和圆,考查学生对重要几何基本事实的理解和运用,考查图形的性质及图形变化,考查学生在具体情境中合理应用图形的性质及判定解决问题的能力.因此,首先,强调基础知识落实.以教材为载体,以几何概念的内涵和外延为重点,理解概念所蕴含的数学思想方法,避免死记硬背概念,避免片面追求“偏题、难题、怪题”.关注教材中的例题、习题的落实,力求大多数能坚持正常数学学习的学生达到基本要求.其次,帮助学生构建“核心概念”之间结构体系,形成知识网络,通过变式训练,提炼基本图形等促使学生掌握应用图形性质及判定解题的基本技能,提升解决数学问题的水平.
4.2 强调数学思维,关注数学学习过程
有的同学做题又快又准,有的同学总能用最简单的方式来解题,有的同学总出现这样那样的问题,比如,时间不够用、考场上卡壳以及会做的题得不了满分……. 显然“思维”决定着考试的节奏和成绩. 何为思维呢?思维就是指人脑利用已有的知识对记忆的信息进行分析、计算、比较、判断、推理、决策的动态活动过程.它是获取知识及运用知识求解问题的根本途径.数学思维就是数学基础知识在更高层次上的抽象和概括,它蕴涵于数学知识之中,是数学知识的精髓.
由此我们得到:在复杂问题的解决时,要善于在众多条件和信息中有方向性的选择有用信息,形成新的判断和认识.不时地提出问题,甚至是假设或猜想,明确问题所在,由问题引导思考,进而解决问题,让学生经历“观察、实验、比较、归纳、猜想、推理、反思”等理性思维活动过程,优化思维品质,这对提升解题能力是十分有价值的.
4.3 基于试题研究,积累解题经验
中考试题通常是以教材例习题或其他省的中考题为“背景”,经过命题专家的巧妙构思编拟而成的,它们源于教材,又高于教材;源于原有考题,又高于原有考题.这就启发我们在教学中,要充分发挥教师的教学智慧,遴选教材中内涵丰富的典型例习题或其他省的典型中考试题,由浅入深,由此及彼,引导学生努力探索问题的衍生点,从题设、结论图形结构等方面多角度探究与联想,变式与拓展,挖掘内在的教学价值,发挥其辐射功能,创造性地使用教材,巧妙的引入中考题,开发丰富有效的课程资源,引导学生进行探究性学习,让学生感受知识的生成和发展的过程,在例习题及中考题的探究中洞察问题本质,在理解的基础上寻找知识的“生长点”,思考、归纳,从复杂图形中剥离出基本数学模型(基本图形),激活数学思维,通过解题与联想把蕴含其中的数学思想方法揭示出来,挖掘出隐含问题的本质属性.有效促进解题过程的思维定势正向迁移,化生为熟、化非常规题为标准题,为探索和发现基本模型积累数学活动经验.
著名数学教育家波利亚曾形象地指出:“好问题如同蘑菇,它们都能成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个.”平时,要善于寻找波利亚所说的“蘑菇群”,积累解题经验,努力实现“做一题”、“会一类”、“通一片”.
1 范宏业.透视中考压轴题 反思学习与复习[J] .中学数学研究,2014(12):45-48
2 王锋.积累解题经验 提升创新能力[J].中国数学教育,2013(10):30-33
3 刘金英,张义民,王立明.中考数学试题分类解析(二)[J].中国数学教育,2011(1-2):46-57
4 庄士忠.相似三角形中三等角题型一般解答方法及应用[J].中学数学杂志,2012(4):37-39
2016-08-26)

