视角有异 素养有别——由两年平面向量高考题引发的思考

浙江省平湖中学

李学军 (邮编：314200)



视角有异 素养有别
——由两年平面向量高考题引发的思考

浙江省平湖中学

李学军 (邮编：314200)

作为数学教师应该要研究解题，要研究学生的解题，引导学生用数学的思维来思考和解决问题，去体会、去体验在解题过程中的纠结和成功之后的快乐，实现真正意义的数学学习，结合浙江省2013年和2016年的两道平面向量试题进行对比、分析，归纳提炼出两道高考试题的共性，体会数学本真解题的历程，在这个过程中历练、提升学生的数学素养.

高考题；对比；视角；素养

1 问题的提出

学生在做数学题的过程中，大多数是寻找曾经做过的题目的味道，对于呈现他们面前的数学试题，不能很好思考试题的根本考点，考查的基本数学方法，当在遇到陌生的数学试题时，有时候就有一种无助的感觉.当遇到暂时无法入手试题的时候，我们是否真正的想到了数学学习的本质，真正想起了用数学思维去思考需要解决的问题.章建跃也曾说过：“要让学生养成‘回到概念去’思考和解决问题的习惯”.作为一线教师，笔者认为在平时的教学过程中，更应该关注数学学习的本真，用数学思维去思考数学问题，用多方位的视角去看待数学问题，能够提升多角度思考问题和多方位解决问题的能力，下面以浙江省 2013高考试题和浙江省2016年高考试题为例进行对比解题，把对这两道试题的思考历程呈现如下.

2 试题呈现

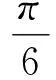
2.1 从坐标的视角出发，培养学生数学运算的能力

数学运算是数学活动的基本形式，也是演绎推理的一种形式，是得到数学结果的重要手段.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程.浙江省的这两个平面向量问题，要解决的都是最值问题，解决最值问题常规的办法通过构造函数或者构造不等式进行解决，而题目当中没有展示出这样的等式，因此，需要我们想办法，找出等式，然后进行数学运算，进而达到解决问题的目的.

解析 (2016年浙江卷理科第15题)

设a=(1,0),b=(2cosβ,2sinβ),e=(cosα,sinα)，

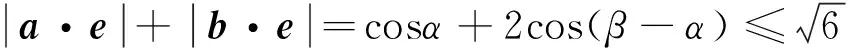
把α看成是主元，β看成是字母参数，所以

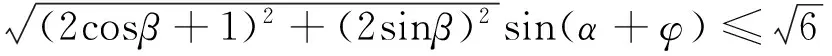
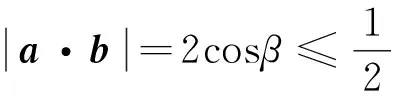
解析 (2013年浙江卷理科第17题)

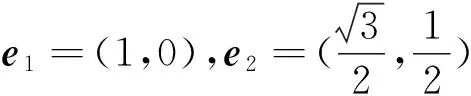
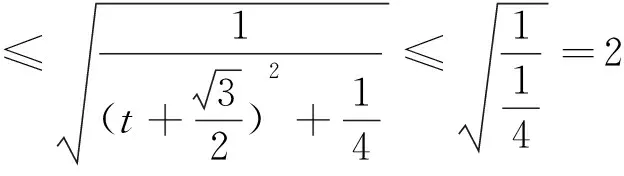
视角反思 利用坐标法来解决平面向量问题，实际上就是把抽象的向量问题转化为坐标运算，这种解法对于学生来说，“痛处”在于如何恰当地建立平面直角坐标系，整理出关系式，通过建立直角坐标系，引进两个变元已经让一部分学生感觉心生怯意了.接下来的数据处理存在一定转化和化归的技巧，2016年的考题是求最大值，通过分析两个向量的夹角应该是锐角，因此对夹角的限制减少了很多麻烦.要研究的最大值问题，因此把哪一个角看成主元是一种思维上的提升.2013年的考题也具有同样的特征，二元变量到一元变量的转化也使一部分学生的无法掌握并且熟练运用，第三层操作的障碍就是函数最值的处理，总体说来，这种解法对于学生来说困难重重，算对更不易.在这种数学运算核心素养的形成过程中，学生能够进一步发展数学运算能力，能有效借助运算方法解决实际问题，能够通过运算促进学生思维发展，养成程序化思考问题的习惯，形成一丝不苟，严谨求实的科学态度.

2.2 从代数的视角出发，培养学生逻辑推理的能力

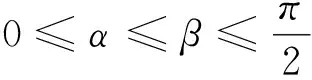
逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程.逻辑推理是得到数学结论，建构数学体系的重要方式，是数学严谨性的重要保证，是人们在数学活动中进行交流的基本思维品质.两个平面向量问题给出的是一种代数形式，利用代数变形处理向量问题也是解决平面向量问题的一种重要手段.在这个问题中，我们要从平面向量的两个基本要素着手，即平面向量的模和夹角来表示.因此，我们从这两个向量要素的视角入手，进行思考，把平面向量的相关最值问题转化为两个基本要素的关系，从而实现问题的完美解决.

解析 (2016年浙江卷理科第15题)

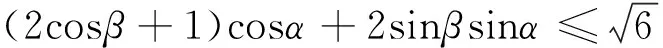
把α看成是主元，β看成是字母参数，

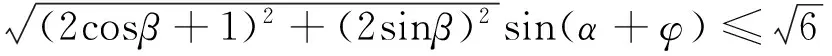
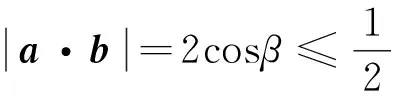
解析 (2013年浙江卷理科第17题)

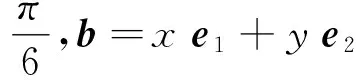
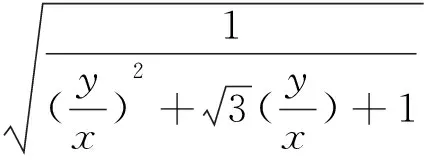
视角反思 两年的考题都是考查长度之间的关系，在平面向量中，真正反馈出长度的关系式，再从关系式入手，对于给出同样的代数式，观察的角度不同，就一定会产生不一样的想法.对于2016年的考题得出的是关于两个变元的不等式，对于2013年的考题得出的是关于两个变元的等式，这两年考题的核心实际上是函数，对于处理双变元的函数问题的化归就是想办法进行减元，这个转化是非常关键的，接下来的解法同上.在逻辑推理核心素养的形成过程中，学生能够发现问题和提出问题，能够掌握推理的形式，表述论证的过程，能理解数学知识之间的联系，建构知识框架，形成有论据、有条理、合乎逻辑的思维品质，增强数学交流能力.学生通过代数视角的思考，透过问题的主旨、背景，向相似的、相关的数学问题进行辐射，逐步引导学生去悟，直到学生自发地悟，形成自己的解决问题的能力和解决问题方法.

2.3 从几何的视角出发，培养学生直观想象的能力

直观想象是指借助几何直观和空间想象感知事物的形态和变化，利用图形理解和解决数学问题的过程.直观想象是发现和提出数学问题、分析和解决数学问题的重要手段，是探索和形成论证思路、进行逻辑推理、构造抽象结构的思维基础.平面向量是代数和几何的纽带和桥梁，因此，完全可以通过几何意义，构造出相应的几何图形，通过图形进行数形结合最终实现解决问题的效果.

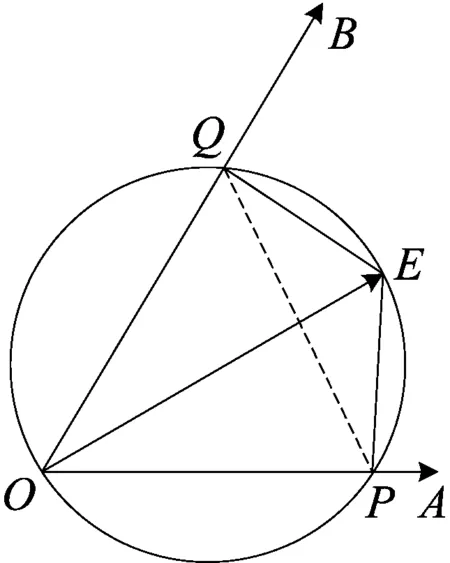
解析 (2016年浙江卷理科第15题)

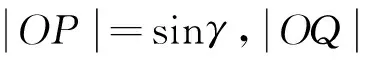
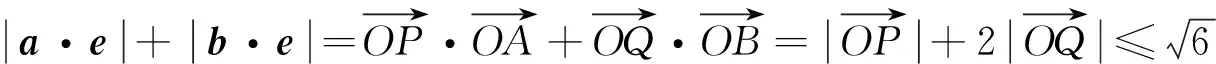
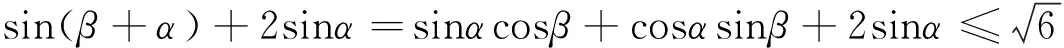
下同解法1

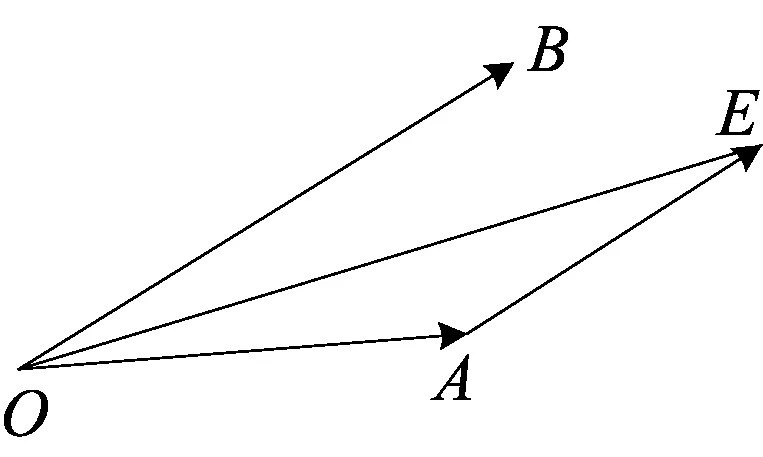
解析 (2013年浙江卷理科第17题)

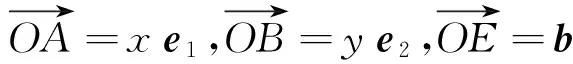
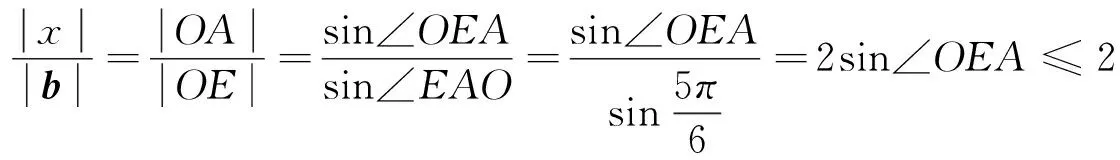
视角反思 平面向量本身具有代数和几何的双层特征，因此在解决这两年考题的过程中，试图从形的角度进行思考.对于那些几何背景素养较高的学生来说，结合平面向量的几何背景入手，可以先从一些特殊的图形入手，然后进行归纳分析，从而提升出得到最值的状态.对于2016年的考题来说，通过画出一些图形分析得到的是圆中的问题，从而从圆的角度入手分析，从而使得比较抽象的问题转化为实实在在的平面几何问题；对于2013年的考题，就是三角形中，已知一个内角，另一个角在变化，研究这两个角的对边之比的最值问题.但是对于学习数学来说，不要忽略数学当中非常重要的数学思维，即归纳-猜想-论证.归纳至少要有三个数据，因此我们要想办法找到这些数据，有这样的思维方式，找的数据越多越容易归纳出结论，然后就比较容易进行论证.这样的处理问题的方式在平时是缺少训练的，而这种方式却能很好地避开繁琐的计算.在直观想象核心素养的形成过程中，学生能够进一步发展几何直观和空间想象能力，增强运用图形和空间想象思考问题的意识，提升数形结合的能力，感悟事物的本质，培养创新思维，这也正是我们教师所希望看到的.

2.4 从构造的视角出发，培养学生数学建模的能力

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.数学模型构建了数学与外部的桥梁，是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段，是推动数学发展的动力.这两道平面向量问题结合我们高中的数学知识，长度之间的关系融入其中，进行建构恰当的数学模型，通过必要的转化和化归，从而实现解决问题的捷径.

解析 (2016年浙江卷理科第15题)

解析 (2013年浙江卷理科第17题)

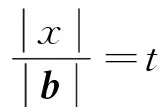
视角反思 数学家克莱因说过：“教师掌握的知识要比他所教的知识多得多，才能引导学生绕过悬崖、渡过险滩.”对于浙江省两年的数学考题中的平面向量考点的共性除了上述通性通法之外，也可以通过构造法进行解决.如2016年的考题，通过构造三角不等式，三角不等式就是来源于几何图形，在这当中之所以隐蔽，比较难考虑到这种方法.我认为，主要还是陷入到平面向量的考点当中，正所谓当局者迷；还有一个原因，应该是平时三角不等式的使用频率不高，也就是不够熟练或者说是盲点.对于2013年的考题，对于代数式的变形是比较困难的，原因就是只可以在分子和分母之间进行恒等变形，如果可以构造出等式或者不等式，变形的途径就不仅仅在分子和分母的变形这么单一了.思路瞬间拓宽了很多，可以左右进行恒等变形，分式到整式等都是信手拈来.此法是通过引入参数t建立方程，进而转化为求参量t的最大值的问题.难点是如何“减元”，如何把多变元问题转化为单变元问题，从而利用一元二次方程有解的思想构造不等式，利用判别式法求出参量t的取值范围.在数学建模核心素养的形成过程中，积累用数学解决实际问题的经验.学生能够在实际情境中发现和提出问题，能够针对问题建立数学模型，能够运用数学知识求解模型，并尝试基于现实背景验证和完善模型，能够提升应用能力，增强创新意识，这也真正体现了高考的选拔人才的目的.

通过上述解题视角的分析和理解，笔者尝试了对2016年的考题进行了如下的改编，提升对此类问题的理解与感悟.

改编赏析：

在解决问题的过程中，解题的思路是如何形成的，解题的方法是如何构想的，这些对于学生来说都是至关重要的疑问，应该留给学生足够的反思时间和“悟透“的空间.反思解题方法的探索发行过程，反思错误的成因及对策，反思处理问题的思维过程和数学思想方法，反思是否对问题进行深入细致的分析转化.学生通过回顾和总结解题思路的机会，一定能够收到事半功倍的效果.

3 结束语

学生通过一段时间的有计划的、有目的的、“多角度多视角”打磨之后，会对所探究过的题目产生一定的想法，会对相似的进行串联.通过一定的时间训练，学生会对题目之间多一些“为什么”、“怎么样”的观念，给学生一个机会，学生会给教师一个“精彩”.伟大数学家哈尔莫斯曾说过：“问题是数学的心脏”.数学的学习就是在不断的提出问题和解决问题的过程中发展的.波利亚也说过：“掌握数学就意味着善于解题，不仅善于解一些标准的题，而且善于解一些要求独立思考、思路合理、见解独到和有发明创造的题”.学生在数学学习的过程中，领悟基本知识、基本方法的运用，通过引导学生归纳解题方法、技巧、规律和思想方法，促进知识向能力转变，实现自我完善.争取做一题通一法，会一类通一片的效果，让“思考视角”在我们的数学教学中发挥应有的锻炼.

美国著名作家海明威曾经谈到过“冰山理论”，他认为人们看到的小说只是冰露在海面上的八分之一，那海面下的八分之七得让读者自己去体会揣摩.我们的数学教学又何尝不是这样的呢？数学教育家波利亚也指出：“中学数学教学首要的任务就是要加强解题的训练.”在数学的解题过程中，数学的思想方法是解题之魂.有什么样的思想方法就会产生什么样的解法，而在数学教育中不可回避的数学解题的视角，恰恰可以引领我们产生“神奇”的想法，通过教师的正确引领，学生的顽强训练，我们的学生在数学学习的舞台上一定能够充满激情的、自信的奔跑！

1 卢明.稳中求变 体现创新[J].中学教研(数学)2015(8)

2 吴冠男 沈新权.微过程 深反思[J].中学教研(数学)2015(9)

3 李学军.用本促真 贴地前行[J].中学教研(数学)2016(4)4 李学军.观千剑而后识器[J].中学教研(数学)2016(8)

2016-09-06)