回归自然 领悟本质
——对等差数列前n项和公式推导教学过程的思考
中国科技大学附属中学
黄严生 (邮编:230051)
聚焦新课程
回归自然 领悟本质
——对等差数列前n项和公式推导教学过程的思考
中国科技大学附属中学
黄严生 (邮编:230051)
很多老师受高考指挥棒的影响,急功近利.对数学公式原理教学,没有很好落实数学原理教学原则,不注重知识形成、发展过程.对公式的推导过程大而化之,在例题讲解和习题训练上,不惜花费大量的时间,这种做法看似效率很高,学生应用能力有所提高.其实不然,学生的这种解题能力提高是暂时的,是模仿性质的,学生对原理、公式的理解是肤浅的,对原理、公式所蕴含的思想方法都知之甚少.
教师的课堂教学,实质上是落实如何学的问题,教师的教是为了学生的学. 爱因斯坦说,“唤起独创性的表现与求知之乐,是为人师者至高无比的秘方”. 教师不是简单地告诉学生做什么,而不是向学生解释怎么做,应是激励学生去观察、思考、顿悟和发现. 因此,教师要弄清教什么、如何教、怎么教,才能更好地落实学生学的问题.本文以等差数列前n项和公式推导为例,从以下几个方面进行分析,供大家参考.
1 案例透视与评析
人民教育出版社普通高中课程标准实验教科书《数学》必修5,2.3节的内容是“等差数列的前n项和”,教材中利用高斯加法作为引例.下面是一位教师推导“等差数列的前n项和公式”的教学片断:
问题1 请大家计算:1+2+…+100=?
由于不少学生在小学时就学习过高斯加法,学生利用高斯加法很快解决上面的计算问题.即1+2+…+100=(1+100)+(2+99)+…+(50+51)=101×50=5050.
问题2 你们能计算1+2+…+100+101吗?
学生1:1+2+…+100+101=(1+101)+(2+100)+…+(50+52)+51=102×50+51=5151.
学生2:1+2+…+100+101=(1+2+…+100)+101=5050+101=5151.
教师:很好,同学们能利用高斯加法思想或用以前已经解决问题来解决上面的求和问题.
问题3 请大家计算:1+2+…+n(n∈N*)
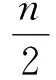
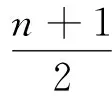
问题4 请大家思考还有没有其他方法解决问题3的计算?

教师:学生4用的也是转化方法,当n是奇数时,通过添加一项n+1,将其转化偶数的情形进行计算.
问题5 你们还有没有其它方法计算?
学生感到茫然,大家认为,除分类外,好像找不到更好的方法.此时教师没有急于求成,而是引导学生,积极地退回去,反思回顾上面的计算方法,并留足时间让学生观察、思考,从中发现问题本质.使学生逐步感悟到,不论是哪种方法,其本质就是将不同数转化为相同数求和.教师可以进一步追问,既然如此,那么我们能否避免用分类讨论方法解决呢?上面的方法都是从算式和内部结构出发,通过分类转化,达到求解目的的.我们的思维能不能跳出来,能否对算式进行再创造呢?(留足时间让学生思考)
学生5:可以重新构造一个求和问题,计算n+(n-1)+…+2+1,于是


教师:学生的方法就是倒序相加求和法,通过倒序相加,能将复杂的求和问题转化为简单的求和,即转化为n个n+1的和.
问题6 请大家自己推导等差数列的求和公式.
学生自主探究,求等差数列前n项和的方法---倒序相加求和法,推导出等差数列前n项和公式.

2 重温高斯加法,让知识生成更自然
数列的求和问题,实际上就是一种加法运算.但学生在此之前对多个数的求和问题,接触不多.既然出现了认知冲突,那么如何解决,如何引导学生利用已有知识去同化或顺应新知识呢?维果斯基的“最近发展区理论”认为,学生的发展有两种水平:一种是学生的现有水平,指独立活动时所能达到的解决问题的水平;另一种是学生可能的发展水平,也就是通过教学所获得的潜力.两者之间的差异就是最近发展区.教学应着眼于学生的最近发展区,为学生提供带有难度的内容,调动学生的积极性,发挥其潜能,超越其最近发展区而达到下一发展阶段的水平,然后在此基础上进行下一个发展区的发展.
2.1 对高斯加法的再认识
数列的求和就是解决多个数相加的问题,因此,学生现有能解决数列求和的知识,只有实数的加法、乘法的运算法则及其意义.
高斯加法的本质是,根据加法的交换律将加数进行配对,于是1+2+…+100=(1+100)+(2+99)+…+(50+51)=50×101.
这一过程是将其转化为50个101相加,将不同数的求和问题,转化为相同数求和问题,利用乘法意义,即可求出1+2+…+100的和等于101×50.这种由加法运算,过渡到乘法的运算,是一种飞跃,是一种突破.也就是利用已有的知识能力,解决一个全新的问题,是新课程理念所倡导的.
2.2 高斯加法思想的应用
乘法的意义是求n个相同数a的求和的运算,即n个a相加,记为n×a.乘法的意义实际上是解决了相同数的相加问题,加法的交换律和乘法的意义是高斯加法的理论依据.这些知识虽然是基础,但在学生脑海中是沉睡的知识.虽然每天都在不自觉地运用着,但要学生有意识地调用这些知识来解决新问题,却没有这种习惯,有一定的难度.实际上,每个数学问题的解决,都要运用与之相关的一系列数学知识作为理论依据,进行推理论证和演算.因此,如何唤起学生,检索、调用贮存在大脑中的知识来解决新问题,是教师教学的艺术.
教师可以提出一些问题去刺激、去激发学生思考,激活学生大脑中的知识,用于解决问题.因此,在探究高斯加法时,可以设计一些问题.如:我们解决过多个数的求和问题吗?你知道哪些?如何求?
通过问题引领,学生顿时觉得豁然开朗,体会到数学既是深奥的,也是简单的.学生已有的知识,加法运算、加法的交换律、乘法的意义得以充分调动,深知这些知识是解决1+2+…+100的求和的理论工具,是知识的最近发展区,分组、合并同类项解决问题基本方法.学生有了这种认识,对于1+2+…+100+101的求和,也就得心应手,不难解决.自然会产生如下的思维方法:
(1)1+2+…+100+101=50×101+101;
(2)1+2+…+100+101=50×102+51;
(3)1+2+…+100+101=1+2+…+100+101+102-102=51×103-102.
评析 (1)利用已求的1+2+…+100的和来解决1+2+…+100+101的和,将分为两组(1+2+…+100)+101;(2)将加数51单独考虑,也是分为两组,即
(1+2+…+50+52+53+…+100+101)+51=50×102+51;(3)将原式增加一个数102,转化为偶数个数相加,利用高斯加法思想顺利解决问题.
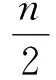
以上处理问题的方法,不论如何变化,最终目的是转化为偶数个数的和,通过配对转化为相同数的求和问题.
2.3 倒序相加的形成过程
能否找到一个通用的方法,既能解决是n的偶数情形,又能解决n是奇数情形的问题呢?显然,当n是奇数时,只从1+2+…+(n-1)+n是无法得到的.在学生思维出现暂时阻滞时,不要简单告知,让学生回顾、反思上面的思维过程,是如何将其转化为乘法运算,进而,将解决问题方法进行迁移.经过探究讨论,学生发现,由于n是奇数,从原式的结构上看是无法实现的配对分组,要想实现分组配对,必须将1+2+…+(n-1)+n进行加工构建,转化为偶数个数的和.经过学生讨论、交流,发现在原式上再加一个1+2+…+(n-1)+n后,得到求2n个数的和问题,因此,就能顺利将它们分成n组(i+(n-i+1),1≤i≤n,i∈N*)),即可以化为n个(n+1)的和.
这样倒序相加法不是教师告知的,而是在解决问题中自然生成的,是学生在问题探究中自我发现的一种解题方法.倒序相加法是解决某类问题一种技巧,技巧本身不重要,重要的是这种探究过程、获得数学方法的思维过程.
2.4 抓住本质,领悟思想
另外,笔者听了很多节该课题的课,授课教师在介绍高斯加法后,都如出一辙地让学生利用倒序相加方法推导等差数列的前n项和公式,这也是教材中介绍的方法. 机械模仿式学习、训练弊端是毋庸置疑的,仍没有引起一些教师的注意,倒序相加求和法所蕴含的数学思想方法没有真正被揭示.教师在教学中过分强调倒序相加求和法的运用,这样易形成思维僵化,不利于培养学生的创新思维.
如果学生没有深刻理解高斯加法的本质,如“计算1-2+3-4+…+(-1)2n-1×2n的和”等问题,学生就会不知所措.学生只要善于分析、观察,就不难发现其中的规律,就可以将1-2+3-4+…+(-1)2n-1×2n分成n组,即第一项与第二项分为一组,第三项与第四项分为一组,…,第2n-1项与第2n项分为一组,分成n组,每组的和都是-1,于是1-2+3-4+…+(-1)2n-1×2n=-n.

等差数列前n项和公式推导过程,概括起来说就是重构分组,通过学生大脑中新旧知识的相互作用,实现化归.将不会的问题转化已经解决问题进行处理,或者将复杂问题转化为简单问题,这就是本质,也是数学思维的精髓.数学公理、定义、定理与证明必须作为一个活跃的成分,渗透于推理过程之中.学生必须主动地去发现、学习、组织、检验并使用它们.由于数学知识是数学家思维活动的成果,他们的思维方法和思维过程是学生思维活动的典范,他们的思维是通过文本和教师的加工处理来影响着学生的思维.因此,在教学中,对公式原理的教学,要重视原理、公式本身的数学价值,很好地去发掘数学原理、公式形成过程中数学家的思维活动.摒弃将结果直接呈现给学生,通过大量的例题讲解和习题训练,来巩固和加深理解.其实,原理、公式本身就是经典的例题,我们应该充分用好和发挥好原理、公式的教学功能.
3 寄语
“教员不是拿所得的结果教人,最要紧的是拿怎样得到结果的方法教人”. 毕达哥拉斯说,“在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么.”因此,在教学中,如何将教材呈现的知识进行再创造,通过问题链激发学生思维,揭示知识所蕴含的数学思想方法,通过教师的引导,让学生在数学学习过程中,经历获得数学公式的思维活动经验.这样学到的不是单个的知识点,而是培养了获取新知的能力.至于某个知识点,经过一段时间以后可能遗忘,但这种理性思维的精神将终生难忘.同时,从方法论和发现论看,为日后学习、获取知识、发现问题、创新地提出问题,以及研究问题方法和解决问题思路都有借鉴,如何化未知为已知,化陌生为熟悉,化复杂为简单,做到大道至简,将是终生受益的.
1 中华人共和国教育部.普通高中数学课程标准(试用)[M].北京:人民教育出版社,2003
2 丁益民.例谈数学家思维的教学功能[J].数学通报,2016(5) : 15-17
3 [美]G·波利亚.怎样解题[M].上海:上海科技教育出版社,2007新一版
2016-09-26)

