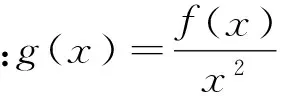基于MPCK视角下的解题反思
——以“一道月考试题”为例
福建省厦门市第一中学
王淼生 (邮编:361003)
基于MPCK视角下的解题反思
——以“一道月考试题”为例
福建省厦门市第一中学
王淼生 (邮编:361003)
舒尔曼1986年提出PCK(学科教学内容知识)理论后,立即引起各国学者关注,从而使数学教师特有的学科教学知识从PCK泛学科的研究中独立出来,形成MPCK(数学学科教学内容知识)理论.MPCK要求数学教师面对特定问题时,反思学生遇到困难的原因并采取有效教学策略,构建高效的解题教学,这是MPCK理论在解题教学中的应用.本文基于MPCK理论,从哲学观点来反思一道月考试题解答过程,不妥之处,敬请批评指正.
1 真题呈现
前不久月考中出现这样一道试题(下称案例1):
(I)若函数f(x)在定义域上不单调,求实数a的取值范围;

2 全军覆没
案例1是最后一道压轴题,全年级没有考生能够真正完整解答,全军覆没,令人痛心.那应该怎样解答呢?
对于(II)对函数求导可得
由题意可知x1、x2是以下方程的两个不等正根(不妨设x1 f′(x)=0⟺x2-ax+1=0. 据韦达定理可得 x1+x2=a,x1x2=1. ① 由两点斜率公式可得 ② ③ 据已知条件可得 ④ g(x)≤g(e). ⑤ 以下来研究函数g(x)的单调性(即图象走势),显然最有效的方法就是求导: ⑥ ⑦ h(x) ⑧ 数学教育家波利亚在文[1]“解题表”中指出数学解题过程分为弄清问题、拟定计划、实施过程、回顾反思等四个阶段,其中最重要也是最容易忽视的就是解题后的反思.解题教学的核心在于反思,怎样反思、反思什么是衡量解题教学效率高低的杠杆.正如著名的特级教师任勇在文[2]中感叹:“如果求出了问题的答案就匆匆合上作业本,我们将失去做这道题本来应该得到的更多、更宝贵的东西.光解题而没有反思就如同入宝山却空着手回来.” 3.1 反思之一:唯物辩证的观点 罗增儒教授在文[3]指出,尽管数学试题千变万化,但深入研究还是具有一定规律,教师就是指引学生寻觅这些规律的“领路人”.有关导数综合试题,几乎都有这样的规律:构造新的函数φ(x)后,都能将问题转化为“φ(x)≥(≤)φ(t)”的结构,然后证明φ(x)的单调性.借助这一特点往往收到意想不到的奇效,甚至起死回生,比如上述⑤、⑧. 数学解题应遵循规律,也需要一定模式,但过度强调并套用固定模式则会思维僵化.不少学生总认为上述表达式②应该凑合成“齐次”形式,而此题难以实现,故而束手无策,这是本题失分的第一个原因.亦有部分学生因套用模式,即强行凑成“齐次”而导致结构复杂,尤其是求导过程极其繁琐而不得不中途停止,前功尽弃,这是本题丢分的另一个原因. 3.2 反思之二:整体与局部的观点 安振平先生认为代数变形能力是一个数学教师专业水平的重要标志.对于复杂的导数综合问题,求导之前应适当变形.尤其含有“lnx”,应该尽量将“lnx”前面的一切“分离”开来,比如从⑥到⑦就轻松避免了求导越来越复杂,这一看似简单的变形却是致命的.反之,若直接对⑥求导,不仅“lnx”永远不可能消失,而且每求导一次,结果愈加复杂,这是部分学生无奈放弃的原因. 表面上似乎⑦比⑥更加复杂,那为何还要这样变形呢?尽管⑦确实比⑥复杂,但我们聚焦不在⑦的“整体”上,而是在⑦的“局部”.因为我们只要判断⑦的符号,即只要研究上述目标函数h(x)符号,为此只要对h(x)再一次求导,问题就变得简单得多.遗憾的是全年级没有一名学生实施“分离”,为何要 “分离”呢?因为求导最终目的就是为了画出函数图形,即刻画图象大致走势.这就需要研究函数的单调性与极值情况,即判断导函数符号,当然渴望将导函数因式分解,进而求出极值点.上述⑥到⑦即“分离”之后,通过求导将原来的“lnx”转化为关于x的多项式,为实施因式分解带来极大方便.而含有“lnx”就难以实施因式分解,就不可能求出极值点,这是极少数学生坚持到最后而痛失分数的原因所在. 3.3 反思之三:普遍联系的观点 目前课堂解题教学一味追求数量,忽视质量,缺乏反思,导致学生过后依然还是“涛声依旧”.因为学生不知道错误的原因,更不清楚破解试题的突破口与关键点在何处,因而还是无法独立完成此类试题.于是教师再一次更加密集地训练、更加频繁地考试、更大数量地讲评,这种一轮又一轮加码循环,愈演愈烈.学生陷入题海苦不堪言,教师唉声一片伤了自己.反复折腾,学生怎么可能对数学感兴趣?怎么可能激发学生的创造力呢?波利亚感叹:“一个专心认真备课教师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个侧面,使得通过这道试题就好像通过一道门户,把学生引入一个完整的理论领域.” 案例1涉及的是与“lnx”相关求导问题,lnx与ex是一对“孪生兄弟”,即与“ex”相关的问题,同样也需要将“ex” 前面的一切“分离”开来,否则也会陷入同样的困境.巧合的是最近还遭遇到这样一道试题(下称案例2): 案例2 若函数f(x)满足x2f′(x)-2xf(x)=x3ex,f(2)=-2e2.则x>0时,f(x) ( ) A.有极大值,无极小值 B.有极小值,无极大值 C.即有极大值,又有极小值 D.既无极大值,又无极小值 解答如下:当x>0时,将已知条件变形为 f(x)=x2g(x) ⟹f′(x)=2xg(x)+x2g′(x)=2xg(x)+xex ⑨ ⑩ 依据⑩,再一次构造函数: h(x)=2g(x)+ex⟹h′(x)=2g′(x)+ex>0. x(0,2)2(2,¥)f'(x)-0+f(x)单调递减取得极小值单调递增 依据上述表格答案选B. 关于上述案例2,还有一个小故事:案例2作为选择题,没有具体解答过程,只有一个参考答案B.结果到了考试那天,备课组全体教师都觉得无法判断是否存在极大值而误以为是一道错题,在考试中途临时不得不更换一个题目.其实,案例2主要考查函数f(x)的极值情况,即需要对f′(x)实施因式分解,但因f(x)是抽象函数,故难以对上述⑨直接实施因式分解,于是再一次对上述⑨求导,结果发现越来越复杂,连教师自己也不得不终止运算,加上无法判断是否存在极大值,这就是绝大部分教师认为这是一道错题的缘故.此时,破解困境的关键在于⑨到⑩.事实上,从⑨到⑩仅仅只是“分离”了x,问题就立即变得简单明了,迎刃而解,而这恰恰是绝大教师没有发现的“秘密通道”. 由此可见,教师自己也经常犯这种“不分离”而“一锅煮”的错误.解题不是数学的全部,也不是数学教师业务水平的唯一标志.但数学教师离不开解题,解题能力直接影响其教学水平.没有强大解题能力,就不可能成为一流的数学教师.这从一个侧面印证了为何全国很多数学教师渴望参加中学数学教学参考主办的解题研讨,也解释了罗增儒教授名著《中学数学解题的理论与实践》火爆的原因.正如波利亚所言:“学习数学就是学习解题,掌握数学就意味着善于解题.”任何一位教师都希望不断地提高自己与学生的解题能力,因此,反思不仅提高学生解题能力,更有利于提升教师专业水平. 3.4 反思之四:量变质变的观点 其实,优秀解题高手(无论学生还是教师)与一般人的区别在于长期强调反思、关注细节、重视量变、把握质变.这种量的积累必然决定了试题解答最后成败往往在于关键某一步的实施,比如案例1中的⑥到⑦、案例2中的⑨到⑩“分离”步骤.正所谓反思铸就高度,细节决定成败,量变引起质变,质变回馈量变. 3.5 反思之五:主观能动性观点 新一轮课改首次将情感态度与价值观同知识和技能、过程和方法一起并列为基础教育的三维目标.尽管以前大纲也在不同程度上强调“情感态度与价值观”的重要性,但是新一轮课改,则把“情感态度与价值观”作为课程目标,这样“情感态度与价值观”不再是可有可无的东西,而是必须实现的基本目标.作为压轴的导数综合试题,通常具有较大的难度,这是一种正常现象.数学教育一个重要目的就是培养学生勇于探索、迎难而上的意志和毅力.没有坚强的意志,缺乏坚韧的毅力,是不可能学好数学,这正是新一轮课改将“情感态度与价值观”作为三维目标之一的缘由所在.值得指出的是,情感态度与价值观并非仅仅指向学生,教师也不例外.上述案例1、案例2的解答过程是笔者锲而不舍才得到,绝非一蹴而就,期盼读者呈现更加简捷的方法. 华东师大终身教授叶澜感叹:“一个教师写一辈子教案不一定成为名师,如果一个教师写三年反思就有可能成为名师.”反思是主观能动性突出表现,是辩证唯物主义在具体的数学学科的体现,更是对MPCK理论的完善和创新.依据舒尔曼的PCK理论,专家型教师与一般教师的根本差距就在于专家型通过反思使得学术知识、实施策略转化为学生易接受、易理解、易操作的教学知识和动手操作能力.MPCK理论不是虚无缥缈,更不是从天而降,而是主观能动性的表现,是 在实践中形成并在实践中得到升华,上述案例1与案例2正是PCK理论在解题反思中的具体体现和最佳诠释例证. 1 波利亚.怎样解题(阎育苏 译)[M].北京:科学出版社,1982 2 任勇.中学数学解题百技巧[M].福州:福建少年儿童出版社,1998 3 罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,1997 本文系全国教育科学“十二五”规划2015年度单位资助教育部规划课题“基于数学教学内容知识(MPCK)视角下的概念教学案例研究”(课题批准号FHB150464)研究成果. 2016-09-06)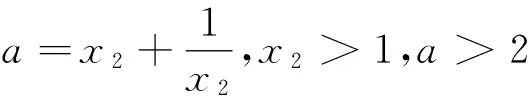
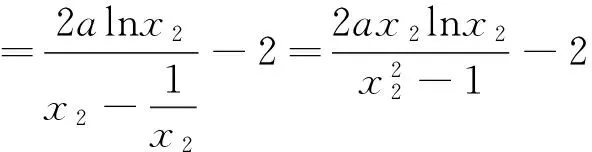
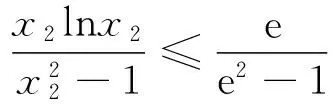
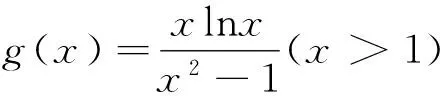
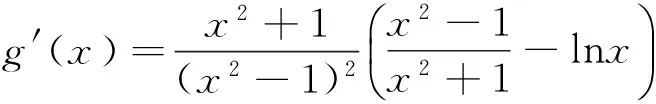
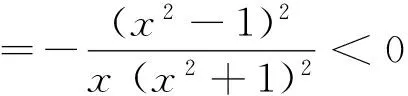
3 基于MPCK视角下的解题反思