数学物理方程某些相关理论和复变函数的发展

张一方

(云南大学物理系，云南 昆明 650091)



数学物理方程某些相关理论和复变函数的发展

张一方

(云南大学物理系，云南 昆明 650091)

摘要：首先，讨论了一般方程及其某些解的简化形式；其次，介绍了数学物理方程及其对称性；第三，研究了方程的不动点、定性分析理论和相应的各种应用；第四，由矩阵联系于线性代数；第五，讨论与数学物理相关的各种量；最后，探讨数域的推广和复变函数发展(各种超复变函数).

关键词：数理方法；方程；定性分析；线性代数；数域；复变函数

1一般方程

基于各种相互作用的规范理论，讨论了规范场方程的某些新的解及其与极限环、各种奇异点的关系，探讨了这些结果可能具有的粒子性质和相变等物理意义[1].笔者在复数、四元数等发展的基础上，提出了一种新的数系发展模式：四元数推广为矩阵形式aI+bA+cB+dC，其中单位矩阵I和3个特殊矩阵A,B,C分别相应于数1和虚数单位i,j,k.它们一般组成环，但3种矩阵aI+bA，aI+cB，aI+dC及某些特殊的二阶甚至高阶矩阵可以组成域，这是一类新的超复数系.还探讨了这种新数系可能具有的物理意义[2-3].同时讨论了数学分析中n个变量的对称性，微积分的对称性及其统一.然后推广微积分的阶数n等到分数及各种数系，由此得到某些新的结果及这些新探索的意义[4].当数学分析中的空间维数和微积分的阶数n等推广到分数及各种数系时，场论及其公式也可以相应推广.笔者研究了此时的Gauss定理、Stokes定理及相应的梯度、散度、旋度的推广，其中旋度可能有几种不同的形式，并探讨了这些结果在物理学中的应用[5].

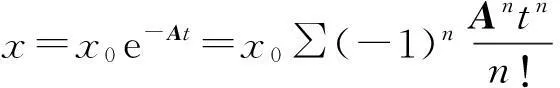
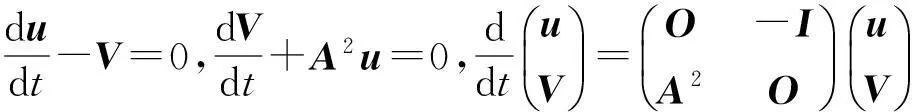
即

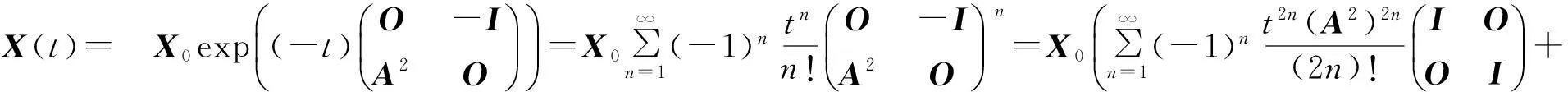
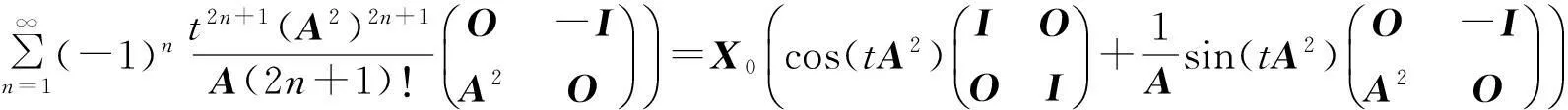
对高阶常系数线性齐次方程可以进行完全类似的推广.n阶方程可以化为n个方程组，对应n阶方阵.类似于此，三角函数、双曲函数等很多方程都可以化为级数解.

设方程组为

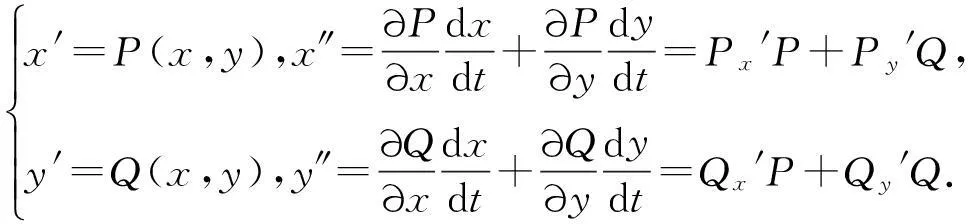
对于平衡点等，x″=Px′(x-x0)+Py′(y-y0)，则为高阶平衡点.

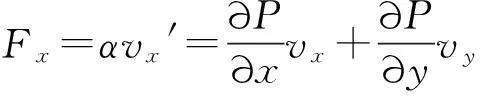
动量空间如果化为一般空间，可以结合力学，Poisson方程[qi,pj]=δij和Hamilton方程

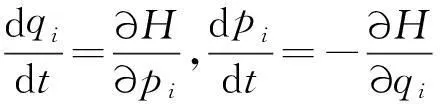
(1)

或结合量子力学xp-px=iħδ及其推广.

一般微分积分方程为

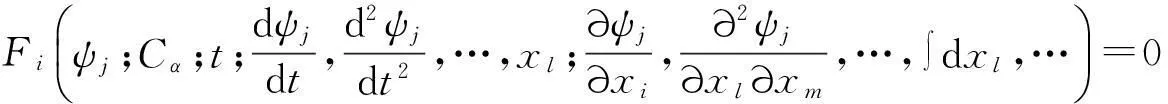
以下是各级简方程：

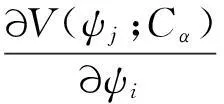
总之，对每一类方程的总性质都与一类群等相联系.每种数学运算都导致一种新类型的方程，如代数、微积分、差分等，因此微分、积分方程有所不同.对不同几何及统计学、概率论等各种数学分支都有相应的方程：代数方程表示解析几何的图形，微分方程表示微分几何的图形.任意一种数学式都表示一种相应几何的图形，而运算过程表示图形的变化，这也是数学基础，量、运算、形3方面的一种普适联系.

2数学物理方程及其对称性

通常二阶偏微分方程分为椭圆型方程、超双曲型方程和抛物型方程.在物理中，椭圆型方程对应位势方程，相应于稳恒场，描述状态，二次项全对称，导致定态Schrodinger方程；超双曲型方程对应波动方程，相应于波动场，描述过程，对称性有所破缺，导致Klein-Gordon(KG)方程；抛物型方程对应输运方程，相应于扩散场，描述过程，对称性完全破缺，导致一般Schrodinger方程.

相应椭圆方程解应该有所对称，并且所有稳恒场都有所对称，起码在高次项时，或方程一次项、常数项中x,y,z等对称时如此，如Poisson场.抛物型方程发展为虚数时就是Schrodinger方程，联系于波动方程.其余方程发展为虚数时各种方程及相应的场互相转化，如椭圆型方程(i)2=-1就是双曲型方程，反之亦然.复数i可以联系于相对论，而抛物型方程则是非相对论近似.

对相应的物理方程，波动方程描述各种周期性、波动性，包括经济、市场周期变化及人体节律等.热传导方程描述各种衰变、单向演化性、生灭，包括生态、人口及人体生长、衰老等.稳定场方程描述各种稳定性分布，如人体发育的相对稳定阶段.后二者各描述熵等的增大到稳定.它们在数学上各有对应，包括所有线性方程.

数学物理方程在球、柱坐标中一般归为Legendre和Bessel方程.方程本身推广时，在各种坐标系中，推广到n维空间时，还应该有各种特殊函数.目前的许多数理方程可以统一为Sturm-Liouville(SL)方程：

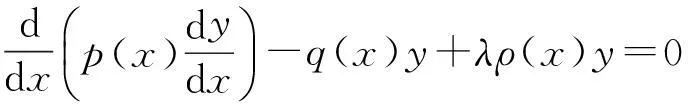
对每类方程，如SL方程，都可能有一类统一的通解.

Legendre方程、Hermit方程和Laguerre从方程形式上可以统一为q=0特殊的SL方程：

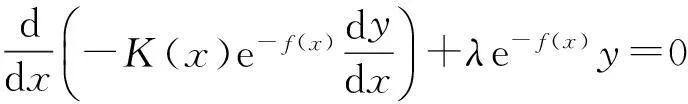
即Ky″+(K′-Kf′)y′-λy=0.其中K(x)是多项式，λ是本征值.已知Legendre函数的微分形式是

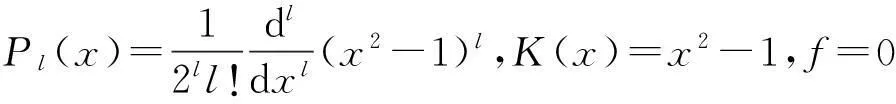
Hermite函数的微分形式是

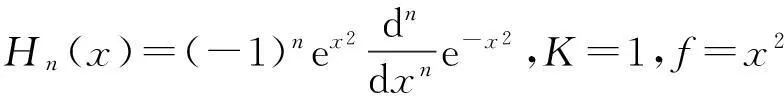
Laguerre函数的微分形式是

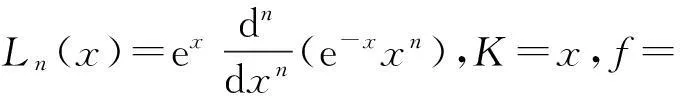
3个特殊函数形式上可以统一为

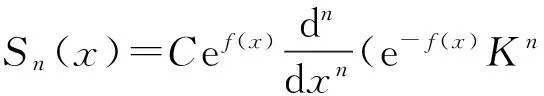
A(u)B(u+v)A(v)=B(v)A(u+v)B(u).

这是AB=BA的推广，是一类不可交换代数.类似三线性，有可能导致Pauli不相容原理(PEP)破缺[9-15]和非线性理论[11-13]等.这可以任意发展，发展到多个函数和任意组合等.这个方程已经用于共形场论、数学的结理论、辫子理论、算符理论、Hopf代数、量子群和二维流形的拓扑等.

3方程的不动点、定性分析及应用

对于不动点，y=f(x)方程经迭代(对应自相似分形)导致不动点方程x*=f(x*)，对应重整化群.f(x)是n次多项式，则有n个稳定或不稳定的不动点.对线性函数f=ax+b，x*=b/(1-a)是唯一解.若不动点具有周期性，则在一定条件下可以相应于极限环.这就联系于行星和天体轨道，甚至量子轨道及倍周期，包括来回跳跃的地震点[16-18]，周期性的经济现象等.

导数、斜率决定不动点的稳定性，联系于Lyapunov函数，相应于幻夸克和粒子的稳定性[11].进一步相应于非平衡态和生物等的稳定性.Lyapunov函数应用于非线性系统、非平衡态体系、耗散结构等可以确定产生稳定系统的条件.

方程的定性分析理论可以发展为：(1)三维、高维空间；(2)二阶、高阶方程，可以化为一阶，或对一阶求导后直接分析，或一个二阶及一个一阶等；(3)可以推广到方程组F(x,y,x′,y′)=0，G(x,y,x′,y′)=0，求出x′=f(x,y)，y′=g(x,y)等.

这可以发展为多维分析特征矩阵:

不解方程，变量周期变化时，对积分方程，最后要微分，解不变.对微分方程最后要积分，积分式中对微分项不变，对线性项有相同周期，对非线性项有不同周期.对线性代数方程周期相同，对非线性方程有所不同.

以速度v=dr/dt=P/m，加速度a=dv/dt=F/m为坐标轴的方法定性讨论，可以普遍应用于物理中，用v-a是纯运动学，P-F是动力学.一般简单方程为

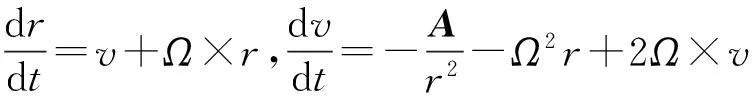
对各种非线性方程，如Henon映射、Lorenz模型、五维Navier-Stokes方程等作定性讨论，并阐明其物理意义.Lorenz模型中令y′=0，则y=rx-xz代入其余2式，类似Lotka-Volterra(LV)模型[19]，但z′=-cz+dxz；类似z′=0，则z=xy/b，方程组中仅有1项非线性.布鲁塞尔振子、Belousov-Zhabotinski(BZ)振荡[19]等都可以用定性方法及刘正荣的结果[20]等，其形象地描述极限环等变化.

保守系统对应鞍点、中心点，相应于不稳定态或单中心，具有单一性.耗散系统对应鞍点、焦点、结点，相应于演化过程或多种稳定态，具有多样性.

在环上是常数势，力、相互作用等某些量为0.因此极限环及其推广可用于导体内外、表面体内外等各方面，只要两方面分离，有所不同，如亚、超光速，粒子内外[1]等.

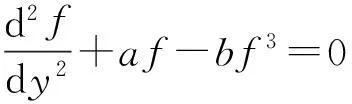
粒子或系统由一个方程或函数等描述，令它为f(x)，则对f(x)微分确定其稳定性.它应该是由拉氏量、能量确定，导数等于0就是粒子方程.

笔者将基于星云的旋转吸积盘的基本方程应用非线性方程的定性分析理论，得到双星形成的非线性动力学模型.将方程近似简化为只与速度相关的方程，则得到一个可解的简单模型，由此获得双星演化的非线性动力学机制.在一定条件下，二维空间中的一对奇点作为演化结果相应于双星.而在别的条件下，这些方程给出单个奇点，就相应于单星.因此，各种星的形成是星云演化的结果[22].这被Steinitz R等[23]在确定双星中自旋(旋转速度)间的相互关系时称为星云形成的双星张非线性模型.进一步，基于星云复杂的流体力学和磁流体动力学，从宇宙电动力学的Alfver方程出发，用非线性方程的定性分析理论讨论双星的形成也得到相同的结果，其中非线性相互作用和旋转取到非常关键的作用，而线性方程仅仅形成单星[24].这一模型不仅与著名的Boss等计算机模拟的结果是一致的，而且可以推广和发展.广义相对论是空间大尺度结构任何严格演化理论的基础.笔者计算了广义相对论中普适的2+1维平面的引力场方程，并基于这些方程讨论了星云的演化.对于不同条件，星云可以形成双星或单星，而任何简化的线性理论只能形成单星系统.这证明了非线性相互作用是非常普遍的，所以双星也是十分常见的[25].

用定性分析方法通常可以得到一些不等式和判别式.这些还可以结合相变、分岔-混沌理论和突变论[6]等，它包括由Lorenz方程及各种非线性方程等导致的判别式，这还可以联系于一般的结构稳定判别式.

更一般，方程等定性分析理论中的各种点、形对应于物理、天文、生物、社会等各种自然、社会科学中的某些现象.例如结点可以描述流体、正负电荷、相空间等.

如果结构对应于格点理论，那么定性方法可以推广到差分离散方程，此时仅微分变为差分.进一步，适用的方程推广到代数、积分等各种方程，推广到各种数学，或结合几何、代数、拓扑等中的方法.推广定性分析理论是汇、源及各类奇点、平衡点在微分、积分后性质不变.这对线性系统和非线性系统都成立.

4线性代数

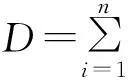
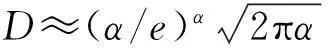
由α=n+d阶矩阵联系于分维矩阵、分维代数[26-27]，展开即α个变量、α个方程、α维空间，由此定义α阶行列式及α×β矩阵.α可以发展为负数、复数及其推广等[2-3].此外，行列式、矩阵可以发展为三维、高(n)维、分维、复数维及其推广等形式[2-3].

线性空间加和乘已经推广，如此线性相关或线性无关也可以推广.线性叠加原理、方程解、Fourier展开等各种与线性有关的都应该可以相应推广，起码在一定条件下.

进而线性代数应该发展为非线性代数，此时矩阵可以发展为高阶张量.对二元二次方程组，二次项系数是8个，是二维三阶张量.对二元r次方程组，相应系数是2r+1个；对n元r次非线性方程组系数是nr+1个，对应n维r+1阶张量.而一次项的方程组的系数是矩阵，零次项的系数是矢量.进一步确定这些张量间的关系.同时从直角坐标发展到曲线坐标，但对一般的二元二次方程组就解得四次方程，因此其发展可能是纯形式的.

任意非线性函数都可以展开化为Taylor幂级数.另一种非线性函数的展开是用Fourier级数.对一元函数用2组数ak,bk表示，然后先推广到二元m次的Fourier级数表示，再发展到方程组，这可能联系于非线性规划.

5数学物理量

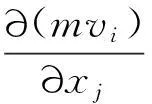
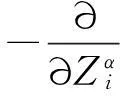
点乘决定流形度规，叉乘决定流形挠率；决定代数性质，这是代数用于几何.乘法不可对易是环、算符；加法不可对易的数学可以类比推广.在代数系统中乘法和加法都是运算，二者对称，其余还有扭量及其分维、复数维[11,26-27，29]等.

轻子(e,v)是最小质量态的扭量对，其实质是二维幺正群，联系于弱相互作用，e,v可以作为其二重态的积分表示.对应的计算散射振幅无紫外发散.三重态构成Weinberg-Salam理论，六重态形成大统一，可以推广为高秩、高维、弯曲空间.进一步，应该讨论协变微分和广义相对论中相应于量子力学的旋量场.

6数域的推广和复变函数的发展

量子力学数域(c数)的推广，即q数(算符、矩阵等).数学、物理中各种理论都可以相应推广，并再推广为任意的A(any)数.

量子力学用Pauli矩阵得到自旋及Pauli方程，推广到Dirac环就有相对论的Dirac方程及Kemmer方程[28]等.相对论用Pauli矩阵之一部分，因此组成Clifford数[28]，由此可以得到推广的Lorentz变换(GLT)[11,30-31].进而可以用全部Pauli矩阵，并推广到Dirac环.此外，数学上还可以再推广.

已知复变函数可导的条件是Cauchy-Riemann(C-R)方程：

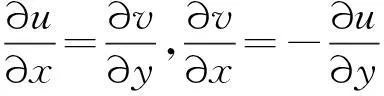
其中z=u+iv(一维).分析力学Hamilton形式的正则方程(1)统一为Poisson方程.刘正荣等[20]讨论的方程

完全类似力学中的Hamilton正则方程.对应电动力学中的无源电磁场方程

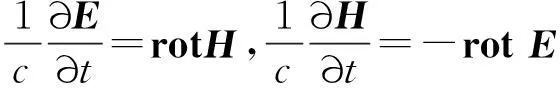
(H;iE)统一为Fik(三维)，它们的形式有某些类似.

一般说，复数、复变函数主要解决二维平面问题.这应该发展为三、四等直到n维的形式，对于四维可能联系于四元数(1,i,j,k).反之，推广到四元数、超复数等[25-26]时，复变函数都可以发展为相应的矩阵四元量函数、一般的矩阵函数等超复变函数，包括相应的三角函数，对应n维、分维、复数维[26,29，32]等.

各种数学及科学中实数、虚数统一的一个典型例子是相对论及相应的四维时空结构.超复变函数物理上可能联系于亚超光速、超对称及统一相对论和量子论等，可以用于所有数学、物理领域.

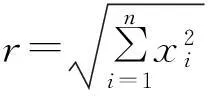
复变函数、复数系的普遍联系及相互类比、n维推广.更广泛地说，能用复变函数者都可以用二维复数系(1+i,1+j,1+k等)，它们彼此等价.整个量子力学的算符表示中，Heisenberg，Poisson，Schrodinger方程都必须乘以i，以保证厄米.理论上可以i→j,k，而宇称P,C=±1，可以由j,i平方统一.进而这些都可以推广到n维复数系.反之，用二维复数系者都可以用相应的复变函数代替，此时又对应矩阵函数.但超复数环有局限，相应的超复变函数也有局限.总之，复数发展为各种二维复数系，再发展为各种四元数系，并发展到n维及各种结合的复数系.复变函数也相应地进行各种推广.

参考文献：

[1] 张一方,刘正荣.粒子的相互作用、极限环和相变[J].数学物理学报，1999,19(4):424-431.

[2] 张一方.复数域的新推广及其物理意义[J].吉首大学学报：自然科学版，2008，29(5):31-34.

[3]CHANGYF.NewExtensionsofNumberSystemandComplexField,andTheirPhysicalMeaning[J].InternationalJournalofModernMathematicalSciences,2013,7(3):312-320.

[4] 张一方.数学分析的某些发展和新探索[J].吉首大学学报：自然科学版，2009，30(3):35-39.

[5] 张一方.数学中场论的某些新探索及其在物理学中的应用[J].吉首大学学报：自然科学版，2010，31(1):47-53;72.

[6] 勒内·托姆.突变论:思想和应用[M].周仲良，译.上海：上海译文出版社，1989.

[7]YANGCN.SomeExactResultsfortheMany-BodyProbleminOneDimensionwithRepulsiveDelta-FunctionInteraction[J].Phys.Rev.Lett.，1967,19(23):1 312-1 315.

[8]YANGCN.S Matrix for the One-DimensionalN-Body Problem with Repulsive or Attractive Delta-Function Interaction[J].Phys.Rev.，1968,168(5):1 920-1 923.

[9] CHANG Y F.Some Possible Tests of the Inapplicability of Pauli’s Exclusion Principle[J].Hadronic J.,1984,7(6):1 469-1 473.

[10] 张一方.在激光导致的高激发态原子中检验泡利不相容原理的适用性[J].自然杂志，1988,11(8):635-636.

[11] 张一方.粒子物理和相对论的新探索[M].昆明:云南科技出版社，1989.

[12] CHANG Y F.The Nonlinear Quantum Theory and Possible Violation of the Pauli Exclusion Principle[C]//AHN S H.Proc. of the 4th Asia-Pacific Phys. Conf.,V2.World Scientific，1991：1 483-1 486.

[13] CHANG Y F.Test of Pauli’s Exclusion Principle in Particle Physics,Astrophysics and Other Fields[J].Hadronic J.,1999,22(3):257-268.

[14] 张一方.各种可能的Pauli不相容原理的破缺和相应的统一(Ⅰ)[J].信阳师范学院学报，2010,23(3):360-365.

[15] 张一方.各种可能的Pauli不相容原理的破缺和相应的统一(Ⅱ)[J].信阳师范学院学报，2011,24(1):43-48.

[16] 张一方.地震的非线性动力学系统的探索[J].大自然探索，1997,16(3):51-55.

[17] 张一方.地震预报和某些新的理论探索[J].吉首大学学报：自然科学版，2010,31(2):48-54.

[18] CHANG Y F.Nonlinear Dynamics,Magnitude-Period figure and New Research on Earthquake[J].International Journal of Sciences，2012,11:1-9.

[19] 雷克L E.统计物理现代教程[M].黄畇，译.北京：北京大学出版社，1983.

[20] LIU Zhengrong,HU B,LI J.Global and Local Bifurcation in Perturbations of Non-Symmetry and Symmetry of Hamiltonian System[J].Int. J. Bifurcation & Chaos，1995,5(3):809-820.

[21] 栗弗席兹 E M,皮塔耶夫斯基 JT Л.统计物理学II(凝聚态理论)[M].王锡绂，译.北京：高等教育出版社，2008.

[22] CHANG Y F.A Nonlinear Dynamical Model of Formation of Binary Stars from a Nebula[J].Chinese Astron. Astrophys.(UK)，2000,24(3):269-274.

[23] STEINITZ R,FARBIASH N.Spectroscopically and Spatially Resolving the Components of Close Binary Stars[C].Dubrovnik,Croatia:ASP Conference Series,2003:20-24.

[24] CHANG Y F.Hydrodynamics and a Nonlinear Dynamical Formation Model on Binary Stars[J].Phys.Scr.，2007,76(4):385-387.

[25] CHANG Y F.Lorenz Model and Plane General Relativity Model on figuretion of Binary Stars[J].International Journal of Modern Theoretical Physics，2013,2(1):1-12.

[26] 张一方.数学,物理中分维的发展和分维时空理论[J].大自然探索，1991,10(2):49-54.

[27] CHANG Y F.Fractal Relativity,Generalized Noether’s Theorem and New Research on Space-Time[J].Galilean Electrodynamics,2010,21(6):112-116.

[28] 罗曼 P.基本粒子理论[M].蔡建华，译.上海：上海科学技术出版社，1966.

[29] 张一方.粒子的分形模型,复数维及其意义[J].大自然探索，1988,7(2):21-23.

[30] CHANG Y F.Imperfection of the Lorentz Transformation[J].Galilean Electrodynamics，2007,18(2):38-39.

[31] CHANG Y F.Extension and Complete Structure of the Special Relativity Included Superluminal and Nutrino-Photon with Mass[J].International Journal of Modern Theoretical Physics，2013,2(2):53-73.

[32] CHANG Y F.New Tree-Field Representations in Graph Theory,Extension of Dirac Extraction,Differential Test for Series of Positive Terms,Complex Dimension and Their Applications[J].Journal of Modern Mathematical Sciences,2014,9(1):1-12.

(责任编辑陈炳权)

Some Theories About Mathematical-Physical Equations and

Development of Complex Variables Functions

ZHANG Yifang

(Department of Physics,Yunnan University,Kunming 650091,China)

Abstract:First,the general equations and some of the simplified forms of their solutions are discussed.Next,the mathematical-physical equations and their symmetries are introduced.Thirdly,the fixed points,the qualitative analysis theory and corresponding applications on these equations are investigated.Fourthly,linear algebra is assorted from matrix.Fifthly,various quantities related with mathematics and physics are discussed.Finally,the extension of the number field and various super complex variables functions developed from the complex variables functions,etc.,are researched.

Key words:mathematical-physical method；equation；qualitative analysis；linear algebra；number field；complex variables functions

作者简介：张一方(1947—)，男，云南昆明人，云南大学物理系教授，主要从事理论物理研究.

基金项目：国家自然科学基金资助项目(11164033)

收稿日期：2014-10-12

中图分类号：O413.1

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.02.009

文章编号：1007-2985(2015)02-0038-08