钢铁企业烧结工艺蒸汽产量预测模型研究

（天津理工大学 天津市复杂控制理论与应用重点实验室，天津300384）

蒸汽作为钢铁企业能源体系中重要的组成部分，其生产需要许多的不可再生资源，例如煤炭、水、电等，为节约资源和提高生产效率，应对蒸汽产量做出合理的预测及决策，对企业的节能降耗有着重要意义。

由于烧结工艺运行过程中，存在变工况的情况，导致余热锅炉无法长时间稳定运行，使得蒸汽产量不稳定、波动大，所以很难建立基于机理的蒸汽产量模型。传统的经验调度方法难以及时做出相应的调整，导致蒸汽大量放散。因此，本文提出了基于逐步回归-小波神经网络预测方法。

神经网络是一种典型的数据驱动建模方法，对于输入、输出对象之间的非线性映射关系具有很强的匹配能力，在现实生产和生活中得到广泛的应用。其中，BP神经网络的应用是最为广泛的，但传统的BP算法除了存在收敛速度慢、容易陷入局部最优值外，泛化能力也一般。近年来提出的小波神经网络被实践证明在许多方面都优于BP神经网络，尤其在预测领域。文献[1]以理论结合实际的手段，对BP神经网络和小波神经网络的网络性能进行研究，研究表明小波神经网络更适合用于精度要求较高的预测。

逐步回归-小波神经网络预测方法，首先使用逐步回归对自变量进行筛选，优选对蒸汽产量影响较大的自变量集，简单省时、效率高；然后小波函数替代用来构造前向神经网络结构的Sigmiod传递函数，进而优化网络结构。小波函数具有在紧支撑中能任意逼近非线性连续函数，且在时频域都有分辨的特点，使得小波神经网络更适合学习局部非线性和快速变化的函数，这样结合不仅克服了神经网络容易陷入局部次优的缺点，也使得算法更易实现和应用。

逐步回归-小波神经网络模型在烧结工艺蒸汽产量预测中的应用是一种新的尝试，研究结果证明了该方法是行之有效的，且优于传统的BP神经网络和小波神经网络模型，有很好的实用意义和前景。

1 逐步回归

1.1 自变量选择对预测的影响

在实际生产中预测目标往往受许多因素影响，但影响程度有大有小，有些甚至微乎其微，所以自变量的选择对预测模型的建立有着重要的实际意义。在建立模型时，应尽量保留对因变量影响较大的重要因子，去除不必要的因子，从而得到最优自变量子集[2]。

1.2 逐步回归原理

逐步回归分析中，计算变量的偏回归平方和p值，选择p值最小的变量进行显著性检验，在给定显著性水平α下，若p≤α，则变量可以引入，并对引入的变量进行F检验；反之，将其剔除，并对其他变量进行检验，将p＞α的变量剔除，直至没有自变量能引入或剔除，最终得到最优的自变量子集。逐步回归分析的计算流程如图1所示。

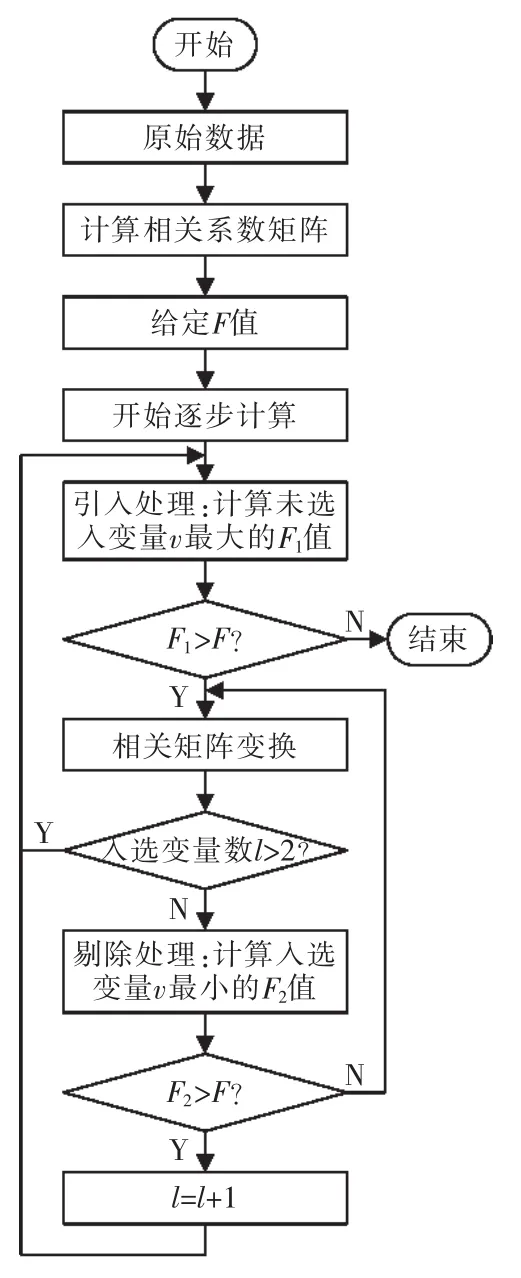
图1 逐步回归分析计算流程Fig.1 Calculation flow chart of stepwise regression analysis

2 小波神经网络

小波神经网络是基于小波变换而构成的神经网络模型。非线性小波基本函数替代用来构造前向神经网络结构的Sigmiod传递函数。该网络有效地结合了小波变换的时频局部特性和神经网络的自学习能力。小波网络是非线性回归结构，表示输入-输出之间的映射，其使用3层结构，且小波激活函数在隐层，其拓扑结构如图2所示。

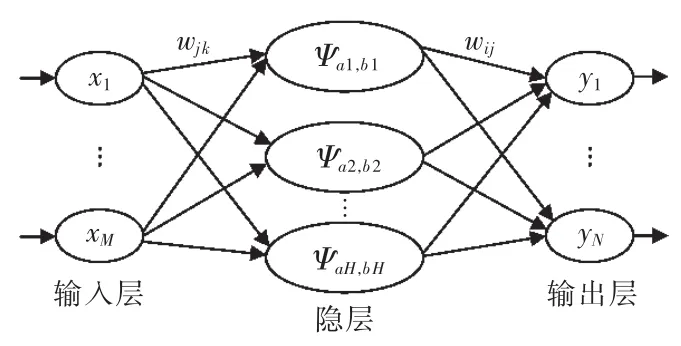
图2 小波神经网络的拓扑结构Fig.2 Topology of the wavelet neural network

图中，x1，x2，…，xM为小波神经网络的输入参数；Ψ（·）为母小波函数，aj和 bj（j=1，2，…，H）分别为伸缩因子和平移因子；y1，…，yN为小波神经网络的预测输出；wij和wjk为小波神经网络权值。

对于M为任意训练样本，H为隐层节点数，小波神经网络的输出经参数化后，表达式如下：

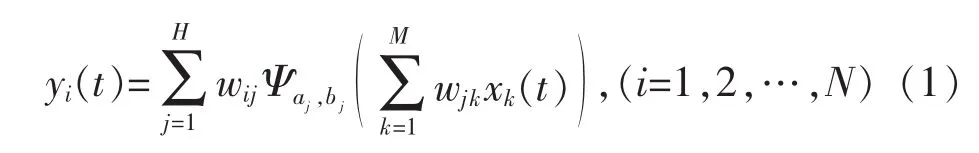
小波函数Ψ（x）的选择应满足框架条件：

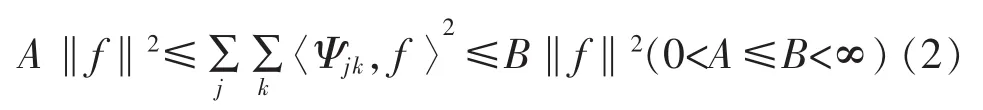
A，B分别为框架的上下界，即：

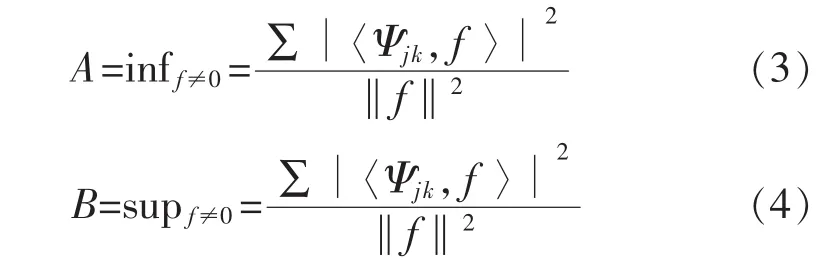
根据本文的需要，选择B/A≈1时的几乎紧框架的Morlet小波函数[3-4]：

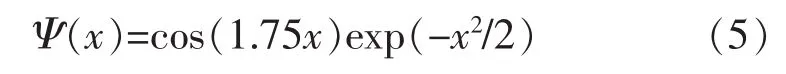
小波神经网络算法具体描述如图3所示。

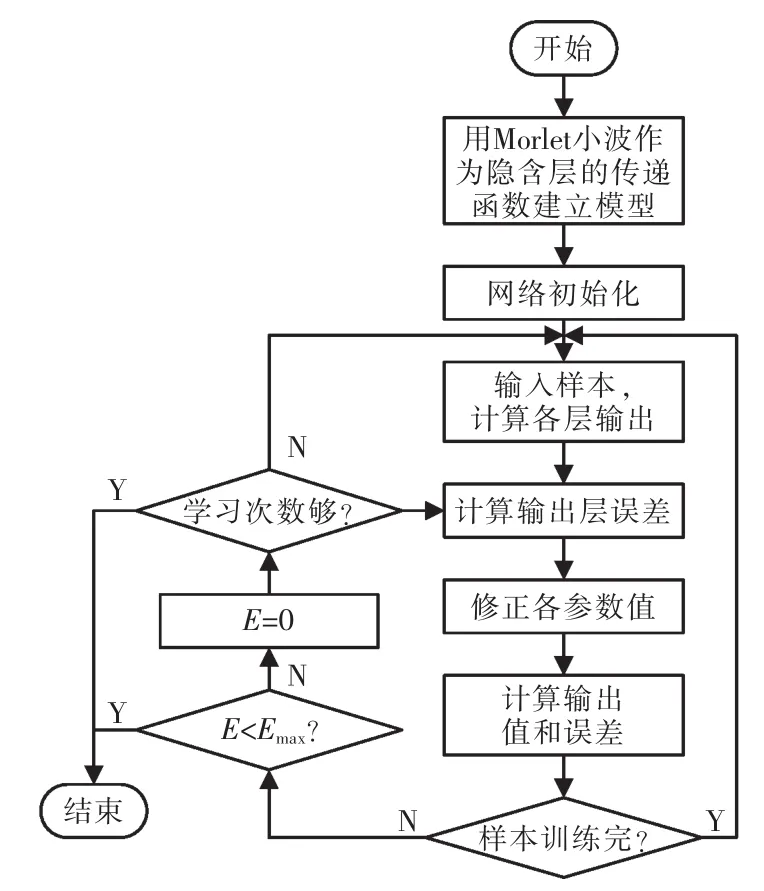
图3 小波神经网络算法流程Fig.3 Wavelet neural network algorithm flow chart

3 蒸汽产量预测模型

3.1 逐步回归选择最优自变量子集

选取20组数据用于通过逐步回归分析选择最优自变量子集，则样本组数n=20，影响烧结蒸汽发生量的主要因素有冷烧比、冷却风量、风压、风温、风速、料层厚度、烧结矿块度和冷却时间，则自变量个数为m=8。为避免去掉过多自变量，取显著性水平 α=0.05，Fin=2.95，Fout=2.91。

运用Matlab软件上的逐步回归指令stepwise来分析多变量情况下的最优模型问题，确定最优自变量子集中因子变量共有4个，分别为料层厚度、冷却风量、风速、风温。

通过逐步回归分析法，剔除了对预测目标影响较小的自变量，可以提高所建立的预测模型精度；而保留了影响较大的自变量，可以避免所建立模型预测的估计量有偏差，提高神经网络的泛化能力，确保预测精度；选择最优变量建立模型，减少了训练时间，提高了效率。

3.2 样本数据归一化处理

由于网络的输入、输出数据的量纲及数量级不同，而为了避免因为输入、输出数据数量级差别较大而造成网络预测误差较大，因此在网络预测前对数据进行数据归一化处理，把所有数据都转化为［0，1］之间的数[5]。

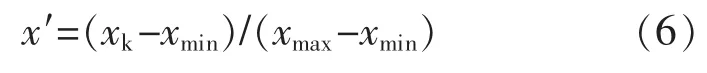
式中：x′为归一化数据；xk为输入或输出数据；xmin为数据序列中的最小值；xmax为序列中的最大值。

3.3 网络结构的确定

已知输入层节点数为4，输出层节点数为1，隐含层神经元的个数采用交叉验证法来确定，本文采用十折交叉验证法，验证间隔为6～12，得到最佳神经元个数为7，故此网络结构为4-7-1。

3.4 预测结果分析

本文以某钢铁企业烧结厂为例，选取2011年7月份的数据进行仿真，共选用200组数据，训练样本集为前160组，测试样本集为后40组，其中使用20组数据来进行逐步回归分析，选定最优自变量子集。

采用传统BP神经网络、小波神经网络和逐步回归-小波神经网络预测方法得到的预测结果如图4所示。3种预测模型的复相关系数分别为0.907、0.988、0.993，残差平 方 和 分 别为 71.577、37.041、15.240。由图4可以看出，不但可以利用BP神经网络和小波神经网络建立烧结蒸汽产量的预测模型，且结合逐步回归和小波分析的BP神经网络蒸汽模型的精度和准确度均得以提高。

为了进一步验证本文所提方法的有效性，选取均方根误差（NRMSE）和平均绝对百分比误差（MAPE）作为判断预测效果的依据，计算公式如下[6]：

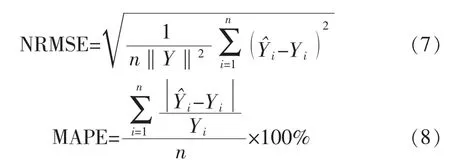
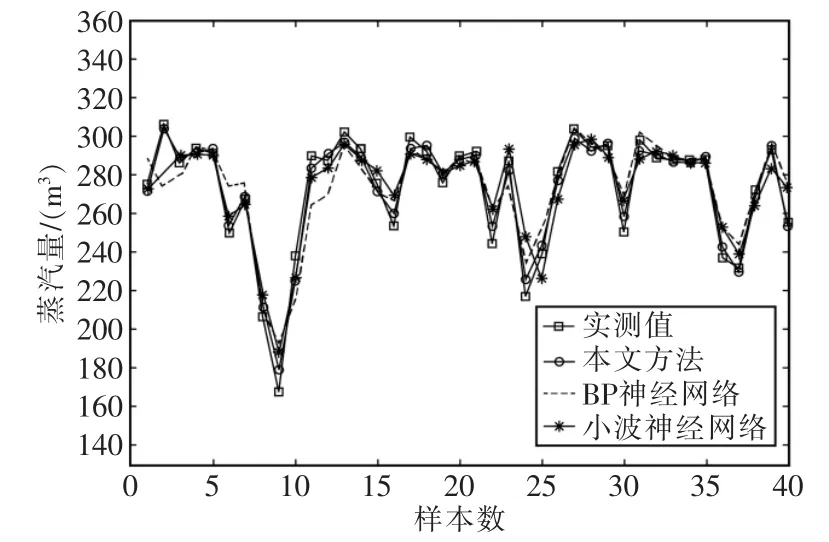
图4 预测曲线比较Fig.4 Prediction graph

各方法预测精度如表1所示。

表1 预测结果比较Tab.1 Comparison of prediction results

通过分析可知，逐步回归-小波神经网络的预测能力与小波神经网络相差不大，但在程序运行过程中表明逐步回归-小波神经网络的训练速度要远远快于小波神经网络。这是由于逐步回归法对自变量筛选的作用，选用最优子集进行预测，避免了预测模型的估计量有偏差，改进了小波神经网络对个别点的拟合存在一定偏差的缺点。

4 结语

综上所述，逐步回归方法能够根据研究需要达到的精度，筛选出对蒸汽产量有显著影响的因素，简化网络的拓扑结构，以提高网络的泛化能力，其性能要优于单纯使用小波神经网络。但在数据波动较大处，仍存在着一定的误差，因此，在接下来的研究中，需要综合考虑更多因素，改进建模方法，使模型更加符合实际情况。

[1]冯再勇.小波神经网络与BP网络的比较研究及应用[D].成都：成都理工大学，2007.

[2]戚丹，包腾飞，康业渊，等.基于逐步回归-BP神经网络的大坝变形监测模型[J].水电能源科学，2013，31（8）：110-111.

[3]孙延奎.小波分析及其应用[M].北京：机械工业出版社，2005.

[4]Harold S，Brian A，Shubha L，et al.Neural network adaptive wavelets for signal representation and classification[J].Optical Engineering，1992，31（9）：1907-1916.

[5]冯艳，付强，李国良，等.水稻需求量预测的小波BP网络模型[J].农业工程学报，2007，23（4）：66-69.

[6]杜雷.贝叶斯神经网络在蒸汽压力预测中的应用[D].大连：大连理工大学，2011.