一种新的火电机组主汽温智能控制方法研究

辛晓钢 ，陈世慧，王 彪，方彦军，唐若笠

（1.内蒙古电力科学研究院，呼和浩特 010020；2.武汉大学 自动化系，武汉 430072）

内蒙古地区风电装机容量大，火电机组调峰任务繁重[1-2]。主汽温控制是火电机组调峰的重要环节，关系着机组能否较好地应对外界扰动，保证安全、平稳运行[3]。在火电机组的实际运行过程中，对于喷水减温扰动下的主蒸汽温度控制，发电企业常采用具有前馈补偿的串级PID控制策略[4]，但对于内蒙地区频繁快速升降负荷的实际情况，往往达不到理想的控制效果。

针对这一问题，国内外学者展开了大量的研究与实验工作，目的在于改善火电机组主汽温控制系统在受到外界扰动时的动、静态品质。文献[5]采用模糊自整定的方法设计PID控制，并应用于主汽温控制，获得了较小的超调量和调节时间；文献[6]采用免疫遗传算法与BP神经网络相结合，并应用于主汽温PID控制系统，取得了良好的控制效果；此外，一些先进的控制器[7]及先进的控制结构[8]也都被引入火电厂热工控制过程。

为进一步实现先进控制技术与人工智能算法在火电机组主汽温控制系统中的应用，改善机组控制品质，本文提出了一种基于仿人智能粒子群的广义预测PID控制策略，应用于火电机组主汽温控制，并通过仿真实验验证了所提算法及控制策略的有效性。

1 仿人智能粒子群算法

1.1 基本粒子群优化算法

粒子群算法 PSO（particle swarm optimization）由Kennedy和Eberhart于1995年正式提出，由于其应用普遍，本文不再赘述，具体公式表示如下：

种群中的粒子在初始化后按照上述公式进行迭代，当到达给定迭代次数或满足某个预设的寻优精度后，最后一次迭代产生粒子群的群体最优位置及其所对应的适应度函数值，即为粒子群算法所寻得的最优解。

1.2 仿人智能粒子群算法

本文从仿生学角度出发，提出了一种新的仿人智能粒子群算法HSI-PSO（human simulated intelligent PSO）。首先，仿照人脑的学习和记忆特性，将粒子迭代过程中每一代所形成的“认知”进行积累，并按照指数衰减的形式引入粒子速度更新公式：一方面，有助于粒子通过历史“认知”更好地进行全局寻优；另一方面，由式（1）可知，对于基本粒子群算法，当粒子陷入局部最优，当前代的“认知”近似为零（近似等于0），粒子难以跳出局部最优，算法早熟；而引入历史“认知”后，此时不为0的历史“认知”会将粒子拉离该局部最优值，进而防止算法出现“早熟”。HIS-PSO算法的速度更新公式如式（3）所示：

式中：ξi为截止第t次迭代，算法每一代的认知有效因子，该参数用于指定不同阶段认知对当前决策的影响权重，本文称之为“记忆因子”。如式（4）所示，该参数按照指数方式进行衰减，且在任何时刻，所有ξi之和应为1。

此外，为进一步增强算法的全局优化能力，为每个粒子引入邻域搜索行为，按式（1）及式（2）更新位置前首先进行判断，如果目标位置的适应度函数值较当前位置更优，则更新；反之，则开始邻域搜索行为，即在步长（Step）范围内随机搜索目标位置，若较当前位置更优，则更新，否则重新搜索；若达到最大搜索次数（Try_number）后还未找到更优位置，则在步长范围内随机跳动。

1.3 数值仿真实验

为验证所提HIS-PSO算法的有效性，选取如表1所示的测试函数进行仿真分析，并与标准粒子群算法PSO、带扩展记忆的粒子群算法PSOEM[9]、加强学习与联想记忆粒子群算法SLAM-PSO[10]、人工鱼群算法AFSA[11]、粒子群优化鱼群算法PSO-FSA[12]等主流优化算法进行对比分析。

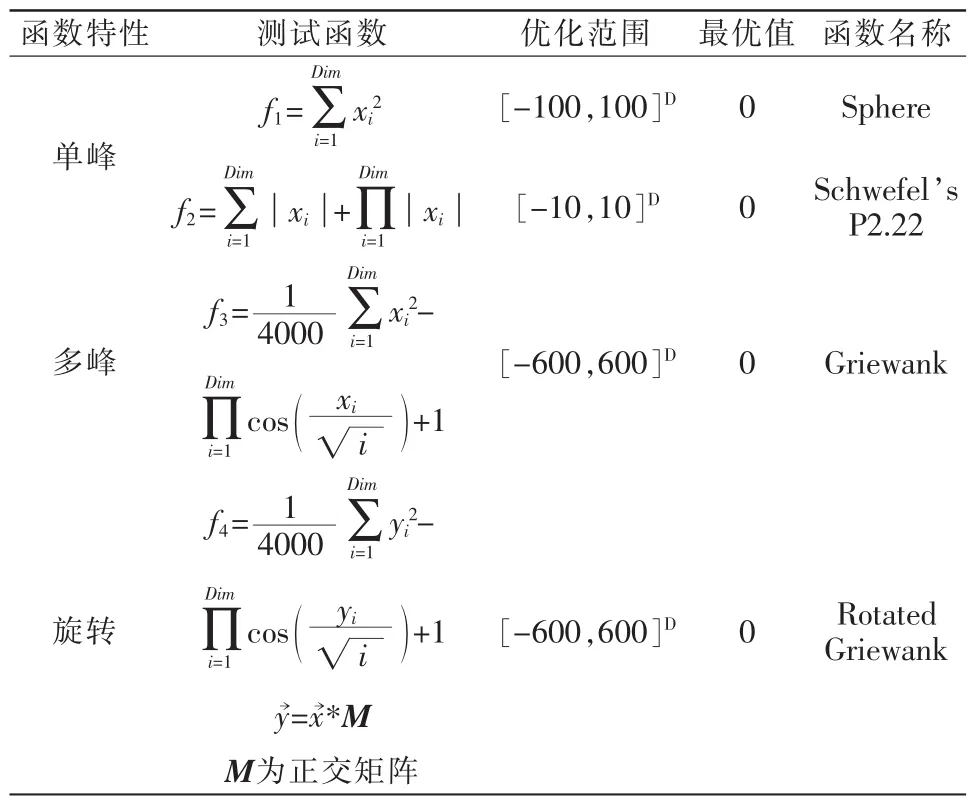
表1 基准测试函数Tab.1 Basic test functions

仿真环境为Matlab R2007b，各算法参数设置如表2所示，测试函数维数设为30维，种群规模50个，最大迭代次数5000代，各算法独立运行50次，实验结果如图1所示。

表2 各算法参数设置Tab.2 Parameters setting of the algorithms

图1 各算法平均进化曲线Fig.1 Average evolution curves of the algorithms

由仿真结果可见，对于表1所列目标函数的优化问题，本文所提出的HSI-PSO算法较标准粒子群算法PSO、改进型粒子群算法PSOEM、SLAM-PSO、以对多维多极值函数具有较强优化能力著称的人工鱼群算法AFSA及其改进型算法PSO-FSA而言，具有更快的收敛速度和更高的寻优精度。尤其当目标函数具有多峰值或Rotated特性后，PSO、PSOEM等算法易出现早熟现象，而HSI-PSO算法则能够跳出局部最优，具有更强的全局优化能力。

2 基于广义预测PID的参数优化模型

智能优化算法应用于主汽温PID控制系统，首先需要建立合理的参数性能评价指标，使智能算法能够相对实时且较为准确地计算出每组PID参数对应的控制效果。

广义预测控制GPC（generalized predictive control）能够有效克服系统滞后特性，且具有鲁棒性强、在线计算方便等特点。本文通过GPC方法定义智能优化算法下的PID参数性能指标，实现HIS-PSO算法与主汽温PID控制系统的关联。

2.1 广义预测PID控制器

常用的增量形式PID控制表述如式（5）所示：

记 ω0＝KP+KI+KD，ω1＝-KP-2KD，ω2＝2KD则式（5）可以改写为

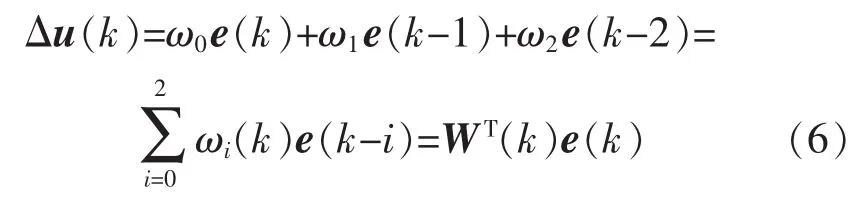
将式 （6）带入广义预测控制中的CARIMA模型，可得：

为了预测超前j步输出，通过Diophantine方程可得未来j步输出：

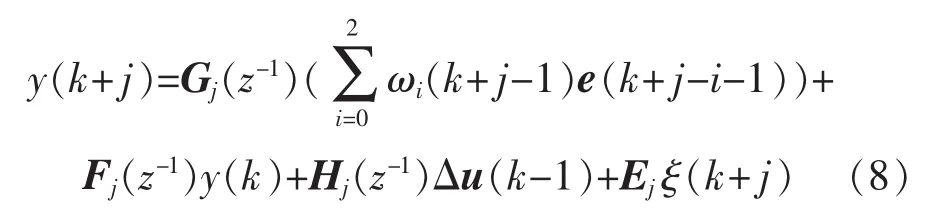
式中，Ejξ（k+j）为未来噪声。

广义预测控制中，t时刻的性能指标通常采用如下形式：

最优控制率为

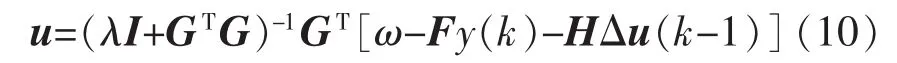
将式（8）带入式（9）可得：

式中：N=N2-N1为预测时间；Lj＝ω （k+j）-HjΔu·（k-1）-Fjy（k）。

由最优控制率式（10）可得其增量形式为

通过最小化广义预测性能指标，可推得整个时域的控制变量为

则最优控制序列为

系统只取当前时刻的控制变量Δu（k），通过式（11）即可计算得到当前优化的控制器参数 ω1（k），ω2（k）和ω3（k），进而可以计算得到最优PID参数为

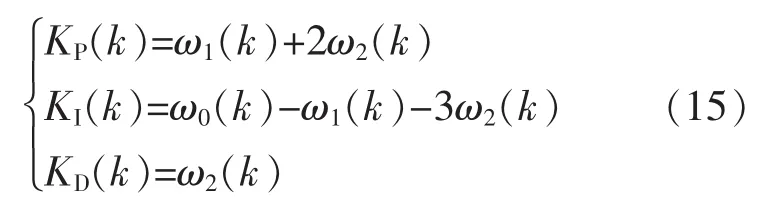
2.2 PID参数优化模型

由于主汽温PID控制系统的串级结构，根据PID参数优化问题公式推导，分别构建主、副回路的PID 参数优化模型如式（15）、式（16）所示：

式中：下标1表示主回路参数；下标2表示副回路参数；J为对应回路的广义预测优化指标；为主回路 PID 参数；为副回路PID参数；S为对应的参数取值范围。

3 基于HIS-PSO优化广义预测PID的主汽温控制仿真分析

本节采用文章第一节所提出的具有较强全局优化能力的HIS-PSO算法对主汽温串级PID控制系统进行优化，适应度函数分别取式（16）及式（17）所示的性能指标函数，在Matlab 2007b/Simulink仿真平台下搭建仿真系统。

3.1 主汽温串级系统对象模型

主汽温对象具有大延迟、大惯性和时变性等特点，主要表现为过热器管道较长且蒸汽容积较大，减温水流量变化到过热器出口蒸汽温度变化具有较大的延迟；当机组升降负荷时，主汽温的动态特性也会发生显著变化。火电厂主汽温常采用串级PID进行控制，由喷水减温器出口向副回路控制器引入反馈信号，具体结构如图2所示。对于超超临界锅炉，70%负荷（700 MW）下主汽温常用模型如表3所示，本文基于此模型验证所提控制策略的有效性。

图2 主汽温串级控制系统结构Fig.2 Structure of main steam temperature cascade control system

表3 70%负荷下主汽温对象模型Tab.3 Model of main steam temperature under 70%load

3.2 仿真实验与结果分析

在70%负荷下，采用表3所示对象模型，测试系统在本文所提控制策略下的阶跃响应（幅值605℃），此外，与标准粒子群算法以及工程常用的Z-N整定方法结果进行对比。其中，PSO与HIS-PSO算法种群规模均设为50，迭代次数为100代，主副回路PID参数优化范围及控制量约束范围如表4所示。

表4 PID参数优化范围及控制量约束范围Tab.4 Range of PID parameters and controlled variables

分别采用HIS-PSO、PSO和Z-N 3种方法进行串级PID参数整定，结果如表5所示，基于表5结果的主汽温控制系统阶跃响应如图3所示。

表5 各方法PID参数整定结果Tab.5 Results of different PID tuning methods

图3 各方法下的主汽温阶跃响应Fig.3 Step response of main steam temperature

由仿真结果可见，基于HIS-PSO的广义预测PID能够实现对大延迟、大惯性的主汽温度的有效控制，相比于PSO优化PID方法以及常规的Z-N整定PID方法，本文所提算法具有更小的超调量和更短的调节时间，控制效果显著优于另外2种控制方法。

4 结语

本文针对内蒙地区火电机组调峰压力大，主汽温扰动频繁进而难以控制等问题，首先提出了一种仿人智能粒子群HIS-PSO算法，并通过数据实验证明该算法较几种主流粒子群优化算法具有更强的全局优化能力。在此基础上，结合广义预测控制思想，提出了一种基于HIS-PSO算法的主汽温广义预测PID控制策略，仿真实验表明，该方法较粒子群优化PID，Z-N整定PID等常规控制手段具有更好的控制效果，对于频繁扰动下的主汽温控制具有较强的实用性。

[1]王小海，齐军，候佑华，等.内蒙古电网大规模风电并网运行分析和发展思路[J].电力系统自动化，2011，35（22）：90-96.

[2]赵桂廷，李强，丛雨，等.内蒙古电网大规模风电消纳问题分析研究[J].内蒙古电力技术，2013，31（2）：1-4.

[3]Chaibakhsh，Ghaffari A，Moosavian S.A simulated model for a once-through boiler by parameter adjustment based on genetic algorithms[J].Simulation Modeling Practice and Theory，2007（15）：1029-1051.

[4]Zhu Qian，Zhang Jingqiao，Wang Jian.Design of fuzzy and CMAC parallel controller based on GA for main steam pressure in supercharged boiler[C]//Control and Decision Conference，2008：4934-4938.

[5]武彬，张栾英.模糊自整定PID控制在主汽温控制中的应用[J].计算机仿真，2015，32（2）：387-390.

[6]Han Li，ZhangZhenyu.Theapplication ofimmune genetic algorithm in main steam temperature of PID control of BP network[J].Physics Procedia，2012（24）：80-86.

[7]冯晓露，覃来丰，岑可法，等.基于遗传算法的模糊控制器动态优化方法[J].浙江大学学报：工学版，2007，41（3）：95-99.

[8]田沛，宿喜峰，马平，等.基于自抗扰技术的主汽温全程控制[J].中国电机工程学报，2006，26（15）：73-77.

[9]段其昌，黄大伟，雷蕾，等.带扩展记忆的粒子群优化算法仿真分析[J].控制与决策，2011，26（7）：129-132.

[10]段其昌，张广峰，黄大伟，等.加强学习与联想记忆的粒子群优化算法[J].计算机应用，2012，32（12）：58-61.

[11]李晓磊.一种新型的智能优化方法-人工鱼群算法[D].杭州：浙江大学，2003.

[12]段其昌，唐若笠，徐宏英，等.粒子群优化鱼群算法仿真分析[J].控制与决策，2013，28（9）：159-163.