遗传算法优化神经网络的直线电机定位力辨识

（哈尔滨工业大学 航天学院，哈尔滨 150001）

电机作为一种执行元件，被广泛应用于生产、生活的各个领域。直线电机更是凭借其相对于传统伺服系统的高效率、高精度等优势普遍应用于高精度运动控制系统之中。然而，电机在运转的过程中常常受到各种扰动的影响。除了电流波纹等外界扰动之外，永磁电机由于自身机械结构和设计的局限性，难免存在磁拉力波动、齿槽力波动和边端效应等自身扰动。在生产生活中为了实现较好的伺服控制，特别是在高精度伺服系统中，必须对这些扰动进行辨识，以进行补偿而获得更好的控制效果。以上这些波动、扰动在永磁直线电机中通常只与电机初级与次级之间的相对位置有关，统称为直线电机的定位力。考虑到定位力辨识的必要性，文献[1]中采用递推最小二乘法对直线电机的定位力进行了辨识。该方法采用改进的最小二乘法，虽然一定程度上弥补了最小二乘法计算量大、实际应用性差的缺陷，但仍为一种参数化的辨识方法，其辨识精度对模型的精确程度依懒性很高，由于理论模型不能精确描述实际系统，抑或考虑到计算复杂度等方面的问题而采用简化的数学模型，使得辨识结果存在较大误差；文献[2]采用了齿槽推力波动标定方法和线性插值计算方法对齿槽推力进行了建模辨识。该方法对齿槽力采样、标定，相比之下，标定虽然方法比较简单易懂，但操作工程量较大，而且辨识精度对插值方法依懒性比较大，如果采用插值方法不当，可能会因此造成在标定点之间的较大误差，因而在实际应用中会有一定的局限性。考虑到以上问题与局限性，以某光刻机项目中的直线电机为例，本文提出了一种基于遗传算法优化神经网络的直线电机定位力辨识方法。该方法利用人工神经网络特有的表达任意非线性映射的能力，对非线性的直线电机定位力进行辨识，并通过遗传算法对人工神经网络进行优化，提高算法收敛速度及辨识精度。

1 直线电机定位力特性

直线电机定位力主要是由电机齿槽力波动与边端效应形成的，通常只与直线电机的初级和次级位置相关，因而直线电机定位力可视为一个关于直线电机位置的非线性函数。直线电机齿槽力是由直线电机定子磁场和动子铁芯相互作用形成，齿槽力吸引动子向附近某个磁拉力平衡点移动；边端效应是由于直线电机的开槽和动子的长度有限，磁钢端部与电枢铁心端部作用导致[1]。理论上，可得到直线电机的齿槽力矩波动和边端效应的数学表达式为

式中：τ为极距；Lg为气隙长度；Lm为磁钢厚度；Br为径向磁密；Lk为铁芯长度；Δ＝Lk+iτ表示动子铁芯横跨的极距；p为直线电机极对数；μ0为磁导率；x为距离轴线的距离。由直线电机的定位力数学表达式可以得到，直线电机的定位力是一个与直线电机位置有关的非线性函数，而且具有一定周期性。然而，数学表达式仅仅在理论分析过程中有较好的作用，在实际应用过程中，由于电机制作、装配等原因导致的电机参数各处不同且与理论计算有一定差距，因而需要使用合适的方法对直线电机的定位力进行辨识。

2 神经网络及遗传算法原理

2.1 人工神经网络

人工神经网络是依据仿生学的原理，模拟人脑神经系统的工作方式，使机器具有类似于神经网络一样的感知、推理和学习能力，进而用来处理一些比较复杂的问题。神经网络的实质是一个非线性系统，通过各权值与阈值之间的相互关系及各节点输入输出的局部非线性来实现整个网络模型的非线性映射关系。神经网络的应用通常具有以下显著特点：具有很强的自适应和自组织能力，通过学习和训练来逼近非线性映射关系；信息处理并行化，实现并行处理信息的方式，提高运算的效率。在众多人工神经网络的类型中，BP神经网络应用最为广泛。BP神经网络是一种多层前馈神经网络，如图1所示，其主要特点是信号向前传递，误差反向传递。信号前向传递过程中，输入信号经隐含层处理输出，每一层神经元影响下一层神经元状态，如果输出层得不到期望输出则反向传播，改变阈值和权值，使得神经网络不断逼近期望输出，从而使整个网络逼近所需的非线性映射关系。

图1 BP神经网络拓扑结构Fig.1 BP neural network topology structure diagram

BP神经网络学习和训练过程如图2所示，首先进行网络的初始化，包括输入层、隐含层与输出层节点数的确定和网络各权值与阈值初值的初始化等。其次需要按照式（5）、（6）分别对隐含层与输出层的输出进行计算。

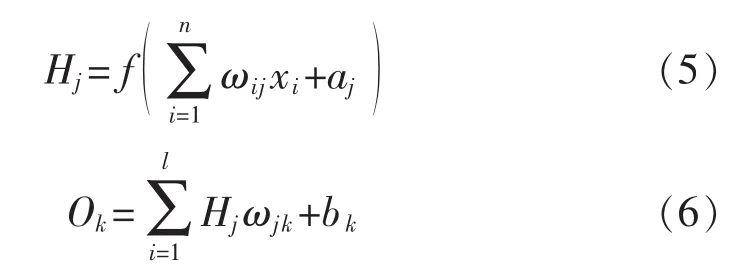
式中：Hj为第j个隐含层节点输出；Ok为第k个输出层节点输出；ωij、ωjk分别为输入层与隐含层和输出层之间的权值；a、b则分别为隐含层与输出层的阈值。

最后按式（7）和式（8）由误差e对各权值和阈值进行更新：

式中，η为学习率。

图2 BP神经网络算法流程Fig.2 BP neural network algorithm flow chart

2.2 遗传算法

遗传算法是基于自然界遗传机制和生物进化论而形成的一种并行随机搜索最优化方法。其模拟生物界中自然选择和群体遗传机制，采用简单的编码技术来表示各种复杂的结构，并通过一组编码表示和进行简单的遗传操作以及优胜劣汰的自然选择来指导学习和确定搜索的方向[3]。对于一个确定的种群，遗传算法大致通过以下几个过程实现：

选择遗传算法的选择操作有多种方法，大致可归纳为轮盘赌法、随机联赛选择法等23种方法[4]。遗传算法通过适应度选择优质个体而抛弃劣质个体，体现了“适者生存”的原理[5]。

变异遗传算法依据算法中设定的变异率对已经进行编码的个体随机选择基因进行改变，以产生新的个体，进而提高局部搜索能力。

交叉遗传算法对应于个体的编码形式采用适合的交叉方法交换个体间的基因，从而实现个体的进化。

遗传算法的算法流程如图3所示。

图3 遗传算法流程Fig.3 Genetic algorithm flow chart

3 直线电机定位力辨识

3.1 辨识方法

BP神经网络使用广泛，算法已经十分成熟，因而在辨识中采用BP神经网络为辨识模型主体。BP神经网络虽然可以完成对所需的非线性映射的逼近，但是其计算效率和结果均具有可以进一步优化的余地。均衡考虑计算复杂度与结果精度，使用遗传算法对神经网络进行优化。遗传算法优化BP神经网络的本质是通过遗传算法获得更好的神经网络初始权值及阈值，即用个体代表网络的初始权值和阈值，将预测误差作为个体的适应度函数，通过变异、交叉和选择等操作收敛得到最优个体，从而实现对BP神经网络的优化。具体算法如图4所示。

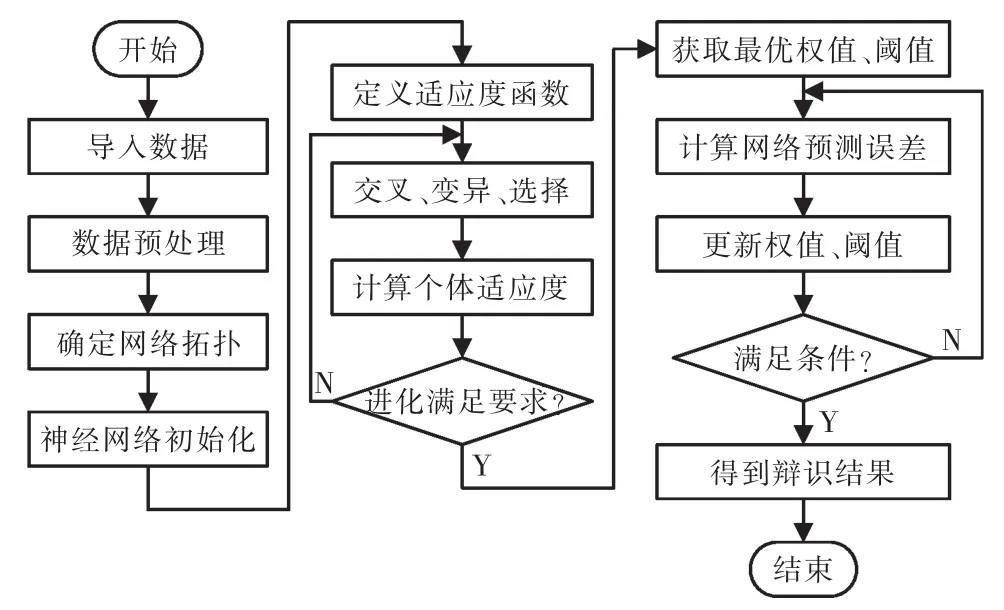
图4 遗传算法优化BP神经网络辨识流程Fig.4 Identification flow chart of BP neural network optimized by GA

3.2 辨识实验配置与结果

被辨识的目标直线电机在水平与垂直方向均采用气浮支撑，该机械结构使得机械摩擦等具有近零特性，可尽可能减小机械摩擦阻力的影响；动子位移数据采用分辨率为50 nm的增量式光栅尺进行采集，整个系统采样频率为5000 Hz。由电机的动力学方程可得，除了近零机械摩擦力，还需尽可能降低运动的粘滞摩擦力和电机磁阻推力。考虑到运动的粘滞摩擦力正比于速度、磁阻推力正比于绕组电流，直线电机在低匀速状态下可将二者影响降至最低，因而令直线电机以0.01 m/s匀速运动，利用加速度计得到加速度曲线，进而得到电机定位力波动曲线，其中加速度曲线如图5所示。

图5 加速度曲线Fig.5 Diagram of acceleration curve

在所得10000组数据中选择8000组数据用于遗传算法优化神经网络对定位力波动进行辨识，并利用2000组数据验证辨识模型的可行性。辨识结果如图6所示。

由仿真得到定位力波动辨识均方误差为0.224802，结合图6可以得到遗传算法优化神经网络比较精确地对定位力进行了辨识。

图6 定位力辨识结果Fig.6 Identification result of cogging force

4 结语

针对工程中需要解决的直线电机定位力波动问题，本文给出了一种基于遗传算法优化神经网络的辨识方法。理论分析及实验表明该方法具有自适应性、应用局限小等优点，并且该方法在实际工程辨识的过程中具有可行性，具有良好的应用价值。

[1]陈兴林，杨天博，刘杨.直线电机定位力波动的辨识及迭代补偿方法[J].电机与控制学报，2015，19（2）：60-65.

[2]穆海华，周云飞，温新，等.直线电机齿槽推力波动的标定与补偿方法[J].电机与控制学报，2009，13（5）：721-727.

[3]徐磊.基于遗传算法的多目标优化问题的研究与应用[D].长沙：中南大学，2007.

[4]Potts J C，Giddens T D，Yadav S B.The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J].Systems Man& Cybernetics IEEE Transactions on，1994，24（1）：7-86.

[5]葛继科，邱玉辉，吴春明，等.遗传算法研究综述[J].计算机应用研究，2008，25（10）：2911-2916.

[6]王小川，史峰，郁磊，等.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013.