风电机组运行稳定性研究

（河北工业大学 控制科学与工程学院，天津 300131）

近年来，人类社会的快速发展使人们的能源需求逐步增加。风能作为可再生能源开发的典型代表，受到了世界各国的关注[1-3]。风力发电受到越来越多的关注，对与风力机相关的控制技术的研究也取得了一定进展。国内外众多学者针对风机控制问题进行了大量研究[4-6]。文献[7]在传统风能追踪控制策略的基础上，提出通过改变最优增益系数来追踪最佳风能利用系数的自适应转矩控制策略。文献[8]应用基于BP算法的神经网络控制策略对风力机桨距角进行控制，达到了既能满足电网电能质量要求又能实现最大功率跟踪的目的。文献[9]提出了高阶滑模控制策略，可以在2种工作域下确保系统稳定并具有较好的鲁棒性。文献[10]采用基于单神经元自适应PID的异步变桨控制策略或多变量控制策略设计控制器，减少风轮转矩的波动和桨叶的不平衡载荷。尽管这些控制方法效果良好，但前提是基于精确的数学模型，而风力发电系统作为一个复杂的非线性系统，数学模型不能精确建立，难以将这些方法运用到实际的工程中[11]。

按照风速点划分，变速变桨风力发电机组一般分为3个运行区域[11-13]，区域一是风速达到切入风速之前，发电机不工作，风轮做机械转动，属于风机启动阶段；区域二是风速达到切入风速后，通过控制发电机转矩达到输出功率最大化；区域三是风速达到额定风速，通过控制桨距角将风机输出功率稳定在额定功率。本文对区域二进行研究，通过状态反馈控制设计了控制器，并计算出了在该控制器下风机运行的稳定域。最后通过仿真验证了在风速低于额定风速时，该控制器能达到使风轮转速达到期望转速的控制目标，且当风轮转速在稳定域内运行时，该控制器可使系统稳定。

1 模型描述

由空气动力学可知，风力机是用来捕获风能，将风能转换为机械转矩的关键部件，那么风力机从风能中吸收的机械功率[14-15]为

式中：ρ为空气密度；R为风轮半径；v为风速；Cp为风能利用系数，是一个关于叶尖速比λ和桨距角β的函数，表示风能转换为机械能的转换效率。其中叶尖速比定义为

式中，ωr为风轮转速。

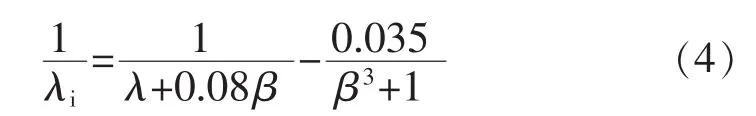
风电机组叶尖速比与功率系数的对应关系曲线如图1所示。

图1 叶尖速比与功率系数关系Fig.1 Tip speed ratio and power coefficient relationship

本文中风机工作在固定桨距角β＝0°，从图1中可以看出，在叶尖速比λopt=8.1时，得到最大风能利用系数Cpmax=0.48。因此，最优风机的角速度为

风速的任何变化都会引起叶尖速比的改变，发电机产生的功率随之变化。用气动转矩表示功率为

式中，Ta为气动转矩。由文献[16]得出：

式中，θr为转子转动角度；ωr为风轮转动角速度；Jr为总的机械惯性；Kt和B分别为粘滞摩擦系数和刚度系数；Ta为气动转矩；μ为利用系数；Te为发电机电磁转矩；τ＝0.01。

为简化模型，可通过近似计算得：

风力发电机组变桨控制方案如图2所示。

图2 风力机变桨控制方案Fig.2 Wind turbine pitch control program

2 控制器设计

2.1 问题描述

风力发电机组数学模型表达形式为

2.2 状态反馈

首先通过状态转换，将原问题转换成系统在原点稳定的问题。

整理得：

式中：

设计控制器：

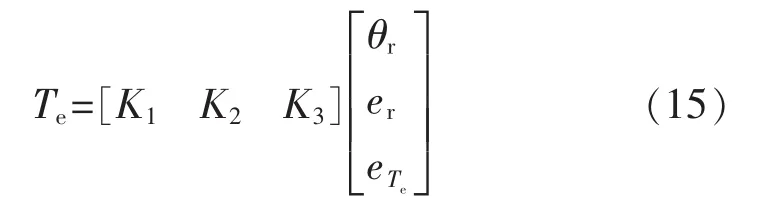
进而：

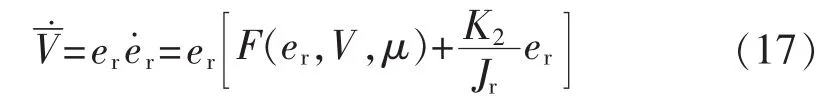
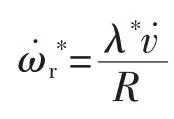
2.3 稳定性证明

将 K1＝-B 和 K3＝-Jr代入式（16）中，得：

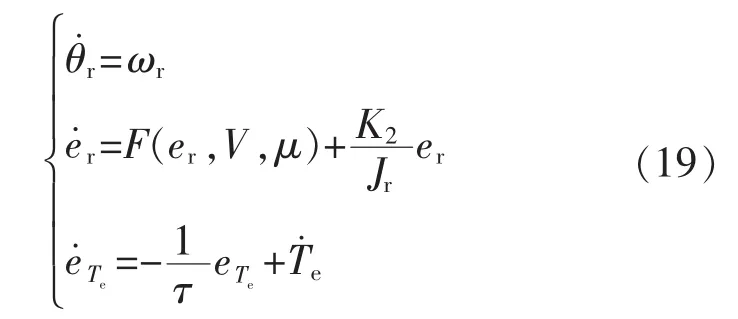
2.4 稳定域分析

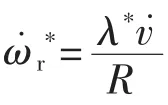
故在该控制器下的风力发电机组运行的稳定域为0≤ωr＜5，在此范围内，风力发电机组可正常运行。

3 数值仿真

本文采用Simulink搭建了风力发电机组仿真平台，对系统进行仿真。在风速低于额定风速的情况下，首先对设计的状态反馈控制器的仿真结果进行了分析，再对计算的稳定域进行了验证和分析。已知风轮半径为38.5 m，额定转速为2 rad/s，额定风速为12 m/s，额定功率为1.5 MW，切入风速为3 m/s，切出风速为25 m/s。本文采用基于实际测量值的风速进行模拟，如图3所示为平均输出风速10 m/s的风速。

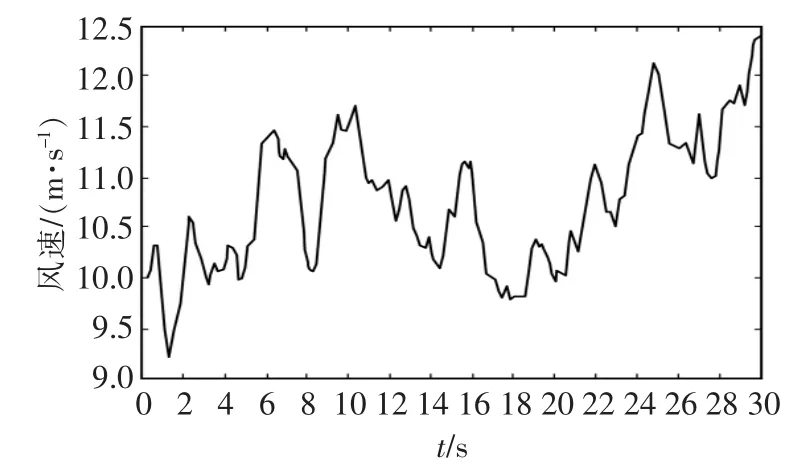
图3 平均风速10 m/s曲线Fig.3 Curve of the average wind speed（10 m/s）

如图4所示为平均风速10 m/s时，风轮转速输出曲线图。风轮转速初始值为0，期望值为2，可看到在控制器作用下，系统在2 s内到达稳定状态。

图4 风轮转速曲线Fig.4 Curve of rotor speed

如图5所示为风轮转速误差曲线图，可以看出，在系统稳定后，相对误差小于5%。说明该控制器具有良好的稳定性能。

图5 风轮转速误差曲线Fig.5 Curve of rotor speed error

如图6和图7所示分别为风轮转速初始值为4.5 m/s和8 m/s下的风轮转速曲线图，图6中的风轮转速初始值在风机正常运行的稳定域内，故系统可以稳定；而图7中的风轮转速从26 s之后开始发散，由于其初始值不在风机正常运行稳定域内，故系统不能稳定。

图6 初值为4.5 rad/s的风轮转速曲线Fig.6 Curve of rotor speed at initial value of 4.5 rad/s

图7 初值为8 rad/s的风轮转速曲线Fig.7 Curve of rotor speed at initial value of 8 rad/s

4 结语

本文通过状态反馈控制对风力发电机组设计了转矩控制器，并计算出了在该控制器下风机正常运行的稳定域。该控制方法设计简单，具有较好的工程应用意义。稳定域的提出为风机的正常工作和使用提供了一定的理论基础。最后通过仿真验证了在风速低于额定风速时，该控制器通过控制转矩，能较好地控制系统，且使系统具有较好的稳定性能。并验证了稳定域的正确性。这对今后风电机组控制器的设计具有指导性意义。

[1]朱瑛，程明，花为，等.考虑损耗转矩的风力发电系统最大风能跟踪控制[J].中国电机工程学报，2013，33（19）：39-46.

[2]罗承先.世界风力发电现状与前景预测[J].中外能源，2012，17（3）：24-31.

[3]蔺红，晁勤.直驱式风电机组建模及最大功率跟踪控制[J].水力发电，2010，36（1）：86-88.

[4]韦徵，陈冉，陈家伟，等.基于功率变化和模糊控制的风力发电机组变速变桨距控制[J].中国电机工程学报，2011，31（17）：121-126.

[5]姚骏，赵磊，刘奥林，等.基于模糊比例-微分控制的永磁直驱风电机组频率调节[J].电网技术，2014，38（11）：158-165.

[6]倪焕山，康戈文.基于模糊算法的智能变桨距控制技术[J].兵工自动化，2011，30（8）：78-80.

[7]何玉林，黄帅，苏东旭，等.变速风力发电机组最大风能追踪与桨距控制[J].控制工程，2012，19（3）：163-166.

[8]Miller A，Muljadi E，Zinger D S.A variable speed wind turbine power control[J].Energy Conversion IEEE Transactions on，1997，12（2）：181-186.

[9]BELTRAN B，AHMED-ALIT，BENBOUZID M.High-order sliding-mode control of variable-speed wind turbines[J].Industrial Electronics，IEEE Transact-ions on，2009，56（9）：3314-3321.

[10]任海军，何玉林，杜静，等.变速变桨距风力机功率控制策略[J].电网技术，2011，35（8）：59-63.

[11]赵微微，张磊，井延伟.变桨风力发电机组控制器优化设计[J].电网技术，2014，38（12）：171-175.

[12]刘军，何玉林，李俊，等.变速变桨距风力发电机组控制策略改进与仿真[J].电力系统自动化，2011，35（5）：82-86.

[13]王利兵，毛承雄，陆继明，等.基于反馈线性化原理的直驱风力发电机组控制系统设计[J].电工技术学报，2011，26（7）：1-6.

[14]梁立哲，姚兴佳，祝贺，等.风力发电系统最大风能追踪的非线性控制策略[J].华东电力，2013，41（2）：114-119.

[15]陈虎，马建光.基于MATLAB的风力发电机组建模和仿真研究[J].节能技术，2012，30（1）：24-28.

[16]CORRADINI M L，IPPOLITI G，ORLANDO G.Fully sensorless robust control of variable-speed wind turbines for efficiency maximization[J].Automatica，2013，49（10）：3023-3031.