基于BP网络的电涡流传感器非线性补偿

（天津理工大学 自动化学院，天津 300384）

电涡流传感器在缺陷检测、状态检测和位移量检测中得到了广泛应用。在位移量的检测中，一般希望仪表的刻度方程是线性方程，以保证仪表在整个测量范围内灵敏度相同[1]。但传感器输出特性大都为非线性，并且常受各种环境参数影响，为保证测量仪表输出与输入之间的线性关系，同时保证传感器的测量值尽可能地接近真实值，则需要对传感器进行非线性补偿。

本文是基于神经网络和Multisim对电涡流传感器进行非线性补偿，为取得精确输出，在Multisim软件中画出电路图、仿真出神经网络训练时的理论输出；在Matlab中运用神经网络的各种函数编写m文件，对神经网络进行训练、测试，计算出补偿之后的结果，与最小二乘法拟合结果进行比较，突出神经网络补偿的效果，并显示出较高补偿精度[2]。

1 电涡流传感器模型的建立与分析

为分析方便，将被测导体上形成的电涡流等效为一个短路环中的电流，这样，线圈与被测导体便等效为相互耦合的2个线圈。电涡流传感器的电路原理如图1所示。

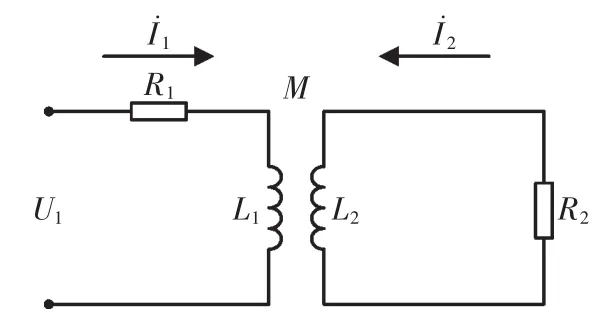
图1 等效检测电路模型Fig.1 Equivalent detection circuit model

图中U1为加在线圈上的激励电压；M为线圈与被测体之间的互感；L1为传感器线圈等效电感；L2为被测体的等效电感；R1为传感器线圈等效电阻；R2为被测体的等效电阻；I˙1为检测线圈中的电流；I˙2为被测体中等效电流。

当被测体与检测电感线圈相对距离发生变化时，检测线圈与被测体涡流环之间的互感M发生变化，从而引起输入电流I˙1的变化。由吉尔霍夫电流定律KCL和电压定律KVL可得到如下方程：

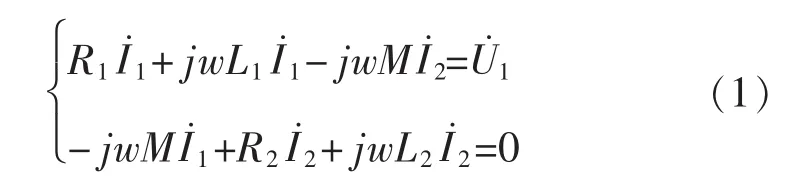
由此可求出线圈受金属导体影响后的等效阻抗，等效电感和品质因数为

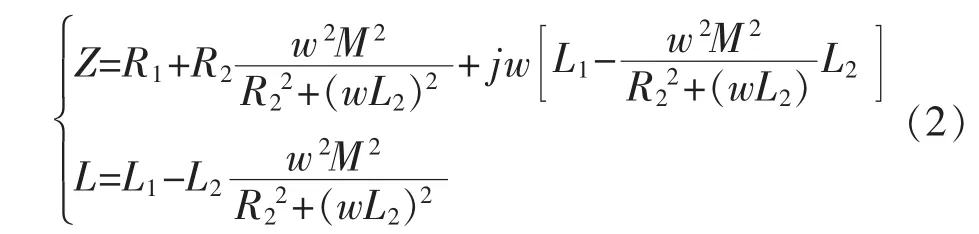
由式（2）可知，线圈金属导体系统的阻抗和电感都是该系统互感系数平方的函数。而互感系数又是距离x的非线性函数。因此，当构成电涡流式位移传感器时，Z=f1（x）、L=f2（x）都是非线性函数。 但在一定范围内，可以将这些函数近似地用一些线性函数来表示，于是在该范围内通过测量Z和L的变化，就可以线性地获得位移的变化[3-5]。

2 关于测量电流分析

根据电涡流传感器的基本原理，将传感器与被测体间的距离变换为传感器的等效阻抗Z、电感L以及Q值3个参数，用相应的测量电路（前置器）来测量。

本实验的涡流变换器为恒频调幅式测量电路，电路原理如图 2 所示，组成为①Q1、C1、C2、C3组成电容三点式振荡器，产生频率为1 MHz左右的正弦载波信号。电涡流传感器接在振荡回路中，传感器线圈是振荡回路的一个电感元件。振荡器作用是将位移变化引起的振荡回路的Q值变化转换成高频载波信号的幅值变化；②D1、C4、L3、C6组成了由二极管和LC形成的π形滤波的检波器。检波器的作用是将高频调幅信号中传感器检测到的低频信号取出来；③R8、Q2、R9构成低频放大电路。

图2 测量电路原理Fig.2 Principle diagram of the measurement circuit

采用Multisim软件求出理论输出，通过在实验中测出每隔0.1 mm时电涡流传感器的输出电感，然后在软件中通过改变可调电感的大小来测出此时的输出电压，最后得到Y=0.729X的输出直线，用此直线作为电涡流传感器的理论输出特性曲线[6]。

3 基于BP神经网络的补偿及比较

3.1 补偿原理

BP网络是一种多层前馈型神经网络，网络结构为1个输入层、1个输出层、若干个隐层，每层由多个神经元组成。BP网络学习规则的指导思想是对网络权值和阈值的修正要沿着表现函数下降最快的方向（负梯度方向）。但是这种方法收敛速度过慢，所以采用Widrow-Hoff学习规则改进神经网络算法，其误差和调整算法为

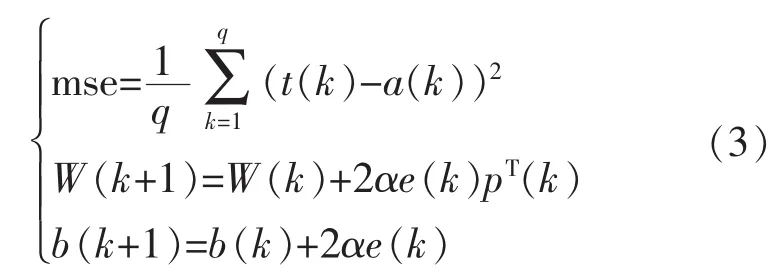
式中：t为相应的期望值输出；a为网络输入；e为训练误差；b为阈值；α为学习率；从式（3）可以看出，它是二次方程，为使收敛速度更快，可以进行2次求偏导，进而得出更快的收敛速度。

具体的补偿校正过程分为离线训练及在线测试2个阶段，在离线训练阶段，令电涡流传感器中的活动衔铁位移每隔0.1 mm变化一次，测得传感器补偿前的实际输出，将两者作为神经网络的输入，并将传感器的理想输出值作为神经网络的输出z，然后利用以上标定数据作为学习样本训练神经网络，从而得到满足一定误差要求的神经网络权值参数；在测试阶段，当电涡流传感器中的活动衔铁位移处于不同位置时，利用之前训练阶段的神经网络权值等参数计算并得到对应输出值，从而实现对当前电涡流传感器输出的有效补偿[7]。

3.2 非线性补偿仿真结果

1）误差下降曲线训练结果

实验里的数据采集如表1所示，从表1中调用80%的数据进行有效训练，可得误差训练曲线如图3所示。

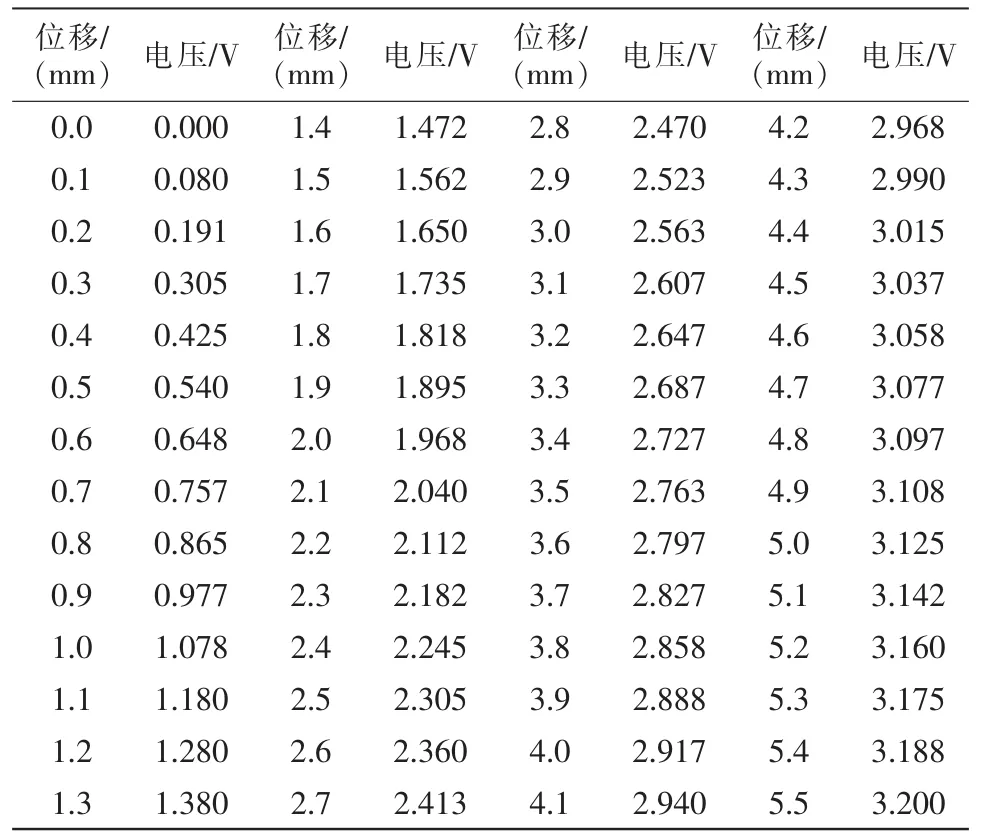
表1 电涡流传感器位移X与输出电压数据Tab.1 Eddy current displacement sensor data X and output voltage

图3 训练误差曲线Fig.3 Training error curve

从图3可以看出：经过215次迭代，误差是0.0000978，而目标为0.0001，体现出达到目标的快速性。

2）对神经网络进行测试

首先选择测试样本，此仿真选择的样本是在训练中没有运用到的样本，p_test=（1.0 1.5 2.0 2.5 3.0 3.5 3.9；1.078 1.562 1.968 2.305 2.563 2.888），测试结果如图4所示。

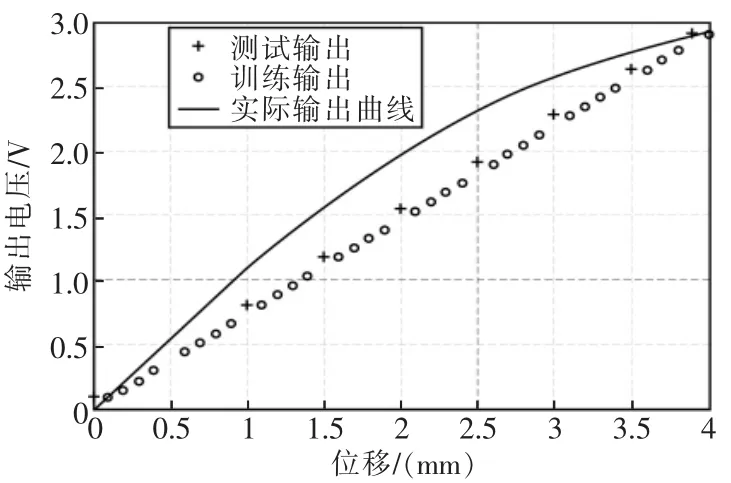
图4 测试结果Fig.4 Test results

从图4可以看出神经网络补偿后的输出误差大大降低，证明神经网络可大大降低非线性误差[8]。

3）基于BP网络的补偿与最小二乘法结果比较

从图5可以看出，基于BP神经网络的补偿效果要优于最小二乘法的效果。

图5 神经网络的补偿结果与最小二乘法结果比较Fig.5 Neural network compensation results compared with the least-square method

通过仿真可知，基于神经网络的补偿能够最大程度地提高电涡流传感器的输出线性度，提高准确度，使最大引用误差下降为0.3725%，加大了电涡流传感器的输出电压值的可信度。同时，也为其他类型的传感器的非线性补偿提供了依据和理论基础，具有很高的使用价值[9-10]。

4 结语

在以前的论文中大多运用最小二乘法去拟合其理论特性曲线，而本文是采用了Multisim和Matlab软件求出其理论特性曲线，这样极大地提高了准确率。在最后也对2种方法做了比较，得出了基于神经网络的算法能够大大改善电涡流传感器的输出特性。采用的电涡流传感器输出转换电路的设计也具有一定的特点，它采用了电容式三点振荡电路来激发1 MHz的高频电压，电路得到简化，准确度也得到了提高。而且还可以自由地调节电容C1和C2的参数来改变振荡电路的频率，以满足使用者的需求。

[1]付丽辉.差动传感器残余电压及非线性的神经网络补偿[J].仪表技术与传感器，2013（8）：15-27.

[2]梁森，欧阳三泰，王侃夫.自动检测技术及应用[M].北京：机械工业出版社，2012.

[3]赵君，王旭.电涡流传感器工作稳定性的技术研究[J].呼伦贝尔学院学报，2013，21（3）：107-112.

[4]童诗白，华成英.模拟电子技术基础[M].北京：高等教育出版社，2010.

[5]徐秉铮.神经网络理论与应用[M].广州：华南理工大学出版社，1991.

[6]张媛媛，徐科军，许耀华，等.PSO算法结合BP神经网络在传感器静态非线性校正中的应用[J].计量学报，2009，30（6）：526-529.

[7]SIMON HAYKIN.神经网络学习[M].北京：机械工业出版社，2011.

[8]冯少辉，周平，钱峰.一种确定神经网络初始权值的新方法[J].工业仪表与自动化装置，2006（1）：65-68.

[9]胡伍生.神经网络理论及其工程应用[M].北京：测绘出版社，2006.