凸函数在初等不等式中的应用

凸函数在初等不等式中的应用

文/磨雪梅

摘要：凸性是函数的一个重要性质。对函数凸性的研究, 特别是在不等式的推导方面很有用处。近年来在高考命题的边缘也涉及了凸函数的一些初步理论。

关键词：凸函数;应用;不等式

中图分类号:G613.6文献标志码：A

1. 引言

凸函数是一类重要的函数，它在许多相关学科里都有着重要的应用。对函数凸性的研究,特别是在函数图形的描绘和不等式的推导方面,凸函数起着十分重要的作用，在高考命题的边缘也涉及了凸函数的一些初步理论。本文主要介绍了凸函数的定义,接着根据定义引出了著名的琴生不等式,运用凸函数在初等不等式的证明方面列举了一些例子如一般的算术不等式、指数不等式、对数不等式等来说明在其中的应用，包括列举了个别高考题利用凸函数来解是相当简便的。

2. (1) 凸函数的定义

(2) 关于凸函数的一个重要不等式——Jensen 不等式

凸函数的推广(Jensen 不等式) (J·L·W·V·Jensen丹麦数学家，1859～1925年)，利用它可以解决许多最值问题且比较方便。下面给出它的内容。

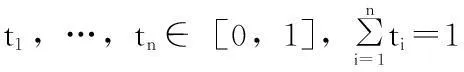
Jensen 不等式是凸函数的一个重要性质,因为每个凸函数都有一个Jensen 不等式,因而它在一些不等式证明中有着广泛的应用，下面我们会举例来说明这一点。

3. 凸函数在初等不等式证明中的应用

例1(94全国文科高考题)

凸函数的概念及性质定理是中学数学的边缘知识，因此，探讨和总结凸函数的性质及应用，对于深刻理解和牢固掌握函数的概念和性质，培养学生抽象思维和创新意识具有重要作用。

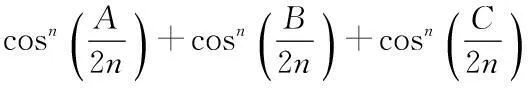
类似的不等式还有:A,B,C是三角形的三个内角,则有:

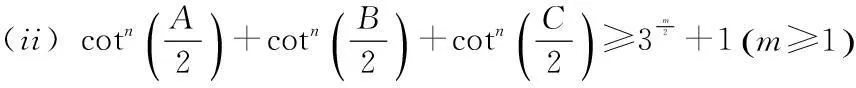
用凸函数来解决不等式问题时,关键是找到相关的凸函数,大多数情况下是容易找的,但是有的情况需要进行变换或变形,如例2。

4.结束语

可以看出,凸函数在推导初等不等式方面是十分有用的，本文简洁、清晰地揭示了凸函数的内涵与外延。介绍了应用广泛的琴生不等式和应用，文章结尾通过利用凸函数来解决一些实际问题,即证明了若干初等不等式,使解题方便快捷。借此说明了凸函数在不等式证明中的作用和研究凸函数的重要性,使本文的探讨具有一定的意义。

(作者单位：广西南宁市新阳西路学校)

参考文献：

[1]浦义书,陈露.凸函数概述.高等数学研究.西北工业大学出版社.2006.7.P34-P36

[2]王新力.琴生(Jense)不等式的应用.杭州教育学院学报,Vo1.19,No.3,May.2002.P10-P13

[3]孟杰.凸函数的基本概念[J].数学通讯.1983.4.P2-P4

[4]陈秋华.也谈利用凸函数证明初等不等式.高等数学研究.西北工业大学出版社.2006.9.P40-P42 .