高中数学不等式易错题型及解题技巧

文/李严

高中数学不等式易错题型及解题技巧

文/李严

摘要：分析高中不等式知识点易错题型,并分类总结,然后给出解题技巧并用实例加以说明,以期对高中不等式的教学起到一定的促进作用。

关键词：高中数学；不等式；易错题；解题技巧

中图分类号：G634.6

文献标志码：码：A

文章编号：号：2095-9214(2015)08-0050-01

不等式是高中数学重点和难点,每年在高考试卷中所占比例也较大,往往结合数列以压轴题的形式出现,是易错点之一,笔者结合自己的教学实践对不等式的易错题型进行了总结,并给出了一些解题技巧和思路。

1.与线性规划结合问题

这类题型在高考数学中占比例较大,考察知识点较多,包括最值、定义域、面积计算等,若没有准确理解不等式及线性规划的性质,容易出错。

A：-1B：-1/2C：1/2D：1

此题的难点和易错点在于三条直线所的围成的图形示意图以及三角形面积的计算。解题思路是先画出三条直线的示意图,如图1所示,然后把四个选项代入即可得答案为B。

图1　例1直线示意图

解答此类题型的技巧主要有两个：

a,求目标函数的最值问题,关键是准确画出可行域,理解目标函数的几何意义

b,目标函数中设置参数,旨在增加探索问题的动态性和开放性,从目标函数的结论入手,从图形的动态分析,对变化过程中的相关量的准确定位,是求解这类问题的主要思维方法。

2高次不等式的解法

高次不等式易错点主要是容易遗忘特殊点(特殊区域)以及判断不准函数的升降。

例2：求(x+3)·(x-2)·(x-4)≤0解集。

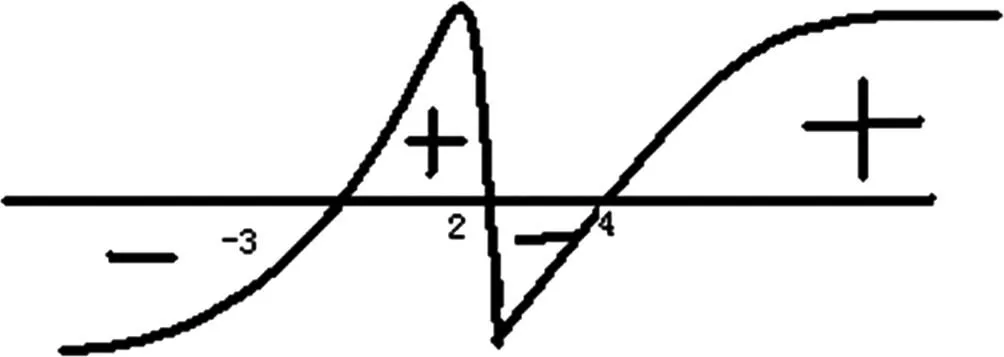
图2　函数曲线示意图

解题思路：

a,先在数轴上标出方程的3个零点,3个零点-3,2,4把数轴分成4个区间,如图2所示。

b,最右的第一区间为正,以后正负相间,在区间标明正负号

c,不等式小于等于零的解找标有负号的区间,得解

d,所以该不等式的解集为{x丨2≤x≤4或x≤-3}

解答此类题型的技巧是擅长使用函数图线简图来划定区间,并注意一些特殊点。

3.含参不等式问题

往往需要对参数进行分类讨论,选择合理的分类依据进行完成。(参数是否为零等,不重不漏)

例3解关于x的不等式ax^2-2x+1>0(a为常数,a∈R)

此题要分情况来讨论,分别是a=0、a>0和a<0三种情况,同时在a>0时还要区分△的值。

此类题型的解题技巧是要牢记参数要对参数进行分类来说明,保证不重不漏。

基本不等式：凑项,拆项,配系数,换元,取倒数,“1”的代换

4.解绝对值不等式

解绝对值不等式主要通过同解变形去掉绝对值符合转化为一元一次或一元二次不等式(组)进行求解,含有多个绝对值符合的不等式,一般可用零点分段法求解,但利用实数绝对值得几何意义求解较便捷,对于最值问题也可以考虑绝对值三角不等式。核心思想是“想方设法”将其转换成不含绝对值的式子求解。

5.不等式恒成立问题

不等式恒成立问题往往与数列或抽象函数相结合来命题,这类问题是高中不等式问题的难点,而且由于抽象性较强,极易出错。

例4(2014年陕西高考数学卷23题)

设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数。

(Ⅰ)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式；

(Ⅱ)若f(x)≥ag(x)恒成立,求实数a的取值范围；

(Ⅲ)设n∈N+,比较g(1)+g(2)+…+g(n)与n﹣f(n)的大小,并加以证明。

该题的考点是结合不等式、函数导数求闭区间上函数的最值并研究函数的单调性。

解答此类题型的技术往往采取分离变量或适当变形,或变换主元,或构造函数,再利用函数的单调性或基本不等式进行求解；最值问题常常转化成利用基本不等式求解。同时在转化不等式中要注意不等式不等号的方向,注意“一正,二定,三相等”。

结束语

笔者结合自己的教学实践,阐述了不等式知识点的易错题型,除了上面论述的之外,不等式的证明、不等式的转换、不等式的最值等问题也容易出错,任课教师需要在讲解时注意。

(作者单位：陕西省渭南市杜桥中学)

参考文献：

[1]张惠淑.高中数学不等式高考试题分析与教学策略研究[D].天津师范大学,2012.

[2]钱煜.基于高考试题的高中数学不等式教学研究[J].语数外学习(高中数学教学)2014(12).