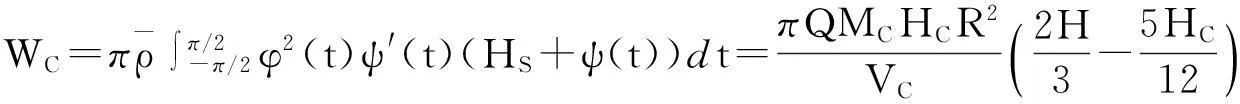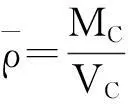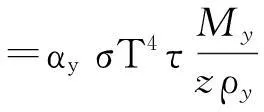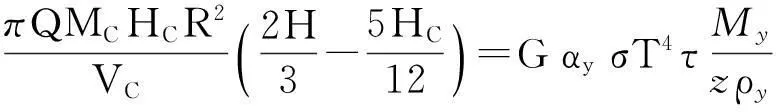基于泛函极值问题的树冠形状分析
基于泛函极值问题的树冠形状分析
刘易成
(国防科学技术大学理学院, 长沙410073)
[摘要]为了培养工科研究生学习泛函分析课程的兴趣,激发利用泛函分析知识解决实际问题的潜能,巩固课堂教学效果,本文将树冠形状的刻画问题中的建模过程细化、简化,提炼成适合研究生课堂教学的教学案例.这种体现数学思维过程的案例可激发研究生学习数学知识的兴趣和培养自主思考的创新能力.
[关键词]泛函极值; 树叶质量; 树冠形状; 案例分析
[收稿日期]2014-10-13
[基金项目]国防科技大学研究生数学公共课一流课程体系建设项目
[中图分类号]O177.1[文献标识码]C
1问题背景
在《泛函分析基础》课程中,泛函的极值问题是一个重点教学内容,也是一个教学难点.为了培养工科研究生学习泛函分析课程的兴趣,激发利用泛函分析知识解决实际问题的潜能,巩固课堂教学效果,根据我们的研究结果[1],将树冠形状的刻画方法提炼简化为教学案例.
事实上,诸多科学工程问题都可以归结为求解给定泛函的极值问题.例如,飞行器的最优轨道确定问题可以归结为求解给定能量泛函的极小值问题;动态系统的最优控制问题以及极小曲面问题(肥皂泡)等等.在此,利用泛函极值讨论树冠形状相关的问题.
树木是我们身边常见的植物,几乎影响着我们一切生活,比如坐的凳子、睡的床是木材做成的,吸入的氧气是树叶释放的等等.树冠的外形与哪些因素密切相关阔叶林为什么多生长在热带区域,而针叶林却在热带区域很少见为寻找这些问题的答案,通过建立树冠外形的预测模型,利用能量守恒原理定性解释部分问题.
2案例分析与建模
由于每片树叶为获得最佳光照效果,都会尽可能暴露于外表面,并减小重叠区.因此,假设树冠的外表面积越大,树叶获得的光照时间就更多.从而树冠的外形可以看成是在给定树冠质量条件下,如何使树冠外表面积最大化而确定的.此时,可以通过建立泛函的条件极值模型确定树冠的外形.假设树的高度为H米,树冠的高度为HC米,树干的平均密度为ρ千克每立方米.
由于树冠的外表面积越大,树叶暴露在外的面积越大.当树冠质量给定后,可以看做是树冠的体积给定.因此在树冠体积固定条件下,树冠的外形由外表面积最大化确定.由于树冠是轴对称的,假设树冠外表面由平面曲线旋转而得.记该平面曲线(简单曲线)的参数方程为
x(t)=φ(t),z(t)=ψ(t),t∈[α,β],
则树冠的体积为
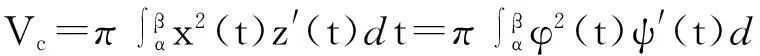
同样,由旋转曲面的表面积计算公式可得
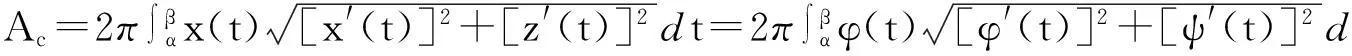
为了确定树冠的外形,必须计算出φ(t)和ψ(t)的表达式.为此,将树冠的外形化为如下优化问题求解.
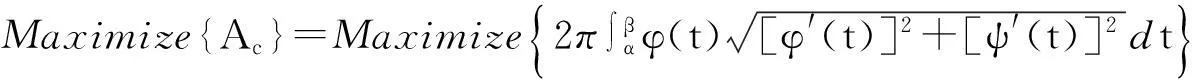
(1)
约束条件为
(2)
为了求解优化问题(1)和(2),利用求解泛函极值的欧拉-拉格朗日方法.为此,引入拉格朗日乘子λ,定义拉格朗日函数:
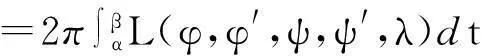
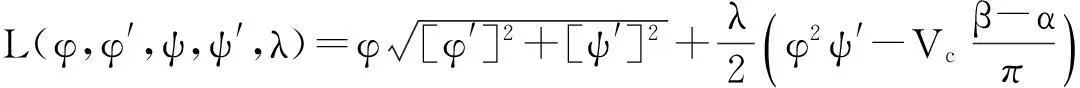
注意到
利用欧拉-拉格朗日方法,树冠外形优化问题可转化为如下欧拉-拉格朗日方程:
化简后可得
另外,曲线满足边值条件:
φ(α)=α0, φ(β)=β0;ψ(α)=α1, ψ(β)=β1.
由此可知,树冠的外形由上述微分方程边值问题确定.然而,直接求解上述微分方程边值问题是一件很困难的事.为此,仅讨论几种常见树冠外形的样式.
2.1 旋转心形面
首先,假设树冠由倒心形曲线绕中心轴旋转而得. 记该曲线的极坐标方程为
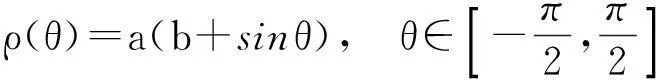
其中a,b为给定常数.由此可知
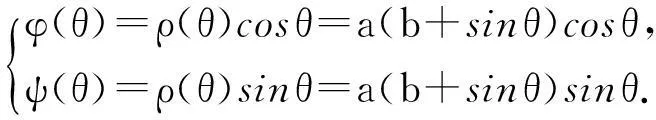
利用数学软件(Mathematica)可计算出此时树冠的外表面积
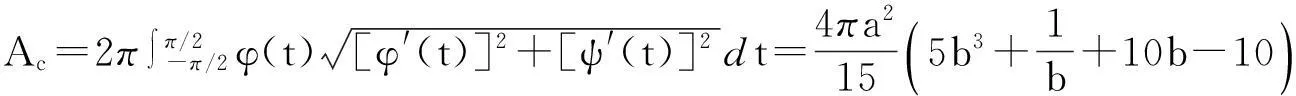
同样可计算出树冠的体积为
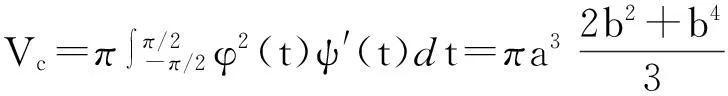
注意到约束条件
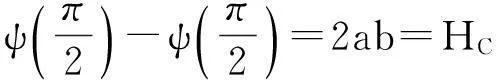
求解以上两个方程可得
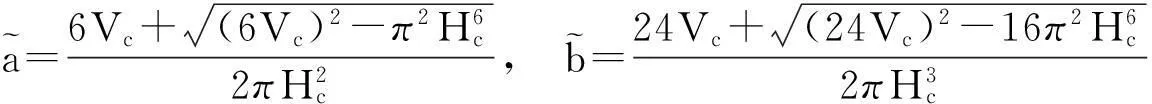
因此,这种情形下,树冠的形状由曲线
唯一确定.
2.2 旋转椭球面
其次,假设树冠由椭圆曲线绕中心轴旋转而得. 记该曲线的极坐标方程为
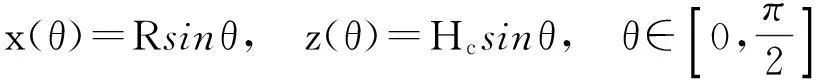
其中R,Hc为给定参数(R 与 因此参数R,Hc满足关系式 因此,这种情形下,树冠的形状由曲线 唯一确定. 3进一步讨论 首先确定整棵树的质量.设树干在高为h米处的横截面积为S(h)平方米. 设树干的密度为ρ千克每立方米,承载的最大压强为P(h) 牛每平方米. 考虑树干的高度从h变到h+Δh, 则横截面积由S(h)变到S(h+Δh). 基于原料最省原理,横截面积的变化量 ΔS=S(h+Δh)-S(h). 正好承载树干发生的重量变化量ΔG. 一方面,ΔG=-ΔS·P(h). 另一方面, ΔG≈S(h)·Δh·ρ·g, 其中g为重力加速度. 因此, 令Δh趋于零, 可得 记地表面的横截面为S0, 即S(0)=S0, 则树干的横截面积满足如下柯西问题 直接求解可得 为了计算树的质量,将树枝、树叶的质量看成是集中于树干.此时,树干的高度将是无穷大.因此树干的总质量为 从而树冠的质量就是 接下来,从能量角度讨论树冠外形的大小与气候带的关系.以椭球树冠为例:假设树冠的质量分布是均匀的.树的各个部分(树叶、树枝等)所需的养分都是通过光合作用完成的.从能量守恒的角度来看,光合作用储存的能量应与从地面将养分输送到树冠所做的功相当.首先,输送养分所做的功为 另一方面,根据Stefan-Boltzmann原理[2], 单位时间内单位面积的树叶通过光合作用可转化的能量为 Jy=αyσT4, 其中αy为转化率, σ=5.67×10-8W·m-2·K-4,T表示温度.因此,树叶光合作用的总能量为 其中My表示总质量,ρy表示树叶平均密度,τ表示光合作用时长,z表示树叶的厚度. 鉴于能量守恒原理, 可以给出光合作用转化能量J总与做功WC之间的关系: WC=GJ总, 其中G为比例常数.因此,对于椭球树冠,有如下等式 该公式蕴含树叶的厚度和气候带(温度刻画)之间的关系:当其他参数固定时,树叶的厚度随温度增加而增加.这可以解释为什么大部分具有又大又厚树叶的树种常常生长在热带的原因. 4结论 树冠的形状形形色色,如何确定树冠外形看似与数学关系不是很密切的问题.但事实上,通过合理抽象,将树叶暴露最大化转化为树冠外表面积最大化,进而转化为体积固定,表面积最大化的条件极值问题.进一步,在能量守恒的观点下,定性解释了为什么具有又大又厚树叶的树种常常生长在热带的原因. 这种解决问题的思路有助于研究生在课程学习阶段接受和自觉应用.可激发研究生学习数学知识的兴趣和培养自主思考的创新能力. [参考文献] [1]Wu J, Liu Y C. Mathematical models to estimate the mass of leaf and sketch the shape of tree[J]. Mathematical Modeling and Analysis, 2013, 18(2): 236-249. [2]Cole George H A, Woolfson M M. Planetary Science: The Science of Planets Around Stars (1st ed.)[M]. Avon, UK: Institute of Physics Publishing, 2002. Analysis of the Crown Shape Based on Functional Extreme Value Problem LIUYi-cheng (College of Science, National University of Defense Technology,Changsha 410073, China) Abstract:In order to develop the interest in learning the course of functional analysis for such graduates in engineering fields, to excite their innovation potential to solve practical problems using the functional analysis knowledge, to evaluate the effect of classroom teaching, in this paper, the author posts a teaching case for graduate teaching by simplifying and refining the modeling process in depiction the crown shape. It reflects the mathematical thought in the modeling process and excites the interest of learning mathematical knowledge, and develops the abilities of independent thinking and innovation. Key words: functional extreme value; mass of tree leaf; crown shape; teaching case analysis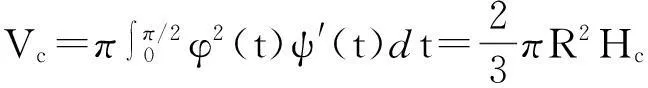
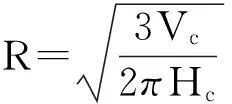
3.1 如何计算树冠质量
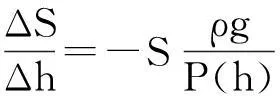
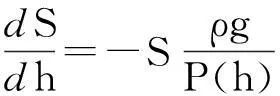
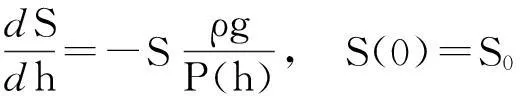
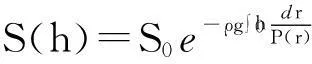
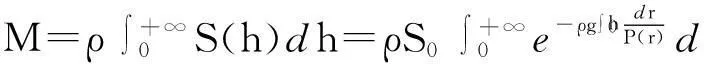
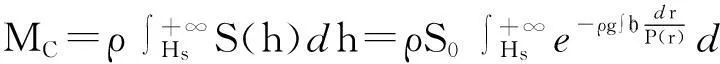
3.2 树冠大小与气候带的关系