具有频率依赖性耦合的神经振子群相响应同步

具有频率依赖性耦合的神经振子群相响应同步

高洋

(合肥工业大学数学学院，合肥230009)

[摘要]考虑频率依赖性耦合神经振子群在外部谐波刺激下的动力学模型，引入相位概率密度函数导出序参数的演化方程.数值模拟结果表明，当固有频率的众数较低时，频率依赖性耦合对神经振子群相响应同步无显著影响；而当固有频率的众数较高时，频率依赖性神经振子群在外部弱刺激下几乎达到完全相位同步，随着刺激强度的增加转为无规则的振荡，最终达到同步周期振荡.

[关键词]神经振子群; 频率依赖性; 序参数; 相响应曲线; 谐波刺激

[收稿日期]2015-01-10

[基金项目]国家自然科学基金(11172086)

[中图分类号]O211[文献标识码]A

1引言

耦合振子集群的同步现象在许多领域(从物理学到工程学)都有着广泛的应用[1-2]，在众多的生物功能中，同步现象更是起到了至关重要的作用，大量的实验表明神经系统的各种戒律活动与神经元之间复杂的相互作用有关[3]，而一些异常的神经疾患，例如帕金森氏症、癫痫等[4-6]，也与神经同步振荡活动有着密切的关系.因此同步现象的研究一直都广受关注.

普遍认为，Kuramoto模型以及它的变体是研究耦合振子群的重要工具，而且已经有了相当多的成果.而最近的许多工作发现了人类活动中其实也有许多周期模式[7，8]，例如在[7]中，作者研究了佛罗伦萨郊区35000辆车辆的GPS数据，他发现这些驾驶员看起来好像在绕着某些地理位置周期性的驾驶.因此，若将一个人类简化为一个周期极限环振子，那么Kuramoto模型或许可以用来研究人类丰富的动力学行为，当然我们需要做些改变.

Kuramoto[9]在研究耦合神经振子群模型时，将耦合系数设定为固定不变的常数，这显然与我们所知的常识有点不一样：两个个体之间的相互作用常常会受到每个个体本身特性的影响.例如，将一个电网网络看作一个Kuramoto振子网络，那么两个振子之间的加权耦合系数就会与振子本身的固有频率有关；在社交网络中，相比性格内向的人而言，性格外向的人会更加频繁的联系接触他的邻居，如果我们将两个个体间的联系看作一种耦合，将联系的频率看作耦合强度，那么这个耦合强度必然与每个个体本身的特性有关，这种特性(性格内向与外向)即为人类的某种固有频率[10].在[10]中，Wang and Li并未考虑振子网络对外界刺激的响应，本文将综合考虑在外部周期刺激和神经振子本身的固有频率的作用下，神经振子群的动力学行为.

2数学模型

考虑外部刺激作用下，N个频率依赖性全局耦合神经振子组成的神经元振子群的随机演化模型

(1)

其中i=1，2，…，N，θi，θj分别为神经振子i和j的相位，ωi是神经振子i的固有频率，K是全局耦合强度，F(t)是外部谐波刺激，本文取F(t)=Isin(ct)，I是刺激强度，c是刺激频率，sinθi是相位敏感函数.

为了研究神经振子群的同步振荡活动，引入描述神经振子群活动的序参数

(2)

其中r(t)和φ(t)分别表示随时间变化的平均场幅值和平均场相位，r(t)描述神经振子群的同步化强度，0≤r(t)≤1，r(t)越大表明同步化程度越强.当r(t)=1时，神经振子群处于完全相位同步，当r(t)=0时，神经振子群处于完全不相干状态.由(2)可得

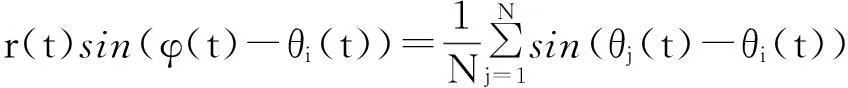
(3)

代入(1)得

(4)

当组成神经振子群的振子数N→∞时，描述神经振子群整体活动行为的序参数可表示为

(5)

其中概率密度函数f(θ，ω，t)描述神经振子集群的状态，即t时刻振子相位和自然频率分别落入区间[θ，θ+dθ]，[ω，ω+dω]的概率为f(θ，ω，t)dθdω，且

当N→∞时，(4)式转换为

(6)

由(6)可知，频率为ω，相位为θ的振子的瞬时速度为ω+Kωβrsin(φ-θ)+F(t)sinθ，从而可得关于f的非线性Fokker-Planck方程

(7)

其中*表示共轭复数.利用Ott-Antonsen假设[12]：

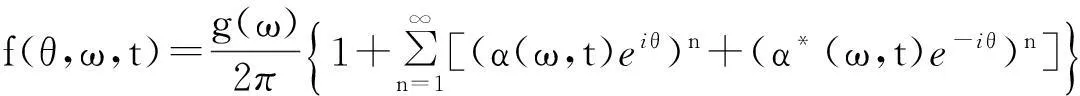
(8)

把(8)代入(5)可得

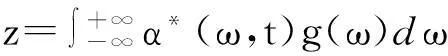
(9)

把(8)，(9)代入(7)可得关于α(ω，t)的演化方程

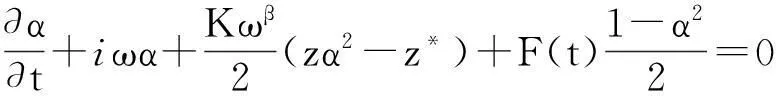
(10)

假设固有频率服从柯西-洛伦兹分布

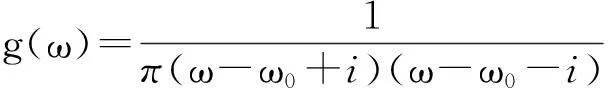
ω0是定义分布峰值位置的位置参数，即固有频率的众数.则由(9)式，得

z(t)=α*(ω0-i，t)，

将其代入(10)，得到关于序参数z的演化方程

(11)

当β=0时(即普通的神经振子群)

将z(t)=r(t)eiφ(t)代入方程(11)，可进一步得到关于序参数的幅值r(t)和相位φ(t)的演化方程

(12)

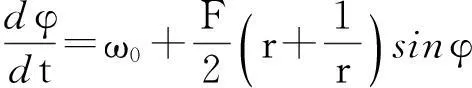
(13)

当β≠0(本文取β=1)时，(即频率依赖性神经振子群)

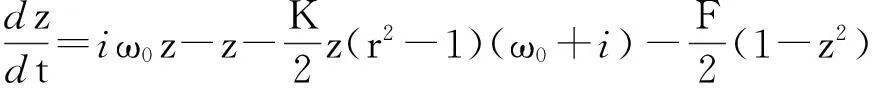
(14)

将z(t)=r(t)eiφ(t)代入方程(14)，可进一步得到关于序参数的幅值r(t)和相位φ(t)的演化方程

(15)

(16)

本文研究的是固有频率和外部刺激对神经振子群活动的影响，所以把全局耦合强度看成一固定的系数，设K=1.用四阶龙格-库塔法求出方程(12)， (13)，(15)，(16)的数值解.

3 数值分析

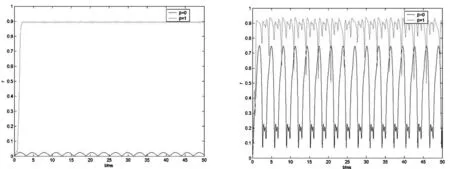
(a) 参数：c=1，ω 0=0.5， I=0.5　　　　　　　　　　　　(b) 参数：c=1，ω 0=0.5, I=5 图1　固有频率的众数较低时，序参数幅值随时间的演化.

图1呈现的是当固有频率的众数ω0较低时，序参数幅值随时间的演化.弱刺激会使神经振子群会产生较弱的同步周期振荡(图1(a))，而随着刺激强度的增加，同步程度也会变高(图1(b)).并且无论是弱刺激还是强刺激，频率依赖性神经振子群与普通的神经振子集群的同步程度都相当.由此可见，当固有频率的众数较低时，两种神经振子群对外部刺激的响应无明显差异.

(a) 参数：c=1，ω 0=10， I=0.5　　　　　　　　　(b) 参数：c=1，ω 0=10, I=10

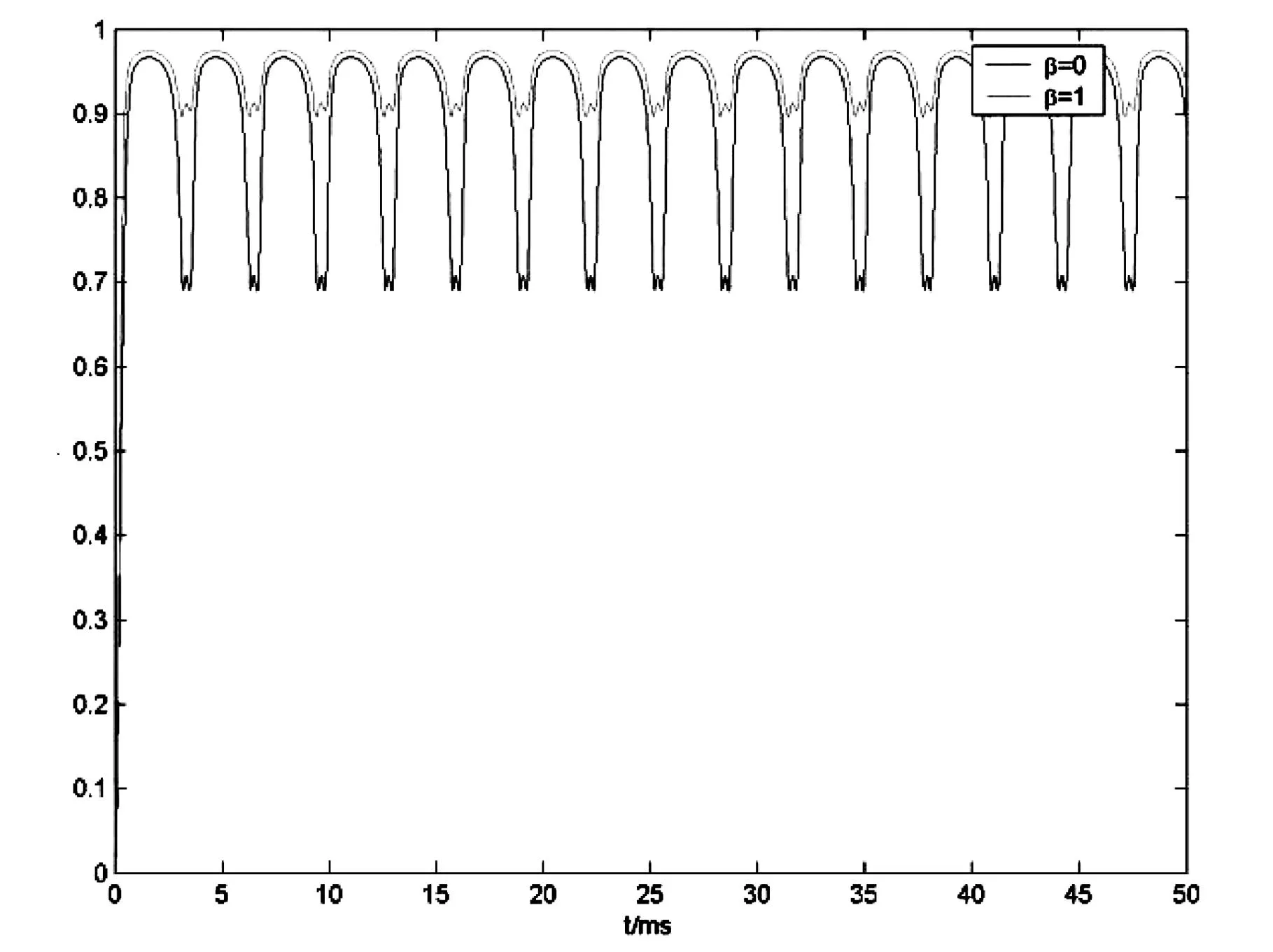
(c) 参数：c=1，ω 0=10, I=30 图2　　固有频率的众数较高时，序参数幅值随时间的演化

图2呈现的当固有频率的众数ω0较高时，在不同的刺激强度下，序参数幅值随时间的演化.在适当的外部频率条件下，对于普通的神经振子群，弱刺激只能使其产生极弱的同步周期振荡活动(图2(a))随着刺激的加强，同步程度也越大(图2(b)，图2(c));而对于频率依赖性神经振子群，弱刺激会使其几乎达到完全相位同步(图2(a))，但在刺激强度增大到与ω0相当的过程中，神经振子群逐渐转向不规则的振荡活动(图2(b))，当刺激强度远超过ω0时，神经振子群则产生极大程度的同步周期振荡活动(图2(c)).由此可见，当固有频率的众数较高时，两种神经振子群对外部刺激的响应具有明显的差异.

4小结

Wang and Li研究的是在不同的固有频率分布及不同的β值条件下，频率依赖性耦合振子群的不同的动力学行为.与Wang and Li研究工作不同，本文考虑的是频率依赖性条件下，神经振子群对外部刺激的响应情况.数值分析结果表明:

(i) 固有频率的众数较低时，外部刺激可使普通的神经振子群产生同步周期振荡活动，且随着刺激的加强，同步程度增大；频率依赖性神经振子群对外部刺激的响应与普通的神经振子群无明显差异.

(ii) 固有频率的众数较高时，普通的神经振子群对外部刺激的响应方式与(1)相同；而对于频率依赖性神经振子群，弱刺激会使其几乎达到完全相位同步，而当刺激的强度与固有频率的众数相当时，神经振子群产生不规则的振荡，继续增强刺激，则会使其产生同步周期振荡活动.

[参考文献]

[1]Kuramoto Y. Chemical Oscillations， Waves， and Turbulence[M]. New York:Springer，1984.

[2]Winfree A T. The Geometry of Biological Time[M].New York:Springer，2001.

[3]Buzsaki G. Rhythms of the brain[M]. UK: Oxford University Press，2006.

[4]Hammod C， Bergman H， Brown P. Pathological synchronization in Parkinson’s disease: networks， models and treatments[J].Trends Neurosci.，2007，30:357-364.

[5]Fries P， Schroder J， Roelfsema P. Oscillatory neuronal synchronization in primary visual cortex as a correlate of stimulus selection[J].J Neurosci.，2002，22:3739-3754.

[6]Lehnertz K. Non-linear time series analysis of intracranial EEG recordings in patients with epilepsy- an overview[J].International Journal Psychophysiology，1999，34:45-52.

[7]Bazzani A， Giorgini S， Rambaldi， Galloti R.Statistical laws in urban mobility from microscopic GPS data in the area of Florence[J].Journal of Statistical Mechanics: Theory Experiment，2010，05:05001.

[8]Wang P， Gonzalez M， Hidalgo C and Barabasi A.Understanding the spreading patterns of mobile phone viruses[J].Science，2009，324:1071-1076.

[9]Kuramoto Y. Collective synchronization of pulse-coupled oscillators and excitable units[J]. Physica D，1991，50:15-30.

[10]Wang H and Li X. Synchronization and chimera states of frequency-weighted Kuramoto-oscillator networks[J]. Phys.Rev.E，2011，83:066214.

[11]Eward O and Thomas M A. Low dimensional behavior of large systems of globally coupled oscillators[J].Chaos，2008，18:037113.

Phase Synchronization of Neuronal Oscillator Networks with

Frequency-Dependent Coupling

GAOYang

(School of Mathematics， Hefei University of Technology， Hefei 230009， China)

Abstract:We explore phase synchronization in a population of neuronal oscillators with a frequency-dependent coupling in the presence of harmonic stimulus by the use of phase response curve. We derived the evolution equation of the order parameter by introducing the probability density function. Numerical simulations show that when the mode of a natural frequency is low， the frequency-dependent coupling has not significant effect on phase response synchronization; and when the mode of the natural frequency is high， complete phase synchronization occurs in the population of neuronal oscillators in weak external stimulation， with increasing stimulus intensity， ultimately achieve synchronous periodic oscillation.

Key words: neuronal oscillators; frequency-dependent; order parameter; phase response curve; harmonic stimulus