超几何分布的数字特征和概率计算的探讨
超几何分布的数字特征和概率计算的探讨
李玉萍1,刘心馨2
(1.郑州师范学院数学与统计学院,郑州450044;2.华中师范大学计算机学院,武汉430079)
[摘要]用定义法、性质法、概率母函数法三种方法探索了超几何分布的数学期望和方差的求法,同时又给出了超几何分布、二项分布、泊松分布和正态分布之间的近似关系,从而解决了超几何分布的概率计算问题.
[关键词]期望; 方差; 概率母函数; 二项分布; 泊松分布
[收稿日期]2015-01-09;[修改日期]2015-05-11
[基金项目]河南省科技厅软科学计划项目 (132400410697)
[中图分类号]O212[文献标识码]C
超几何分布是产品计数抽样检验、可靠性问题中常常遇到的一类重要的数理统计模型.然而国内概率论与数理统计教材中,有的教材给出相关例题,没有提到超几何分布的名称,有的教材只是简单地给出它的定义以及与二项分布的区别.很少有教材涉及到这种分布的数字特征问题,因此本文对超几何分布的数学期望和方差来做进一步的探讨和研究,进一步地为了解决超几何分布的概率计算问题,探索了超几何分布、二项分布、泊松分布和正态分布之间的近似关系.下面给出超几何分布的定义
定义设随机变量X的概率分布为

其中d=max(0,n+M-N),r=min(n,M),则称随机变量X服从参数为n,N,M的超几何分布,
记为
X~h(n,N,M).
1超几何分布的数字特征
1.定义法求期望与方差
(i)

(ii)由于


所以
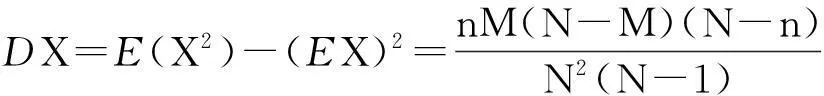
2.性质法求期望和方差
对于超几何分布,构造一个抽产品模型:设N件产品中有M件次品,从中任取n件进行检查,求查得的次品数X的数学期望和方差.
(i) 设
(1)
则



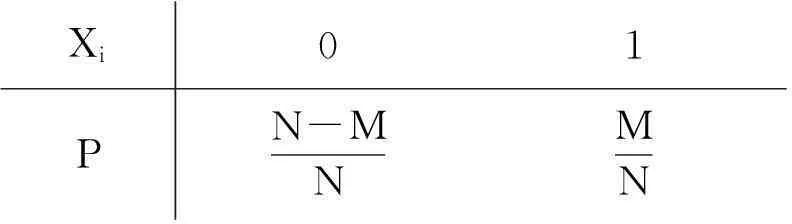
Xi01PN-MNMN
则

故

注① 随机变量和的期望等于期望的和,这里并不要求和中的随机变量相互独立;
② X的分布为

所以X的期望为
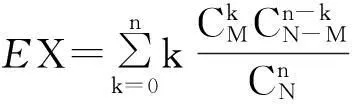
由上面的计算得

③ 若X表示n次有放回地抽取所得次品数,则


(ii)

(2)


(3)
从而对1≤k≤j≤n有

(4)
因此,Xk与Xj的协方差为

(5)
由(3),(5)可以得到服从超几何分布的随机变量X的方差为

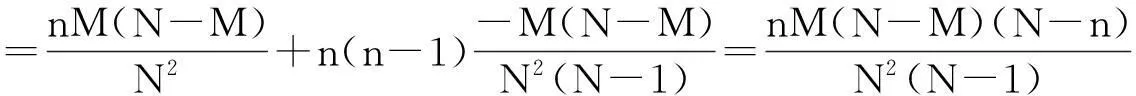
(6)
2概率母函数法求期望和方差
先引入母函数的定义和性质
定义设X是概率空间(Ω,F,P)上定义的N上取值的随机变量,N={0,1,2,…},则称E(tX)为随机变量X的概率母函数,记为

性质 φ′X(1)=E(X),φ″X(1)=E[X(X-1)],Var(X)=φ″X(1)+φ′X(1)-[φ′X(1)]2.
若把超几何分布的概率母函数记为φ(M,N-M,n,t),则

在这里,记(M)[i]=M(M-1)…(M-i+1),φ(M,N-M,n,t)对t求导数得


运用概率母函数的性质得

(7)
(ii)DX =E(X2)-[E(X)]2=φ″(N,M,n,1)+φ′(N,M,n,1)-[φ′(N,M,n,1)]2

(8)
3超几何分布的概率计算问题
对于超几何分布,当抽取的个数n远远小于产品总数N时,每次抽取后,其次品的概率变化很小,即不放回与放回抽样差别不大.于是,n固定,N无限增大,有下面的结论:
定理1
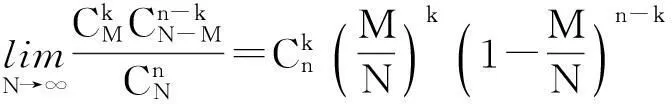
(9)


(10)
当n充分大,p足够小,np的大小适中,二项分布的计算的有关问题可用泊松分布近似计算.
定理3设在独立实验序列中,事件A在各次试验中发生的概率为p (0 (11) 其中x为任意实数,p+q=1. 当n充分大时,服从二项分布的随机变量ηn近似地服从正态分布N(np,npq). 综上,在超几何分布的概率计算问题中,由式(9)知只要N≥10n,就可用二项分布近似计算.而二项分布的概率计算问题中,当n充分大时的计算也相当复杂.由式(10)知,当N≥10,p≤0.1,就可用泊松分布近似计算;当n→∞时,就可用正态分布来近似计算.至此有了三种分布的近似关系,超几何分布的概率计算问题就得到了很好的解决. [参考文献] [1]翟明娟.概率统计中有关超几何分布的一个误解 [J].统计与决策,2014,3(3):26-28. [2]匡能晖.超几何分布的数学期望和方差的定义求法[J].高等教育研究,2010,13(4):73-74. [3]魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社, 2003. [4]李万军,赵白云,秦素萍.概率论与数理统计[M].沈阳:辽宁大学出版社,2007. [5]杨善兵.三种重要的极限分布[J].盐城工学院学报,2003,16(1): 74-75. [6]燕建梁.超几何分布及其推广[J].太原师范学院学报,2013,12(1): 21-23. [7]赵永祥,李丽.超几何概率教学探讨[J].重庆三峡学院学报,2014, 30(151): 32-34. [8]马松林.超几何分布的数学期望和方差的一种新求法[J].巢湖学院学报,2006,8(3):139-140. Explore the Digital Characteristic and Hypergeometric Distribution Probability Calculation LIYu-ping1,LIUXin-xin2 (1.School of Mathematics and Statistics,Zhengzhou Normal University, Zhengzhou 450044,China; 2. College of Computer Sciece and Technology, Central China Normal University ,Wuhan 430079, China) Abstract:Expectation and variance of the hypergeometric distribution is explored by using the definition, the nature and generating function method, and the approximate relationship between the hypergeometric distribution, geometric distribution, Poisson and normal distribution is obtained, which solve the hypergeometric distribution probability calculation. Key words: expectation; variance; Poisson distribution; binomial distribution; probability generating function

