应用实例在高等代数教学中的作用
应用实例在高等代数教学中的作用
曹慧,周蕊,蔺小林
(陕西科技大学理学院,西安710021)
[摘要]针对学生难以理解高等代数中的基本概念, 在高等代数的教学过程中,结合具体教学内容加入一些应用实例帮助学生更好的理解相关概念和体会数学的广泛应用.以讲述矩阵特征值和特征向量为例,除讲解基本概念和计算方法外,结合自己的研究工作介绍了人口模型和传染病模型,给学生展示了特征值和特征向量应用的例子,使得学生对特征值和特征向量有了更深入的理解.
[关键词]矩阵; 特征值; 人口模型; 传染病传染病
[收稿日期]2013-07-29
[基金项目]国家自然科学基金(11301314); 陕西省科技厅自然科学
[中图分类号]O175; 37N25[文献标识码]C
1引言
高等代数课程是数学专业和信息与计算科学专业本科生必修的基础课程之一,熟练的掌握高等代数课程是这些专业的本科生学好后续课程的一个先决条件.现有的高等代数教材[1]大部分都集中在讲述概念、定理和方法,内容都偏于抽象和形式化.如何将这些抽象的知识更好地传授给学生,提高教学质量是很多高校数学专业课教师的目标[2,3].在高等代数课程教学过程中,通过一些应用例子入手,尽量通过具体的应用实例来导出或帮助学生理解抽象的数学概念,这对提高教学质量有着重要的作用.在本文中我们着重以矩阵、特征值和特征向量为例来说明应用实例在高等代数教学中的作用.
在高等代数中,m×n矩阵A就是m×n个数组成的数组,n×n矩阵A的特征值就是特征方程f(λ)=|λE-A|=0 (E是同级的单位矩阵)的根λ1,λ2,…,λn,而特征值λi的特征向量就是齐次线性方程组(λiE-A)X=0的基础解系.特征值就是计算行列式的值,求所得到的多项式方程的根;特征向量是解相应的齐次线性方程组.对这些抽象的概念和形式化的计算过程,学生能够记住和进行规范化的计算.但求特征值和特征向量的过程比较繁琐,学生也不知道他们到底有什么应用,就容易产生厌倦感,影响教学效果.为了激发学生的学习兴趣,使得他们更好地理解和掌握矩阵、特征值和特征向量的概念与知识,我们在教学过程中引入了一些实际应用问题,让学生看到矩阵、特征值、特征向量在解决实际问题中的具体应用,有效地提高了教学效果.下面我们给出了矩阵、特征值、特征向量在研究人口变化和疾病传播过程中的两个应用案例.
2矩阵和特征值在人口模型中的应用
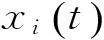
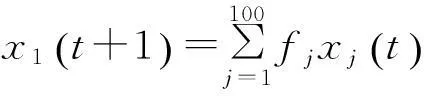
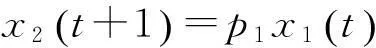
……
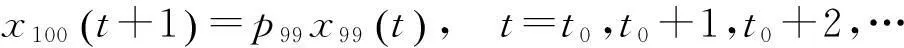
(1)
其中t0表示我们选取的一个初始年份.利用矩阵的形式将(1)表示出
x(t+1)=(F+T)x(t),
(2)
其中

矩阵F中的非零元fj表示各个年龄人口中具有生育能力的个体在单位时间内的生育率,称F为生育矩阵;T中的非零元pj表示年龄为j的个体存活到j+1的比例,称T为转移矩阵.通过矩阵得到的递推关系(2)就是描述人口增长的数学模型.用我国1982年的人口普查数据确定初始值和参数,利用模型(2)进行递推就可以得到我国从1982年以后各年份的人口预测值,通过人口实际统计值和预测值的比较让学生看到模型的作用和预测的误差.
接下来,引导学生分析由模型(2)所描述的人口长久的变化趋势,这就和模型(2)中矩阵F+T的特征值和特征向量相关.通过计算和分析,让学生看到矩阵F+T有惟一的正特征值λ1,并且λ1所对应的特征向量的各个分量都为正.利用特征值和特征向量的关系,让学生明白λ1就是人口的增长率,其对应的正特征向量给出了时间趋于无穷时各年龄组人口的相对比例.利用矩阵特征值和特征向量的知识,很容易得到当λ1<1时,人口趋于零;当λ1>1时,人口趋于无穷.人口趋于稳定的充分必要条件就是λ1=1.这样一来,学生对矩阵、特征值、特征向量的实际背景和应用就有了很好的体会.
为了更进一步让学生看到矩阵的特征值的应用,对模型(2)进行进一步的分析.直接计算可知|E-T|=1≠0,即(E-T)-1存在,并且

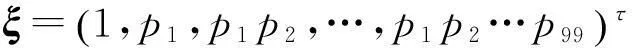
定义p0=1,进一步计算可得

所以矩阵(E-T)-1F特征值分别是0和b,并且可以验证(E-T)-1Fξ=bξ.也就是,ξ是矩阵(E-T)-1F对应于特征值b的特征向量.

3矩阵和特征值在传染病模型中的应用
矩阵和特征值也可以用来描述和分析结核病传播问题.根据世界卫生组织的估计,我国每年大约有130万结核病新发病例,发病人数居世界第二,仅次于印度.结核是我国重点关注的传染病之一,是我国面临的一个严重的公共卫生问题.用模型来描述和预测未来几年我国结核的传播情况有着重要的作用.
S(t+1)=S(t)+Λ-βI(t)-dS(t)+γI(t),
L(t+1)=L(t)+βI(t)-(d+α)L(t),
I(t+1)=I(t)+αL(t)-(d+μ+γ)I(t).
(3)
这里,Λ是单位时间内进入易感者类的人数;d是各类人口的自然死亡率;μ是染病者的因病死亡率;β表示肺结核的传染率;α表示肺结核的发病率;γ表示单位时间内染病者的治愈率.根据问题的实际意义可知,所有的参数非负,且满足d+α<1,d+μ+γ<1. 引入下面的向量和矩阵

将模型(3)写为
x(t+1)=Ax(t)+B.
(4)
根据我国第四次全国结核病流调数据可以确定出2000年我国结核病易感者人数S(0),潜伏感染者人数L(0),染病者人数I(0),以及模型中的参数,利用模型(3)递推计算就可以得到2000年以后各年份我国结核病的易感者人数S(t),潜伏者人数L(t)和染病者人数I(t).
还可以借助矩阵的知识对结核病的发展趋势进行定性的分析.由模型(4)看出,潜伏者和染病者所满足的方程与易感者无关,所以可以引入

从模型(4)得到潜伏者和染病者所满足的递推模型为
z(t+1)=Mz(t),或者z(t)=Mtz(0).
(5)
由模型(5)看出,结核病的传播趋势依赖于矩阵M.矩阵M的特征值对疾病的流行趋势有重要影响.矩阵M的特征方程为|λE-M|=0,其中
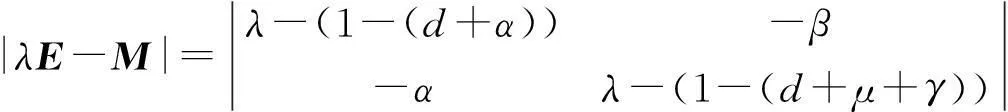
为了使得对矩阵M两个特征根的分析简单一些,令λ=σ+1,则σ满足f(σ)=0,其中
f(σ)=σ2+(d+α+d+μ+γ)σ+(d+α)(d+μ+γ)(1-R0),

对于σ满足的二次方程f(σ)=0,有
Δ=(d+α+d+μ+γ)2-4(d+α)(d+μ+γ)(1-R0)
=((d+α)-(d+μ+γ))2+4(d+α)(d+μ+γ)R0>0.
所以方程f(σ)=0一定有两个实根,分别记为σ1和σ2.即矩阵M一定有两个实特征根,λ1=σ1+1和λ2=σ2+1,σ1和σ2分别为


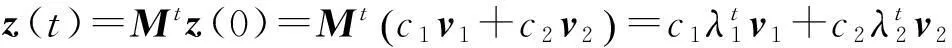
由σ1和σ2的表达式及f(σ)的形式知道,当R0<1时,σ1<σ2<0.又由于
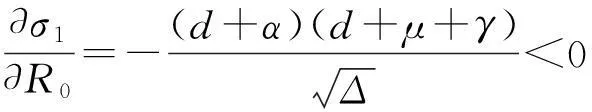
σ1是R0的减函数.且当R0=1时,
σ1=-(d+α+d+μ+γ)>-2.
所以当R0<1时,
-1<λ1=1+σ1<1,-1<λ2=1+σ2<1.
这表明,不管疾病发生时的初始状态如何,当R0<1时,由于矩阵M的特征值都是小于1,随着时间t的变化,疾病一定呈现递减的趋势,也就是最终可以被消灭.另一方面,如果R0>1,则有σ2>0,并且λ2=1+σ2>1.由z(t)的表达式得到,在一些情况下,病人会逐渐增加,引起结核的大爆发.因此,为了有效的控制结核的流行,就需要

这可以通过降低结核的发病率α或者结核的传染率β来实现.
事实上,R0也是某个矩阵的特征值.将矩阵M写为M=F+V,其中
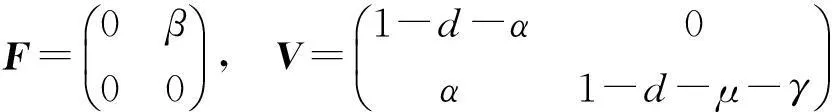
进一步计算可得

显然,矩阵F(E-V)-1的正特征值就是
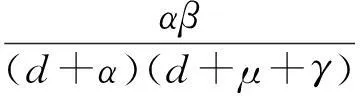
矩阵F和V及R0都有着明确的传染病学解释.R0称为“基本再生数”,R0给出了所有的个体都是易感者时,一个染病者所能感染的人数.R0的大小反映了传染病流行程度的大小.
R0<1与矩阵M模最大的特征值小于1事实上是等价的.这个结论利用矩阵论的相关知识是可以从理论上给出严格的数学证明的,一年级的学生可以借助数学软件Matlab或者Maple数值计算来体会这一结论的正确性.利用我国结核病数据确定模型中的参数值
α=0.005,β=0.223,d=0.006,μ=0.005,γ=0.216.
相应地,矩阵F(E-V)-1的正特征值R0=0.491189<1.另一方面,由这些参数值得到

直接计算M的特征值分别得到λ1=0.766947<1和λ2=0.994053<1.显然,R0<1, |λ1|<1和|λ2|<1同时成立.从这里也可以看到,矩阵F(E-V)-1的正特征值R0有具体的表达式,确定参数后可以直接计算得到.而矩阵M的特征值需要求解一个多项式方程的根,模型的维数高时还有一定的困难.
4结论与认识
高等代数教材中的绝大部分内容都是通过一些公理化语言表述的比较抽象的概念、定理、以及一些形式化的计算过程,这对于刚刚迈入大学校园的本科生而言想要彻底理解和掌握是比较困难的.教师在授课时最好为这些抽象的数学概念和定理给出一些具体的应用例子,使得学生体会这些概念和定理的应用背景,让学生看到这些比较抽象的数学概念、定理和方法的具体应用,帮助学生更好的理解和掌握专业知识,以便为后续专业课程的学习和未来的发展奠定坚实的基础.
本文中我们以矩阵、特征值和特征向量为例,具体给出了它们在研究人口和传染病问题方面的应用.同时,介绍了在教学过程中如何将高等代数的相关理论与这些实际问题的分析结合起来,如何利用数学软件和计算机等工具对数学的理论知识进行实验和体会,让学生更深入的理解应用数学知识解决实际问题的过程,体会数学在解决实际问题中的巨大作用,增强他们学习数学知识和应用数学知识解决实际问题的积极性,以及训练和培养他们应用数学软件的能力.
[参考文献]
[1]北京大学数学系几何与代数教研室前代数小组.高等代数[M].3版.北京:高等教育出版社,2003.
[2]朱用文. 高等代数课程的教学改革[J].大学数学,2012,28(6):1-4.
[3]杨浩菊. 在高等代数教学中渗透数学史知识的思考[J].大学数学,2013,29(2):6-9.
[4]周义仓,赫孝良. 数学建模试验[M]. 2版.西安:西安交通大学出版社,2003.
[5]马知恩,周义仓,王稳地,靳祯. 传染病动力学的数学建模与研究[M]. 北京:科学出版社,2004.
[6]Zhou Y C, Khan K, Feng Z.et al. Projection of tuberculosis incidence with increasing immigration trends [J]. J. Theoretical Biology, 2008, 254: 215-228.
Application Examples in Teaching Advanced Algebra
CAOHui,ZHOURui,LINXiao-lin
(School of Science,Shaanxi University of Science & Technology,Xi’an 710021, China)
Abstract:Most concepts and theorems in advanced algebra are quite abstract and less applicable, which are difficult for freshmen to understand. Application examples in teaching advanced algebra can help students to understand the abstract concept and theorems and their applications. In order to make our teaching more interesting, understandable, and applicable, we have chosen population model and epidemic model as our application examples when we teach matrix, eigenvalues, and eigenvectors. Those models, closely related with our research projects, have given students typical application examples of matrix, eigenvalue and eigenvector. Those examples are very good application which help students to experience the role of mathematics in solving real world problems, and to give students more motivation to learn matrix, eigenvalues, and eigenvectors better.
Key words: matrix; eigenvalues; population model; epidemic model

