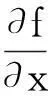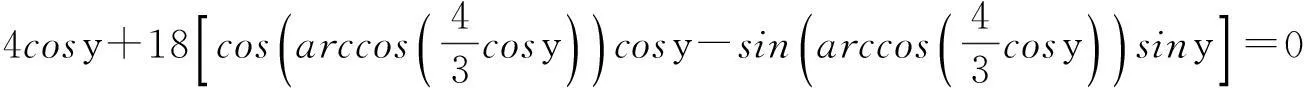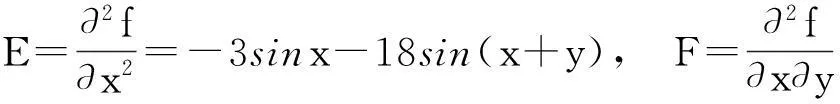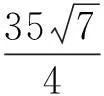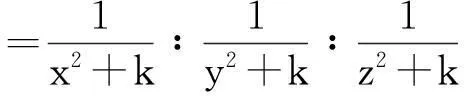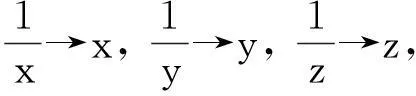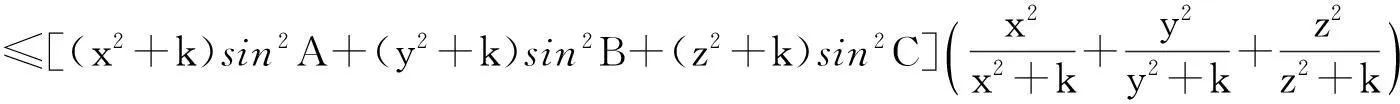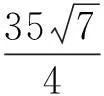一道全国大学生数学竞赛试题的解法及推广

一道全国大学生数学竞赛试题的解法及推广

王永喜1，王泽文1，刘冰2，邱淑芳1

(1.东华理工大学理学院，南昌330013；2. 南昌二中，南昌330038)

[摘要]给出了一道全国大学生数学竞赛试题的三种解答， 在此基础上研究了三角形三内角正弦的线性和最大值问题， 从而推广了竞赛试题中的结论. 最后， 研究了三内角正弦的指数之积以及余弦的指数之积的上界问题.

[关键词]大学生数学竞赛； 三角形； 嵌入不等式； 正弦定理； 余弦定理

[收稿日期]2014-11-15

[基金项目]江西省高等学校教学改革研究课题(JXJG-13-6-7); 江西省青年科学家培养计划(20122BCB23024); 江西省自然科学基金(20142BAB201008)

[中图分类号]O151.2[文献标识码]C

考虑2011年第三届全国大学生数学竞赛(数学类)的一道赛题:

对于△ABC， 求3sinA+4sinB+18sinC的最大值.

解法1该解法是依据全国大学生数学竞赛组委会给出的参考解答给出的， 但有所不同.

三角形三个角A，B，C的取值范围为

(A，B，C)∈D≡{(α，β，γ)|α>0，β>0，γ>0且α+β+γ=π}.

首先， 考虑3sinA+4sinB+18sinC在D的闭包

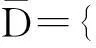
上的最大值. 于是，有

(1)

上述过程与组委会给出的解答稍有不同， 即倒数第二步直接利用Cauchy-Schwartz不等式得到是“≤”成立， 这是因为我们认为用“=”不是直接的.考虑函数

在[0，π]上的最大值问题.对于函数f(C)， 显然有

f(C)≥f(π-C)，∀C∈[0，π/2].

于是， 由微积分中一元函数取极值的必要条件， 得

(2)

(2)式等价于

(8cosC-1)(27cos2C+32cosC+4)=0.

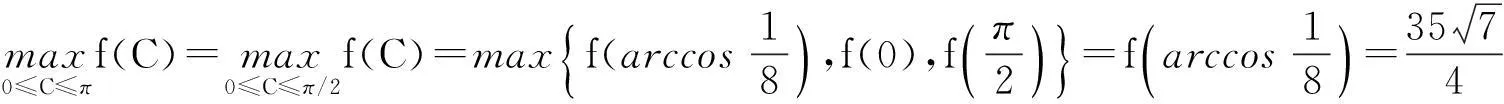
则有t>0且A=arctan(t)∈(0，π/2)⊂[0，π-C]. 因此， 成立

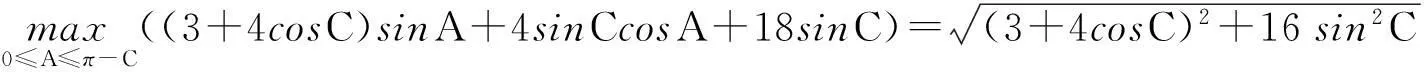
综上所述， 即得

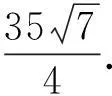
解法2 (配凑法)直接利用Cauchy-Schwarz不等式[1]， 得

3sinA+4sinB+18sinC

=3sinA+4sinB+18sinAcosB+18sinBcosA

=3sinA(1+6cosB)+3cosA(6sinB)+4sinB

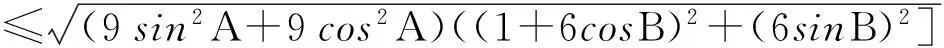
解法3因为0

3sinA+4sinB+18sinC=3sinA+4sinB+18sin(A+B).

为此， 在区域(0，π)×(0，π)上考虑二元函数

f(x，y)=3sinx+4siny+18sin(x+y)

的极值问题.由二元函数极值的必要条件， 得

(3)

(4)

整理得

(16t-9)(3t2+16t+9)=0.

(5)

对应t1有

对应t2有

又

那么

EG-F2=12sinxsiny+18sin(x+y)[3sinx+4siny].

受此启发，考虑一般的问题: 对于△ABC， 求xsinA+ysinB+zsinC的最大值. 为此，先给出著名的嵌入不等式.

引理1[2-4]对于任一△ABC和任意的实数x，y，z和正整数n， 均有

x2+y2+z2≥(-1)n+12(yzcos(nA)+zxcos(nB)+xycos(nC))，

(6)

当且仅当

x∶y∶z=sin(nA)∶sin(nB)∶sin(nC)

时不等式(6)取等号.

不等式(6)常称为Wolstenholme-Klamkin加权三角不等式.

定理1设x，y，z，k均是正数，且满足

对于任意三角形△ABC，有

(7)

其中上式等号成立当且仅当成立

(8)

在给出定理1证明之前， 先来证明一个引理.

则有

证由题设与正弦定理， 可知

a2∶b2∶c2=p(1-p)∶q(1-q)∶r(1-r)=p(q+r)∶q(p+r)∶r(p+q).

于是

sin(2A)∶sin(2B)∶sin(2C)

=(a2(b2+c2-a2))∶(b2(c2+a2-b2))∶(c2(a2+b2-c2))

=(2pqr(q+r))∶(2pqr(r+p))∶(2pqr(p+q)

=(q+r)∶(r+p)∶(p+q)

定理1的证明首先， 注意到对于给定的正数x，y，z， 满足

的k是唯一存在的. 由引理1， 可得

x2+y2+z2+2yzcos(2A)+2zxcos(2B)+2xycos(2C)≥0，x，y，z>0.

等号成立的条件是

x∶y∶z=sin(2A)∶sin(2B)∶sin(2C).

再利用二倍角公式有

(9)

用x2+k，y2+k，z2+k，k>0来代替上式中x，y，z， 则有

(x2+k)sin2A+(y2+k)sin2B+(z2+k)sin2C

上式等号成立的条件是

另一方面， 利用Cauchy-Schwarz不等式有

(xsinA+ysinB+zsinC)2

其中上式等号成立当且仅当

因此， 得到

即为

根据引理1知等号成立当且仅当

显然， 当x=3，y=4，z=18时， 由条件

可推出k=96， 故有

另一方面， 知道3sinA+4sinB+18sinC取极值时， 有

接着自然会思考一个问题，如何求解对应的余弦的线性组合的最大值问题， 如求xcosA+ycosB+zcosC 的最值问题. 为了简单起见，不妨设△ABC是锐角三角形， x，y，z都是正数的情形， 故得到如下结论[5-7].

推论1设x，y，z为任意给定的正数， 则对于任一△ABC， 有

(10)

该定理的证明可直接由嵌入不等式得到[5]. 接下来考虑(sinA)x·(sinB)y·(sinC)z与(cosA)x·(cosB)y·(cosC)z的上界问题.

定理2设x，y，z是任意给定的正数， 对于任意三角形△ABC， 有

(11)

其中不等式成立当且仅当

证对于任意给定的正数x，y，z， 令

对u，v，w应用不等式(10)式， 得

再利用加权幂平均不等式[8]， 得

即

所以

上式取等号当且仅当

定理3在锐角三角形△ABC中， 设x，y，z是任意给定的正实数， 则有

(12)

其中不等式取等号当且仅当

证利用推论1， 即在(10)式的x，y，z分别置换成

即有

然后， 利用加权幂平均不等式得

从而证得

[参考文献]

[1]徐利治.数学分析的方法及例题选讲-分析学的思想、方法与技巧[M].大连∶大连理工大学出版社.2007.

[2]Wu S， Debnath L. Generalization of the Wolstenholme cyclic inequality and its application[J]. Computers Mathematics with Applications January， 2007， 53: 104-114.

[3]Wolstenholme J. A book of Mathematical Problems[M]. London: Cambridge Press， 1867: 250-257.

[4]匡继昌.常用不等式[M].济南:山东科学技术出版社， 2004.10.

[5]朱华伟.嵌入不等式-数学竞赛命题的一个宝藏[J].中等数学，2010， 1: 14-17.

[6]杨学枝.数学奥林匹克不等式研究[M].哈尔滨:哈尔滨工业大学出版社，2008:420-428.

[7]沈虎跃.高中数学竞赛专题讲座-三角函数[M].杭州: 浙江大学出版社， 2007.

[8]潘杰， 孟勇.关于一道数学竞赛试题[J].大学数学， 2013， 29(4): 103-105.

Solutions to a Question of the Chinese Universities Mathematics

Competitions and Its Generalization

WANGYong-xi1，WANGZe-wen1，LIUBing2，QIUShu-fang1

(1. College of Science， East China Institute of Technology， Nanchang 330013， China;

2. Nanchang Second Middle School， Nanchang 330038， China)

Abstract:This paper presents three methods are presented for solving a question of the Chinese universities mathematics competitions， and studies the maximization of the linear summation of three interior angles’ sines of a triangle which extends the conclusion of the competition question. Finally， the bounded problems of the products of the sines and cosines exponents of three interior angles are studied.

Key words: universities mathematics competitions; triangle; embedding inequality; sine theorem; cosine theorem