环F2+uF2+u2F2上循环码的Gray距离

环F2+uF2+u2F2上循环码的Gray距离

张昊

(合肥工业大学数学学院，合肥230009)

[摘要]定义了环R=F2+uF2+u2F2(u3=0)到的一个新的Gray映射.首先介绍环R上奇长度的循环码的挠码，给出了各阶挠码的生成多项式.利用一阶挠码与二阶挠码确立了R上奇长度的循环码的Gray距离.

[关键词]循环码; 挠码; Gray映射

[收稿日期]2014-03-17

[中图分类号]O157.4[文献标识码]C

1引言

1994年Hammons，Sloane等人[1]发现Kerdock码等二元非线性码可以看作是Z4环上的循环码通过Gray映射得到的二元象，由此有限环上的纠错码理论研究有了突破性发展.此后，很多学者研究不同有限环上的循环码，常循环码，负循环码等线性码的结构[2-7]，并把这些码与域上的码利用Gray映射做出对应，从而发现很多性质良好的码，文献[2]给出了Z4上负循环码及Gray象的性质.多项式剩余环作为一种结构介于环和域之间的有限环，近年来其上纠错码理论也有很大的进展.文献[3]研究了环F2+uF2上常循环码及其Gray象的性质，文献[4]研究了Fq+uFq+…+uk-1Fq上重根常循环码的Gray象.文献[5]分类了Fpm+uFpm上长度为ps所有常循环码.

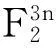
2基本概念

对于一个有限环R，考虑R的n元组集合Rn.Rn中的子集C称为R上长度为n的线性码，如果它是Rn的R-子模.R上长为n的线性码C称为循环码，如果它的每一个码字x=(x0，x1，…，xn-1)∈C，那么它的循环移位(xn-1，x0，…，xn-2)∈C. 含有8个元素的环

R={0，1，u，u2，1+u，1+u2，u+u2，1+u+u2}

可以表示为

F2+uF2+u2F2，

其中u3=0.环R实质上是多项式剩余类环F2[u]/(u3)，其中F2是二元域{0，1}.容易看出，环R是极大理想为的局部环，显然，R中的任意元素r可唯一表示为

r=r0+ur1+u2r2，

其中r0，r1，r2∈F2.

定义多项式映射

引理1与文献[5]中引理2.3类似

于是存在多项式e(x)∈R[x]，有

f1g1+f2g2=1+ue，

令e0=ue(1+ue)∈R[x]，有

e0(f1g1+f2g2)=ue，

于是

(1-e0)f1g1+(1-e0)f2g2=1，

即f1，f2互素.必要性是显然的.

Hensel引理设f(x)是R[x]中首一多项式，若存在两两互素的不可约多项式g1(x)，…，gr(x)∈F2(x)，使得

那么在R[x]中存在唯一两两互素的首一基本不可约多项式f1(x)，…，fr(x)，使得

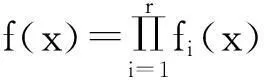
引理2如果xn-1=f1f2…fr是xn-1在F2[x]中两两互素的不可约分解，那么xn-1在R[x]中两两互素的首一基本不可约分解由xn-1=f1f2…fr直接给出.

证由于n是奇数，根据Hensel引理，xn-1在R[x]中可以唯一分解为两两互素的首一基本不可约多项式乘积.注意到F2[x]是R[x]的一个子环，由此得出结论.

3挠码

C(r)={c∈Rn|rc∈C}.

由验证易知，当C是R上循环码时，C(r)也是R上循环码.

引理3设C是R上长度为n的线性码，则有

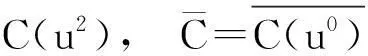
证由C(ui)定义及C=C(u0)知，对于c∈C，有uc∈C，所以有

C=C(u0)⊆C(u)⊆C(u2)，

因而也有

引理4设C是R上长为n的线性码，则

|C|=|Tor0(C)||Tor1(C)||Tor2(C)|..

证设码C具有下面标准形式的生成矩阵

其中Aij(i≥1，j≥1)是二元矩阵，则Tor0(C)=Res(C)的生成矩阵为

Tor1(C)的生成矩阵为

Tor1(C)的生成矩阵为

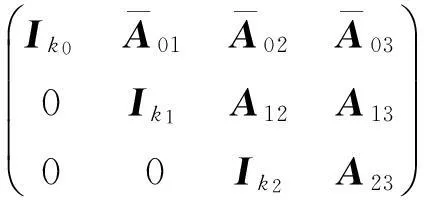
因为|C|=8k04k12k2，而

|Tor0(C)||Tor1(C)||Tor2(C)|=2k02k0+k12k0+k1+k2，

所以

|C|=|Tor0(C)||Tor1(C)||Tor2(C)|.

引理5[7]设C是R上奇长度n的循环码，则F2[x]中存在多项式g0，g1，g2满足

C=〈g0，ug1，u2g2〉，g2|g1|g0|(xn-1).

定理1设C=〈g0，ug1，u2g2〉是R上长为n的循环码，其中

g0，g1，g2∈F2[x]，g2|g1|g0|xn-1，

则Tori(C)(i=0，1，2)是长为n的二元循环码，生成多项式为gi(i=0，1，2).

证设

Ci=〈gi(x)〉⊆R[x]/〈xn-1〉，i=0，1，2，

对任意多项式f(x)∈Ci，存在α(x)∈R[x]/〈xn-1〉，使得

f(x)=α(x)gi(x)，

那么uif(x)=uiα(x)gi(x)∈C，从而有f(x)∈C(ui)，Ci⊆C(ui)，注意到

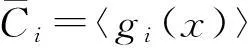
所以有〈gi(x)〉⊆Tori(C)⊆F2[x]/〈xn-1〉，由此得到|Tori(C)|≥2n-gi(x) ，从而有

|Tor0(C)||Tor1(C)||Tor2(C)|≥23n-deg(g0(x))-deg(g1(x))-deg(g2(x)) ，

而通过引理4和5得到了

|C|=|Tor0(C)||Tor1(C)||Tor2(C)|=23n-deg(g0(x))-deg(g1(x))-deg(g2(x)) ，

因而有

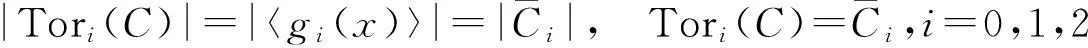
即证.

4Gray距离

Φ(r)=(c，c+a，c+b).

(r0，r1，…，rn-1)→(c0，c1，…，cn-1，c0+a0，c1+a1，…，cn-1+an-1，c0+b0，c1+b1，…，cn-1+bn-1)，

其中ri=ai+ubi+u2ci，i=0，…，n-1.

对R上任意元素r=a+ub+u2c，定义r的Gray重量

WG(r)=WH(Φ(ri))，

其中WH(Φ(ri))指的是Φ(ri)的Hamming重量.

对于R上码字c1和c2，两者的Gray距离

dG(c1，c2)=WG(c1-c2).

R上码C的Gray重量定义为其所有非零码字中的最小Gray重量，对于R上的线性码C，它的Gray距离dG(C)等于其最小Gray重量.

定理2设C=〈g0(x)，ug1(x)，u2g2(x)〉是R上奇长度为n的循环码，其中

g0(x)，g1(x)，g2(x)∈F2[x]，g2(x)|g1(x)|g0(x)|xn-1，

设d1，d2分别是Tor1(C)和Tor2(C)的Hamming距离，则

dG(C)=min{d1，3d2}.

证注意到二元域F2是R的子环，则gi(x)(i=0，1，2)可以看作R[x]/〈xn-1〉中元素，而

Tor0(C)⊆C，uTor1(C)⊆C，u2Tor2(C)⊆C，

则Tor0(C)，uTor1(C)，u2Tor2(C)都是C的子码，由Gray重量的定义，则Tor0(C)，uTor1(C)，u2Tor2(C)作为C的子码，其Gray距离分别为d0，d1，3d2.

所以C的Gray距离

dG(C)=min{d0，d1，3d2}，

而Tor0(C)⊆Tor1(C)，有d0≥d1，从而得出结论

dG(C)=min{d1，3d2}.

例1已知在F2[x]中，

x7-1=(x-1)(x3+x+1)(x3+x2+1).

设C=〈g0(x)，ug1(x)，u2g2(x)〉是F2+uF2+u2F2上长7的循环码，其中

g0(x)=x3+x+1，g1(x)=x3+x+1，g2(x)=1.

因为Tor0(C)=〈g0(x)〉是二元[7，4，3]-线性码，Tor1(C)=〈g1(x)〉是二元[7，4，3]-线性码，而Tor2(C)=〈g2(x)〉是二元[7，7，1]-线性码，根据定理2，码C是F2+uF2+u2F2上(7，215，3)-线性码，它的Gray像是二元[21，15，3]-线性码.

5结束语

本文利用挠码确定了环F2+uF2+u2F2(u3=0)上奇长度的循环码的Gray距离，这为研究环F2+uF2+u2F2上编码与译码提供了重要的理论依据.进一步的研究是确立更一般的有限链环Fq+uFq+…+uk-1Fq(uk=0)上循环码的齐次距离.另外，如何利用环F2+uF2+u2F2上循环码构造参数较好的二元线性码也值得进一步探讨.

[参考文献]

[1]Hammons Jr A R， Kumar P V， Calderbank A R， et al. The Z4-linearity of Kerdock， Preparata， Goethals， and related codes [J]. IEEE Transactions on Information Theory， 1994， 40(2): 301-319.

[2]Wolfman J. Negacyclic and cyclic codes over Z4[J]. IEEE Transactions on Information Theory， 1999， 45(7): 2527-2532.

[3]Qian J F， Zhang L N， Zhu S X. (1+u)constacyclic and cyclic codes overF2+uF2[J]. Applied Mathematics Letters， 2006， 19(8): 820-823.

[4]朱士信， 李平， 吴波. 环Fq+uFq+…+uk-1Fq上一类重根常循环码[J]. 电子与信息学报， 2008， 30(6): 1394-1396.

[5]Dinh H Q， Nguyen H D T. On some classes of constacyclic codes over polynomial residue rings [J]. Advances in Mathematics of Communications， 2012， 6(2)：175-191.

[6]Bonnecaze A， Udaya P. Cyclic codes and self-dual codes over F2+uF2[J]. IEEE Transactions on Information Theory， 1999， 45(4): 1250-1255.

[7]Dinh H Q， López-Permouth S R， Cyclic and negacyclic codes over finite chain rings [J]. IEEE Transactions on Information Theory， 2004， 50(8): 1728-1744.

Gray Distance of Cyclic Codes Over F2+uF2+u2F2

ZHANGHao

(School of Mathematics， Hefei University of Technology， Hefei 230009， China)

Key words: cyclic code; torsion code; Gray distance