研究生数学公共课程中教学案例创新与建设的思考

研究生数学公共课程中教学案例创新与建设的思考

张玲玲1，2，黄建华2，黄立宏1

(1. 湖南女子学院信息技术系，长沙410004;2. 国防科技大学理学院，长沙410073)

[摘要]通过对磁浮列车悬浮系统的Hopf分支的研究，提出了任课教师将科学研究中的实际问题抽象出来，按照“发现问题、分析问题、解决问题、总结验证”研究过程，“驱动的问题背景、问题的数学描述、所需数学知识、数学推导与证明、数值仿真验证、回归原始问题解释和分析”的步骤，将科研成果转化为精彩教学案例，启发学生通过实际问题的数学分析与处理，激发其活学活用数学兴趣、提高创新能力.

[关键词]研究型案例； 创新能力； 教学案例创新

[收稿日期]2014-11-15

[基金项目]国防科技大学研究生数学公共课一流课程体系建设项目

[中图分类号]O175.17;G642[文献标识码]C

1引言

在教学中，我们要求研究生注重理论学科知识的融合和交叉，打牢数学基础，强化创新能力.为了调动工科研究生学习数学课程的兴趣，培养他们研究式、自主式学习的能力，达到更好的教学效果，结合研究生数学公共课程中常微分方程的定性理论和数学建模课程，我们将科研中的抑制磁悬浮列车振动问题转化为教学案例.

磁浮列车是利用电磁吸力或斥力悬浮和导向车体的一种新型交通工具， 它具有速度快、噪音低、振动小、运营和维护费用低、安全环保等优点，因此德国、日本、英国、美国、韩国、中国等许多国家纷纷开展了磁浮列车技术的研究.虽然磁悬浮技术已经经历了数十年的发展，但相对于其他技术成熟的陆地交通工具来说，仍然存在一些需要深入研究的问题， 如车轨耦合共振问题等.

车轨耦合振动是磁悬浮技术中的一个技术难题，目前常用的抑制车轨耦合振动的方法是增加磁浮列车轨道质量和提高轨道刚度，以此来降低振动发生的可能性.但是这种方法造价太高，不利于磁浮技术的推广.因此有许多学者开始从非线性动力学角度来阐述车轨振动的成因，试图找到控制车轨振动的有效方法.时滞的存在和反馈参数的变动都会导致系统的动力学行为发生改变，如出现混沌、分支等.Hopf分支产生的极限环与振荡现象密切相关，因此讨论时滞和反馈控制参数变动引起磁悬浮系统的Hopf分支现象，对研究磁悬浮系统车轨振动的问题有着重要的理论指导意义.

对具有时滞状态反馈控制的磁悬浮系统进行稳定性分析，得到影响系统稳定性的时滞和速度反馈控制增益的变化关系.并在时滞固定的情况下，采用多尺度方法计算了周期解的近似表达式，得出控制参数取值在一定范围内系统保持稳定，变化控制参数可以产生两个极限环，并可能产生双Hopf分支，从而导致磁浮列车的振动.

2问题的数学描述

将数学建模的思想与磁浮列车悬浮系统相结合，建立模型.刚性轨道条件下，磁浮列车单电磁铁-轨道悬浮控制系统的结构示意图如图1所示：

图1　磁浮列车悬浮系统结构示意图

其中，Mg和F(i，z)表示电磁铁的重量和电磁力，z(t)代表电磁铁在垂直方向上的位移，变量i(t)和v(t)分别表示电磁铁线圈的电流和电压.系统的动力学和电磁力方程为

(1)

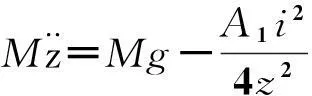
(2)

其中A1=N2μ0S0，μ0为磁导强度，N是线圈匝数，S0和r是电磁铁的极面积和电阻，从方程(2)中，得到

并将其代入方程(1)可得

控制电压

各个状态在平衡点位置的取值分别为

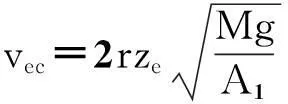
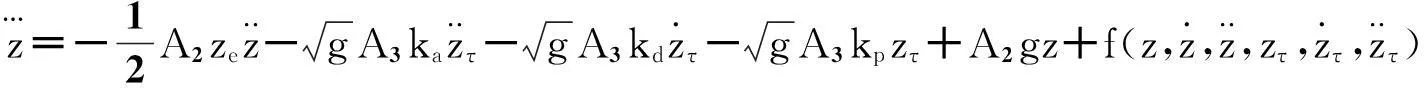
(3)

方程(3)的线性系统的特征方程为

D(λ，τ)=λ3+aλ2+bλ2e-λτ+cλe-λτ+de-λτ+e=0，

(4)

接下来，将通过常微分方程定性理论对特征方程(4)的研究，分析控制参数kd和时滞参数τ对系统动力学行为的影响.

3稳定性分析和多尺度计算

设±iβ为特征方程(4)的一组纯虚根，β代表振动频率.进行稳定性分析，可以得到控制参数kd和时滞参数τ的临界值分别为

(5)

(6)

选取系统参数

N=320，r=0.5Ω，M=500kg，μ0=4π×10-7，ze=0.008m，S0=0.047m2，

以及几组不同的位置和加速度控制参数kp和ka， 可以得到在kd，τ参数平面上由方程(5)，(6)确定的稳定区域的边界曲线，它们的形状都是类似的，如图2所示：

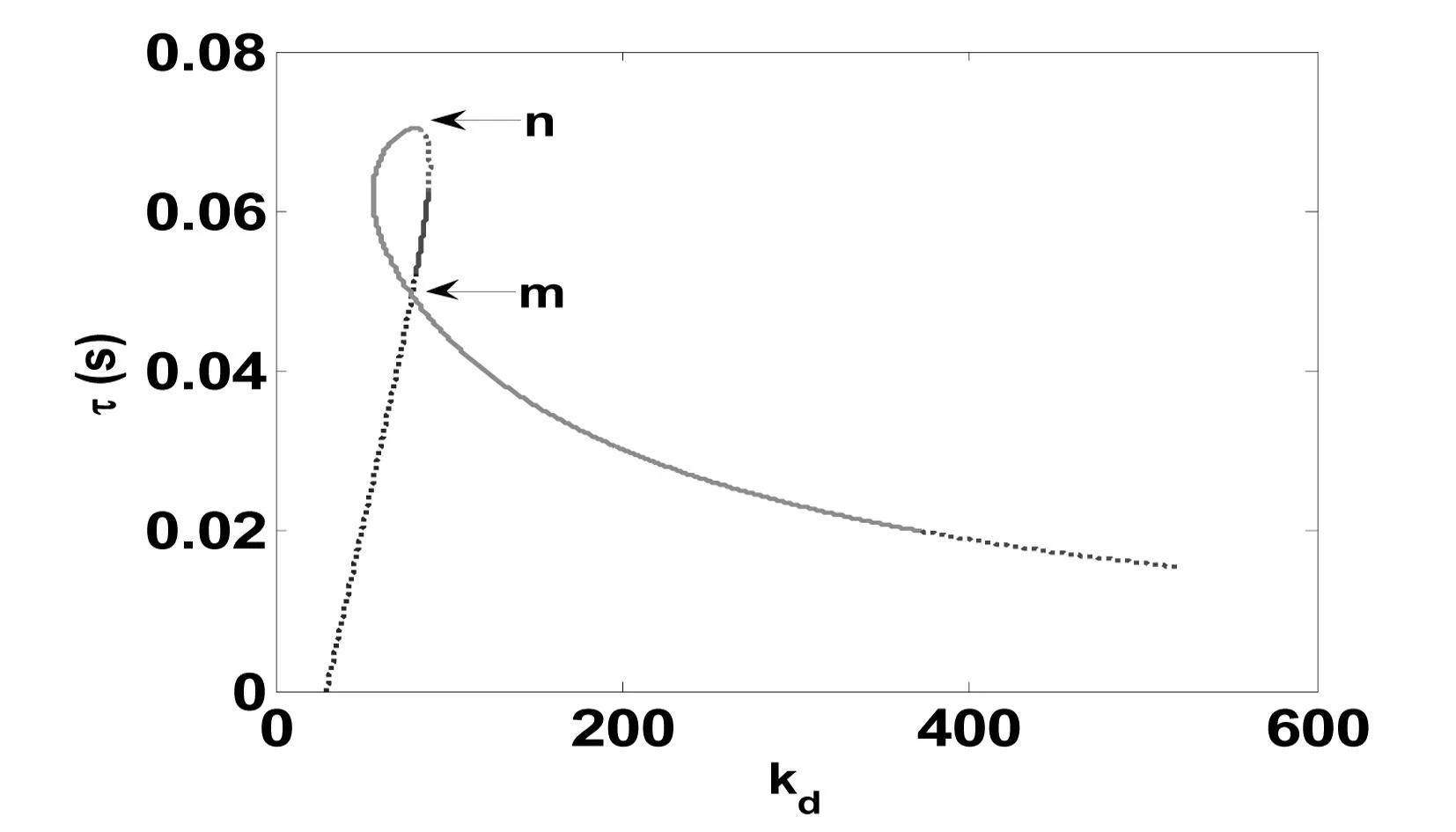
(a) k a=8　　　　　　　　　　　　　　　　 (b) k p=2000 图2　在k d，τ平面上的稳定区域和分支曲线

通过验证Hopf分支的穿越条件，得到除顶点n外，曲线上每个点都是Hopf分支点，在交点m，有可能发生双Hopf分支.

根据常微分方程定性理论知识，接下来用多尺度的方法计算Hopf分支引起的周期解的近似表达式，并分析分支的类型.引入小参数ε和去谐参数δ来描述分支临界值kd0附近的参数kd，即

kd=kd0+ε2δ.

可以得到方程的周期解近似表达式为

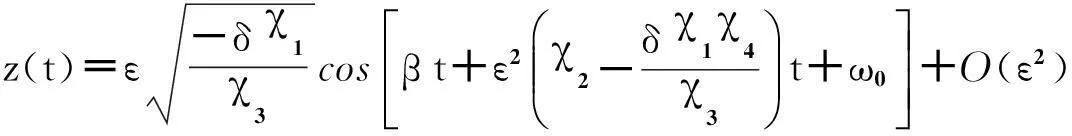
参考文献其中χ1，χ2，χ3和χ4的表达式可以[1]，此处省略.

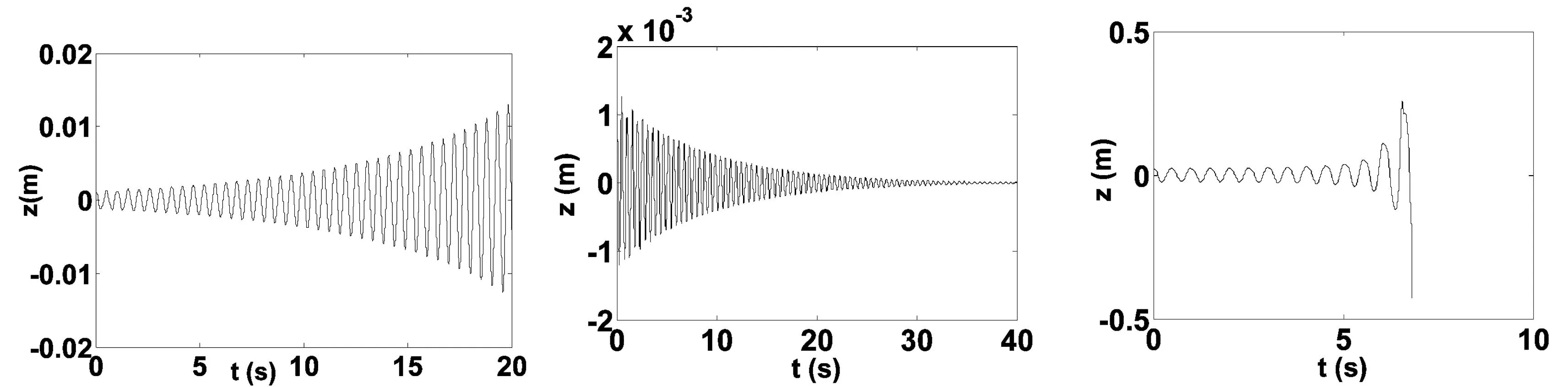
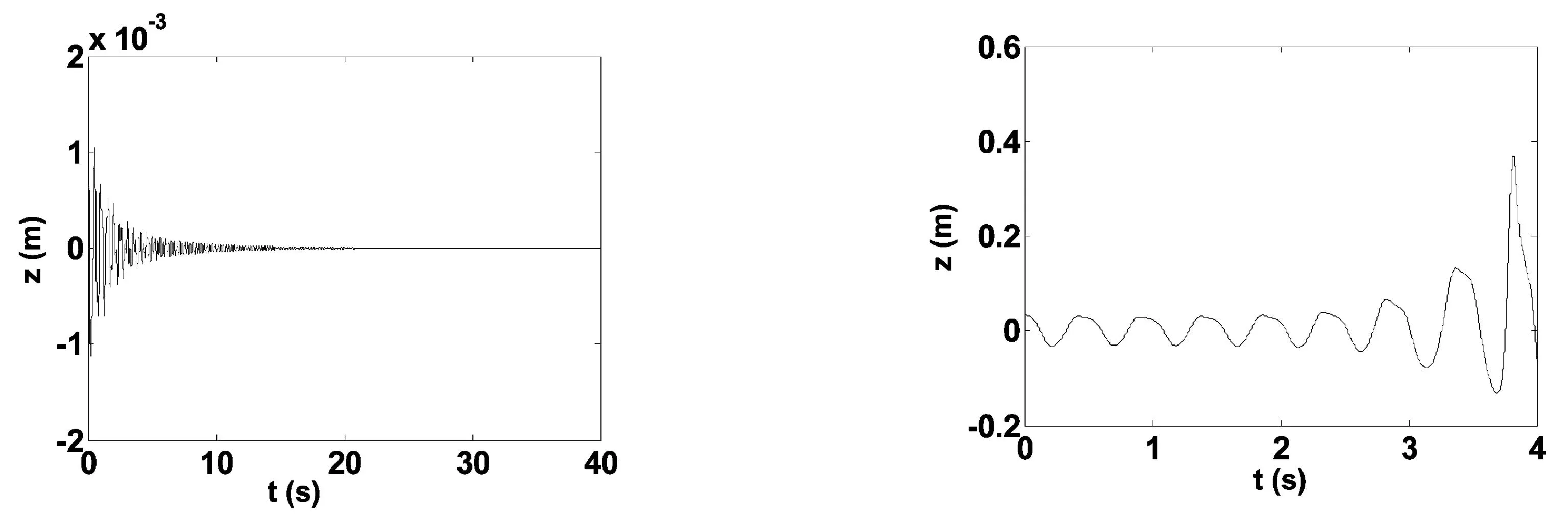
若χ1和χ3的符号相同，当δ<0，也即kd

χ1<0，χ3<0(χ1>0，χ3>0)

时，极限环是稳定的(不稳定的)，且Hopf分支是超临界的(亚临界的).

图3　分支曲线 (实线表示χ 3<0，虚线表明χ 3>0)

若χ1和χ3的符号不相同，当δ>0，也即kd>kd0，极限环存在.当

χ1>0，χ3<0(χ1<0，χ3>0)

时， 极限环是稳定的(不稳定的)，且Hopf分支是超临界的(亚临界的).

接下来，根据上面的结论对一组具体的控制参数来判定Hopf分支的性质.由图2，对每一个固定时滞τ，系统有两个不同的速度控制参数的临界值，kd10.

由上述讨论， Hopf分支的性质和极限环的稳定性由χ3的符号决定.选取kp=2000和ka=10，对相应的Hopf分支曲线上每点的χ3符号进行计算，得到结果如图3所示.

4数值仿真验证

同样地，选取控制参数kp=2000，ka=10.由图2(b)，在交点m，(kd0，τ0)≈(78，0.049).

当时滞τ>0.049s时，磁悬浮系统是不稳定的，因此只考虑时滞小于0.049s的情形.选取τ=0.047s作为例子，由图3，可以得到两个速度反馈增益临界值

kd1=76.61，kd2=87.75，

即Hopf分支在kd1点是亚临界的，在kd2点是超临界的.接下来，将对上述理论结果与数值仿真进行比较.

如果kd=75≤kd1=76.61，平凡解是发散的，也即不稳定的(图4(a));

若kd=78>76.61和初始条件z0=0.001m，运动轨迹趋向于平凡解，表明它是渐近稳定的(图4(b)).但是，如果选取kd=78和一个较大的初始条件z0=0.022m，运动轨迹开始发散 (图4.4(c))，表明当kd>76.61时出现一个不稳定的极限环， Hopf 分支是亚临界的.

(a) k d=75，z 0=0.001m (b) k d=78，z 0=0.001m(c) k d=78，z 0=0.022m　　 图4　不同的k d和初始条件下， 状态z的运动轨迹

由图5(a)，若kd=8587.75，平凡解是不稳定的并出现一个稳定的极限环，这表明Hopf分支是超临界的;如果选取相同的控制参数kd=90，不同的初始条件z0=0.033m(大于图5(b)中的初始条件)，得到的解迅速增大(图5(d))，这表明当kd>87.75时同时存在着不稳定的极限环.

(a) k d=85，z 0=0.001m　　　　　　　　　　 (b) k d=85，z 0=0.0328m

(c) k d=90，z 0=0.001m　　　　　　　　　　　　　(d) k d=90，z 0=0.033m 图5　不同的k d和初始条件下， 状态z的运动轨迹

因此，这些仿真结果与理论分析出的局部分支图(图3)非常吻合.同时表明在平衡点稳定的参数区域(kd1，kd2)内，kd=kd1时发生的亚临界分支所导致的不稳定极限环将一直存在.

5结论

没有科研的教学不是高水平的教学.联系教学实际搞科研，通过科研切实提高教学质量.将科研成果和学术思想融入到教学环节中，激发学生的学习兴趣，不断提高教学绩效和教学质量，是我们研究生数学课程建设的思想.

工科研究生的数学基础薄弱，对所学的数学基础知识重视不够、掌握不扎实，导致其缺乏运用数学思想和方法解决专业问题的能力，影响其从事深层次专业研究的创新能力.因此我们采用案例式教学，将工科中遇到的科研问题与数学知识结合起来，调动他们学习数学课程的兴趣，培养他们研究式、自主式学习的能力.

本文结合数学建模和常微分方程定性理论的知识，讨论了时滞状态反馈的磁浮列车悬浮系统的稳定性和Hopf分支.首先描述了使系统保持稳定的时滞和速度反馈增益的取值.接下来， 给出了速度控制增益与Hopf分支的关系.计算了周期解的近似表达式，并用数值仿真验证了理论结果.这些理论分析和数值仿真可以应用到样车试验中，从而为抑制车轨振动提供理论指导作用.在位置和加速度反馈增益确定的前提条件下，适当控制反馈时滞和调节速度反馈增益，可以保证悬浮系统的稳定性，同时应该避免过大的外部干扰，否则由于亚临界Hopf分支的存在，将会使原本应该稳定悬浮的列车出现剧烈振动.

[参考文献]

[1]张玲玲. 磁浮列车悬浮系统的Hopf分岔及滑模控制研究[D].湖南大学博士学位论文， 2010.

[2]黄建华，李建平. 研究生数学课程体系优化和教学模式创新的研究与实践，军队院校数学课程创新教学研讨会论文集(上册)[M].北京：国防工业出版社，2011.

[3]李超，屈龙江，戴清平. 研究生数学公共课程体系建设[J].高等教育研究学报，2013，36(S1)：38-41.

Reflections on the Teaching Case Innovation and the Construction

of Mathematic Public Teaching for Postgraduates

ZHANGLing-ling1，2，HUANGJian-hua2，HUANGLi-hong1

(1. Department of Information and Technology， Hunan Women′s University， Changsha 410004， China;

2. College of Science， National University of Defense Technology， Changsha 410073， China)

Abstract:Through the study on the Hopf bifurcation of maglev system， the authors proposes a teaching reform pattern， some practical problems from scientific research were selected for this course. The teaching was conducted in four stages， i.e.， the problem finding， problem analysis and modeling， problem solving， the research process summarizing. Four steps are provided such as the problem background， the required mathematical knowledge， mathematical derivation and proof， numerical simulation and application to the original question. Some research results are selected to be the good teaching case to improve the ability of innovation of the postgraduates.

Key words: research of case; the ability of innovation; teaching case innovation