多项式环中单项式理想的分解

多项式环中单项式理想的分解

唐慧，吴汉捷，褚利忠

(苏州大学数学科学学院，江苏苏州215006)

[摘要]利用单项式理想生成元的性质，给出了一类特殊单项式理想(生成元是变量的纯幂)的幂的分解表达式，这不仅拓宽了我们对多项式理论内容的认识，而且这样的分解表达式提供了这类单项式理想正则度(Castelnuovo-Mumford regularity) 计算的方法.

[关键词]多项式环； 单项式理想； 单项式理想的分解

[收稿日期]2013-11-30;[修改日期]2015-04-17

[基金项目]苏州大学大学生创新创业训练计划；国家自然科学基金(11201326)

[中图分类号]O153.3[文献标识码]A

抽象代数是数学专业的重要课程， 而多项式环是抽象代数里重要的知识点. 本文通过对某些特殊单项式理想分解的讨论，加深了对多项式理论内容的理解，更为有意义的是，本文中给出的这类特殊单项式理想的分解提供了这类理想正则度(Castelnuovo-Mumford regularity)计算的方法(见[1]).

约定：在本文中，约定K是一个数域.

定义1[2]设I⊆R=K[x1，x2，…，xn]是一个理想，如果I是由单项式生成的，则称I是多项式环R的单项式理想.

下面两个结果在文献[3]习题中出现过.

引理1设K是一个数域，I1，I2，I3为多项式环K[x1，x2，…，xn]的单项式理想，则有

I1∩(I2+I3)=I1∩I2+I1∩I3.

引理2设u1，u2，…，um为多项式环K[x1，x2，…，xn]的单项式理想，其中u1=ab，a，b为单项式，且(a，b)=1，则有

(ab，u2，…，um)=(a，u2，…，um)∩(b，u2，…，um).

定义2[2]如果单项式理想I可写成表示式：

定理1[2]令I⊆K[x1，x2，…，xn]是一个单项式理想，则存在I的一个不可约分解：

定理2[2]设I⊆K[x1，x2，…，xn]是一个单项式理想，则I的一个不可约分解

中出现的Qi(i=1，2，…，m)构成的集合由I所唯一确定的.

引理3设I，J⊆K[x1，x2，…，xn]是单项式理想，且理想I的极小生成元集的每一个生成元中都不出现x1，则

其中α1≥1.

证设I=(u1，u2，…，um)，且(x1，ui)=1，i=1，2，…，n. 则

于是， 由引理2可得

假设当r=k时，

由归纳假设得

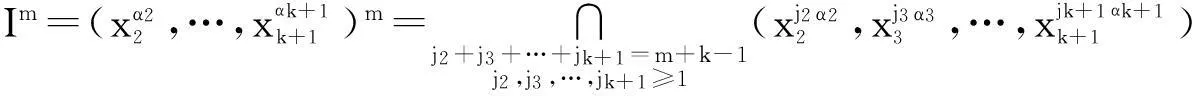
将前面的m换成t， t=1，2，…，m-1，于是

[参考文献]

[1]Bermejo I， Gimenez P. Saturation and Castelnuovo-Mumford regularity [J]. Journal of Algebra， 2006，303(2): 592-617.

[2]Herzog J， Hibi， T. Monomial Ideals [M]. London: Springer London Ltd， 2011.

[3]Bruns W， Herzog J. Cohen-Macaulay Rings [M]. New York: Cambridge University Press， 1998.

Monomial Ideal Decomposition in a Polynomial Ring

TANGHui，WUHan-jie，CHULi-zhong

(Department of Mathematics， Soochow University， Suzhou Jiangsu 215006， China)

Abstract:The monomial ideal decomposition of the power of a particular monomial ideal (its generators is pure powers of the variables) is given by some properties of generators of a monomial ideal. This study widen our scope of knowledge to the theory of a polynomial ring and help us compute the Castelnuovo-Mumford regularity of this kind of monomial ideal.

Key words: polynomial ring； monomial ideal； monomial ideal decomposition