数列{sinnk}发散的证明
数列{sinnk}发散的证明
焦红英,刘卫江,梁放驰
(空军工程大学理学院,西安710051)
[摘要]研究了当k是正整数时,数列{sinnk}的敛散性,文献[1]给出了{sinn}和{sinn2}发散的证明,但是证明方法复杂,不便阅读.为此,本文进行了两个方面的研究:一方面是运用简单的方法证明了{sinn}和{sinn2}的发散;另一方面证明了一个重要结论,即{sinnk}发散.
[关键词]数列; 敛散性; 极限
[收稿日期]2014-12-29;[修改日期]2015-02-28
[基金项目]国家自然科学基金(1107125); 国家级大学生创新训练项目(201490052045)
[中图分类号]O174.3[文献标识码]C
1引言
关于数列{sinnk}的敛散性,当k是正整数时,文献[1]对此作了讨论.对于k≥3的情形作者猜想{sinnk}发散,而对k=1和k=2的情形,作者给出了{sinn}和{sinn2}发散的证明,不过证明方法比较复杂,似乎不太适合广泛的学习阅读.以下本文给出一种比较简单的证明数列{sinn}和{sinn2}发散的方法,并同时给出k≥3时,{sinnk}发散的证明.
2主要结论
首先,利用三角函数公式,容易证明以下结论: ∀x,y∈
sin2y=sin2(x+y)-sinx·sin(x+2y),
(1)
sin2y=cos2(x+y)-cosx·cos(x+2y).
(2)
定理1如果sinp≠0,则数列{sin(pn+q)},{cos(pn+q)}发散;如果sin(48a)≠0,则{sin(an2+b)},{cos(an2+b)}发散.
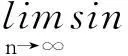
sin2p =sin2(p(n+1)+q)-sin(pn+q)·sin(pn+q+2p)
=sin2(p(n+1)+q)-sin(pn+q)·sin(p(n+2)+q).
(3)
若令n→∞,则有sin2p=A2-A·A=0 矛盾.
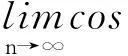
sin2p =cos2(p(n+1)+q)-cos(pn+q)·cos(pn+q+2p)
=cos2(p(n+1)+q)-cos(pn+q)·cos(p(n+2)+q).
(4)
若令n→∞,则有sin2p=B2-B·B=0 矛盾.
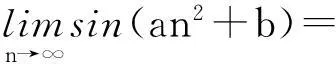
sin2(24an2) =sin2(an2+b+24an2)-sin(an2+b)·sin(an2+b+48an2)
=sin2(a(5n)2+b)-sin(an2+b)·sin(a(7n)2+b).
(5)
若令n→∞,则有sin2(24an2)=C2-C·C=0.
即
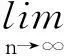
再由
sin(24a(n+1)2-24an2)=sin(48an+24a)
=sin(24a(n+1)2)cos(24an2)-cos(24a(n+1)2)sin(24an2).
(6)
注意到{cos(24an2)}及{cos(24a(n+1)2)}有界.令n→∞,则有
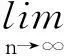
又
sin(48a)=sin[48a(n+1)+24a-(48an+24a)]
=sin[48a(n+1)+24a]cos(48an+24a)-cos[48a(n+1)+24a]sin(48an+24a).
(7)
注意到{cos(48an+24a)}及{cos(48a(n+1)+24a)}有界.再令n→∞,则有sin48a=0矛盾.所以, {sin(an2+b)}发散.
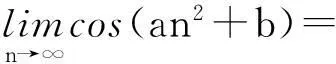
sin2(24an2) =cos2(an2+b+24an2)-cos(an2+b)·cos(an2+b+48an2)
=cos2(a(5n)2+b)-cos(an2+b)·cos(a(7n)2+b).
(8)
若令n→∞,则有sin2(24an2)=D2-D·D=0.即
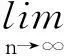
再由
sin(24a(n+1)2-24an2)=sin(48an+24a)
=sin(24a(n+1)2)cos(24an2)-cos(24a(n+1)2)sin(24an2).
(9)
注意到{cos(24an2)}及{cos(24a(n+1)2)}有界.令n→∞,有
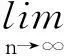
又
sin(48a) =sin[48a(n+1)+24a-(48an+24a)]
=sin[48a(n+1)+24a]cos(48an+24a)-cos[48a(n+1)+24a]sin(48an+24a).
(10)
注意到{cos(48an+24a)}及{cos(48a(n+1)+24a)}有界.再令n→∞,则有sin48a=0矛盾.所以,{cos(an2+b)}发散.
通过定理1证明,很容易得到以下两个推论:
推论1定理1中,若p=1,q=0,则数列{sinn},{cosn}发散.
推论2定理1中,若a=1,b=0,则数列{sinn2},{cosn2} 发散.
为了进一步证明对任意的正整数k,数列{sinnk} 发散,还需要两个引理作为铺垫.
引理1设k为正整数,则存在整系数多项式f(x),使得
sin(2kx)=cosx·f(sinx).
这个结论只要反复利用正弦的倍角公式,即可证明.
引理2设ψ(x)是次数不低于1的整系数多项式,则数列{sinψ(n)}不可能以零为极限.
证对ψ(x)的次数使用归纳法.
当k=1时,ψ(x)=px+q,其中p,q 为整数.由定理1可知{sinψ(n)}发散.所以,k=1时命题成立.
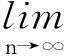
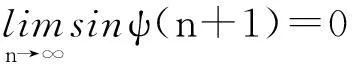
而
sin[ψ(n+1)-ψ(n)]=sin(ψ(n+1))cos(ψ(n))-cos(ψ(n+1))sin(ψ(n)).
故
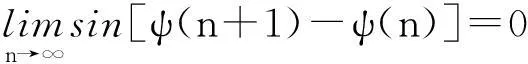
但ψ(x+1)-ψ(x)是k次多项式,由归纳假设
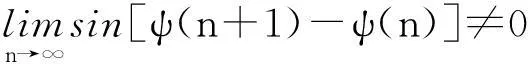
矛盾.所以,命题对k+1亦成立.
定理2设k为正整数,则数列{sinnk}发散.
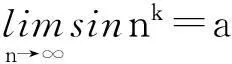
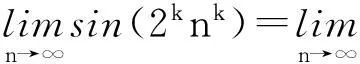
由引理1知,存在整系数多项式f(x),使得
sin(2k·nk)=cos(nk)f(sinnk).
由f(x)的连续性可知
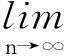
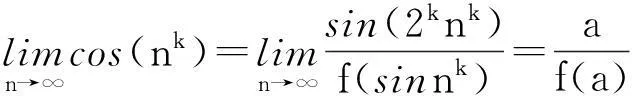
sin[(n+1)k-nk]=sin(n+1)kcosnk-cos(n+1)ksinnk.
令n→∞,有
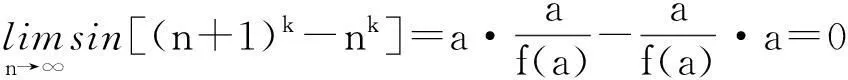
但ψ(x)=(x+1)k-xk是k-1次多项式,所以当k>1时与引理2的结论矛盾.
当k=1时,
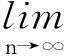
同样矛盾.
综上所述,当k是正整数时,{sinnk}发散.
[参考文献]
[1]舒阳春.高等数学中的若干问题解析[M].北京:科学出版社,2006.
[2]李文荣.分析中的问题研究[M].北京:中国工人出版社,2001.
[3]钱昌本.高等数学解题过程中的分析和研究[M].北京:科学出版社,1999.
[4]侯云畅,冯有前,刘卫江.高等数学[M].北京:高等教育出版社,2000.
Proof of Sequence {sinnk} Divergence
JIAOHong-ying,LIUWei-jiang,LIANGFang-chi
(Science of College, Air Force Engineering University, Xi’an 710051, China)
Abstract:When k is a positive integer, the sequence {sinnk} of convergence and divergence of the literature [1] only gives {sinn} and {sinn2} diverge proof, but proof complexity, inconvenience read. In this paper, we studied two aspects: on the one hand is the use of a simple method proof {sinn} and {sinn2} divergence; On the other hand proved an important conclusion that {sinnk} diverge.
Key words: sequence; convergence and divergence; limit

