职高学生数学运算错误的分析探究

□浙江省宁波市东钱湖旅游学校 周红

职高学生数学运算错误的分析探究

□浙江省宁波市东钱湖旅游学校 周红

数学运算错误无所不在，形态各异。文章从正确选用公式、有效利用条件、整体把握思路、严谨运用概念、瞄准求解目标、学会验算技巧等六方面对职高学生数学运算错误作了详细分析指导；系统地分析错误，合理归类，逐个击破，希望学生从有意识地少犯错误，到自动化地修正错误，多体验成功的喜悦，从而达到乐学会学的成效。

职高数学 运算 错误 分析 解决

在近些年的高三数学教学中，我发现学生的数学运算能力越来越差；有幸会做，也要不幸算错。表象似乎是中考使用计算器带来的数据处理技能低下，但究其原因，我发现还有许多深层影响因素。

运算能力是包括分析运算条件、研究运算方向、选择运算公式、确定运算程序等一系列过程的思维能力，也包括在实施运算过程中遇到障碍而调整运算的能力，以及实施运算和计算的技能。可见，运算除了是对数据、公式的求解，还有对数据的处理分析，以及对运算方法和程序的正确选择。分析数学运算错误的原因势必成为提高数学运算能力的必要途径。

一、未能正确选用运算法则和计算公式

数学运算要求正确使用各种运算法则，包括不等式、集合、函数、向量、方幂、指数、对数、三角、数列、排列组合二项式等各个方面的运算法则和计算公式。此外还有几何内容的各种计算公式。学生对这些法则和公式的使用常有误用和错用的情况发生。

错因分析：k1k2=-1的确是判断两直线是否垂直的条件之一，但这个条件的前提是两直线的斜率必须存在。本题中这个前提条件不一定成立，故选用k1k2=-1求m导致漏根。基于此分析，正确选用直线方程一般式判断垂直的条件：A1A2+B1B2=0。

二、对已知条件不会有效利用，缺乏各种简化计算的技能

【例2】等差数列｛an｝，a1=500，公差d=-30，求Sn的最大值。

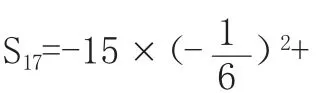
解题分析：一元二次函数配方求最值往往是学生解此题的定向思维，但这种机械方法在此题中显得运算复杂：配方引起数据庞大，容易引起运算错误，结论的导出危机重重（除却计算难度，n∈N*也是学生常漏的隐形条件，而n=17还是n=18时Sn有最大值也是学生易纠结弄错的关键点）。

另辟蹊径的解题分析：整体把握该数列特点：a1=500，公差d=-30，首项为正的递减数列，求前n和的最大值即求所有正数项之和。

简解：an=500+(n-1)×（-30）=530-30n，

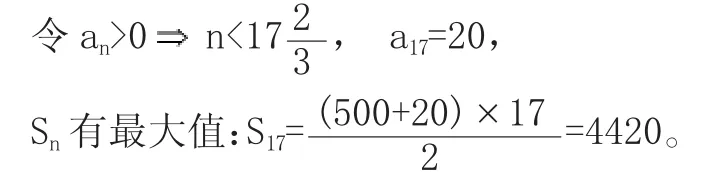
三、列式混乱，欠缺条理，解题思路不清

【例3】：已知△ABC三个顶点A(5，1)，B(-1，2)，C(1，-3)，求△ABC的外接圆方程。

解：设圆的一般方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)

分析：以上解法是高三升大班一位数学程度中上的学生板演过程，很遗憾，尽管她很努力地去创建二元一次方程组，但过程中一次“小小的漏乘”，最终使她功亏一篑，远离了正确答案，正所谓“失之毫厘，差之千里”。与这位程度中上学生相似，在一次模拟考中全班竟有一半学生在列出三元方程组后无从下手，放弃解答。全班46个学生最终得出正确答案的竟只有3位！

除了计算能力薄弱之外，最重要原因是学生解方程组缺乏层次性和条理性，导致列式凌乱，交代不清，将算式胡乱迭代穿插，频频失误，导致半途而废。一般说来，当未知元较多、方程个数较多时，宜对式子加以编号，对式子变形或变换前，先作整体统筹规划，明确解答过程中各式的因果关系，切忌迷失方向，瞎撞乱碰。

思路分析：第一步：用加减消元法消去F（因为三个方程中F的系数均为1，消F要比学生板演时消D简单得多，这是对三个方程先作整体思考而得出的正确判断，学生之所以没想到，不是因为想不到，而是有拿来就做的坏习惯，给自己一分钟的思考时间条理就会清楚许多；二式相减时，注意同类项配对相减，可简化计算，减少错误的发生率）；第二步：解关于D,E的二元一次方程组，则水到渠成。

四、推理说明欠周全，甚至逻辑混乱

【例4】bn=32n，求数列｛bn｝的前n项和。

学生解答：b1=9，b2=81，b3=729，｛bn｝是等比数列，q=9，

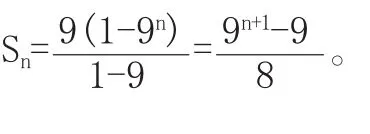
分析：答案虽然是对的，但纵视解答过程，通过前三项就说明｛bn｝由特殊推出一般结论，犯了说理不足、逻辑推理不严密的问题。

∴｛bn｝是等比数列，q=9，b1=32=9，

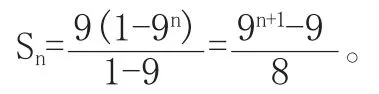
五、审题欠慎，概念模糊，弄错解答目标

【例5】某班要从五名运动员中选四名参加4×100米接力跑，其中甲必须跑第一棒，乙不能跑第四棒，问共有多少种不同排法种数。

错误分析：学生的解法思路很简单，按限制对象分二步：第一步先排乙，有2种排法；第二步从剩余3人中任选2人排另二个位置，有种排法，根据分步计数原理，共有=12种排法。

如此分析却与题意相违：乙不跑第四棒代表他一定被选中？题意是乙可以被选中也可以落选，但如果选中必不跑第四棒，显然审题出错，解答错误也无可避免。

正解：按限制位置分二步：第一步先排第四棒，有3种排法；第二步排第二和第三棒，有种排法，根据分步计数原理，有=18种排法。

六、变形或运算失误，欠缺估算和验算的技能，不能及时修正错误

【例6】已知数列｛an｝前n项和Sn=n2+2n+5，求an。

错解：n≥2时，an=Sn-Sn-1=n2+2n+5-（n-1）2+2(n-1)+5=6n+7，n=1时，a1=13与S1=8不符，

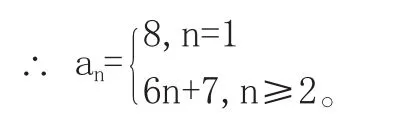
分析：显然，在二式相减时因缺乏整体思想，学生漏写了括号，导致结论错误。但是学生如果只需简单验算：a2=S2-S1=13-8=5与a2=6×2+7=19不符，就能察觉错误，及时修正。

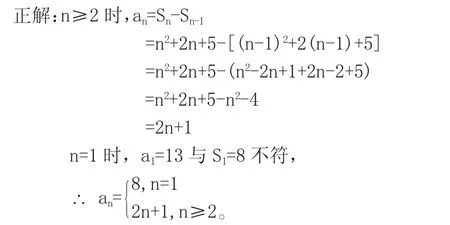
在数学运算中，犯错误的机会很多，需要学生的细心，更需要用心。为了尽可能地避免和防止犯错，培养数学运算能力，教师需要明确：掌握算理是培养运算能力的基础；重视口算是培养运算能力的关键；有效练习是培养运算能力的手段；养成良好的学习习惯更是培养运算能力的途径。运算能力的提高也将带来思维的创造性和应用性，在数学运算能力的提高中将逐渐系统地养成从事脑力劳动的习惯——计划自己的工作，寻找完成工作的合理途径，对结果进行批判评价。这也是提高数学运算能力的终极目标。