循循善诱，走出困境

□江苏省苏州市木渎金山高级中学 丁妍

循循善诱，走出困境

□江苏省苏州市木渎金山高级中学 丁妍

数学课堂上，学生在课堂解答时总会遇到这样或那样的困难，此时，就要求我们教师能做一个循循善诱的引导者，通过运用“启发式诱导”、“对比式诱导”、“转换式诱导”等多种诱导方法，去“牵”着学生向前走，去深入思考，去探索答案，从而使学生走出困境。

循循善诱 诱导方法 走出困境

数学课程标准中明确指出：“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。有效的数学学习不能单纯地依赖模仿和记忆，动手操作、自主探索、合作交流是学生学习数学的重要方式。”教师的职责主要不在于“教”，而在于引导学生“学”。课堂教学是学生获取知识信息、培养和提高思维能力的主渠道，教师的引导作用举足轻重，这就要求我们要做一个循循善诱的教师，引导学生向着未知领域探幽发微，逐步走出困境。

启发式诱导

【案例1】已知函数f(x)=x2+2x+a，若对于任意的x∈[1，+∞），f(x)>0恒成立，求实数a的取值范围。

教师诱导：当我看见班级大部分学生这么解时，心里有点惊讶：这帮小孩怎么题目都没审清楚就乱做！我压住心中的怒火，猜想可能部分学生看到了x∈[1，+∞）的条件，只是不知道该怎么用。于是我就试着提醒学生：“请同学们仔细审题，此题的定义域是一切实数吗？”部分审题不清的学生听到这句话后马上有了反应，开始重新解题。可是还有部分学生听到这句话后反而茫然了，这部分学生就是真正不会做的人。这时，我继续提醒：“同学们可以试着画图来研究一下，或者不画图的话，你可不可以想想其他办法来求参数的取值范围，我们在求参数取值范围时最常用的方法是什么？”听到这句话后，很多学生的眼睛发亮了，开始刷刷地写起来。

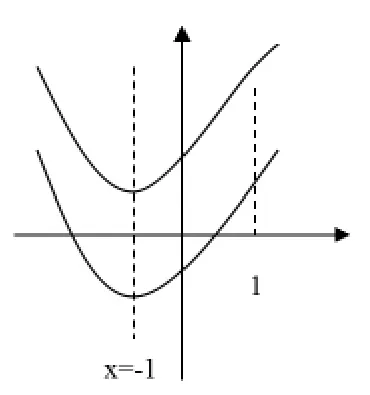
学生再解：

解法一：数形结合。

因为函数f(x)的对称轴为x=-1，

所以只要f(1)>0即可；

即f(1)=3+a>0，

所以a>-3。

解法二：参数分离。

因为f(x)=x2+2x+a>0对于任意的x恒成立，

所以a>-x2-2x对于任意的x∈[1，+∞）恒成立；

即a>(-x2-2x)max。

令g(x)=-x2-2x=-(x+1)2+1，

当x∈[1，+∞）时g(x)单调递减，

所以g(x)max=g(1)=-3，

所以a>-3。

教师反思：当学生解题发生错误时，不要急着告诉他们正确答案，要分析学生出现错误的原因，适当地点拨、启发他们的思维，让他们试着去探索正确的解答。教师的一句启发式诱导语句，有时就像一颗小小的石子，石子虽小，但却能激起学生思维的浪花。

对比式诱导

【案例2】若存在x∈[0，1]，使得2x(x-a)<1，则实数a的取值范围为__。

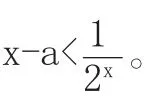
教师诱导：遇到这种情况，我知道学生把存在性问题和任意性恒成立问题混淆了。既然学生混淆了，那我就干脆把原题变一下，让学生先来求这题：“对任意x∈[0，1]，使得2x(x-a)<1恒成立，求实数a的取值范围。”学生一看我在黑板上写下这题，就开始对比这两题的区别，然后试着去做我给的变式练习：

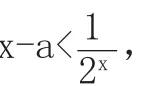
家长群的本质是一种教学和家校沟通工具的延伸，但因为群是半开放的空间，而且具有天然的社交属性，所以常常会变味儿，很多家长群事实上已成为信息过载的“负担群”。怎样在这样一个虚拟的“小社会”里构建合理的秩序呢？这又是另外一个复杂的话题。而我希望，不管是家长还是老师都能在群里多一些理解和包容——至少不要一言不合就把人家给踢了出去。

解好后学生开始疑惑，我就问他们：“解答过程一模一样，难道两道题是同一题目？”学生开始反思。我让学生比较这两类题的区别，仔细体会题目的用词。陆续有学生开始说：“前面一题用的是‘存在’两字，后面一题用的是‘任意’两字。”我马上表扬了这些学生的观察能力，然后继续问：“那你们知道‘存在’和‘任意’的区别吗？”有一些基础较好的学生开始回答：“存在的话只要存在一个满足题意就可以了，任意的话必须是给定范围上的全部都满足题意才可以。”听到这个回答我很开心，正中“要害”，我肯定了他们的回答作做进一步的解释：“对于原题，在给定范围上只要存在g(x)的值比a小就可以了，哪怕只有一个值比a小都能满足题意。那同学们再想想看，a需要比g(x)的最大值还要大吗？”学生思考了一下回到道：“不需要，只要比g(x)的最小值大就可以了。”“很好！那对于后一个变式题，在给定范围上要任意的x都使得g(x)的值比a小，所以a才必须比g(x)的最大值都大。”学生渐渐明白了两题的区别，理解了存在性问题和任意性恒成立问题的本质。

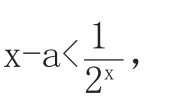
所以g(x)min=g(0)=-1，

所以a>-1。

教师反思：当学生遇到概念或解题方法混乱时，我们可以把学生感到混乱的题放在一起讲，从而从本质上去理解题目，搞清概念，理清思路，弄清方法。

转换式诱导

学生初解：大部分学生不会求解，找不到求解的方法；小部分学生把b换成了1-a或把a换成了1-b，然后通分再利用导数求最值，把问题变得很复杂，最终也没几个人做出来。

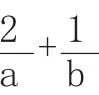
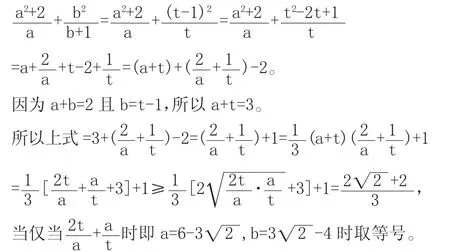
教师反思：当学生遇到一些比较新颖的题不太会做时，我们可以帮助他们去寻找这些“新生儿”的“母亲”，看看能不能用比较相似的基础知识去解决问题，也就是通过转换式诱导——要解决A，我们先从B开始，从而利用B的方法来解决A，达到“曲径通幽”的效果。

帮助学生走出困境的方法是多种多样的，但是最根本的就是要调动学生学习数学的积极性。课堂是思维训练的主阵地，教师在教学中应以思维为核心，以训练为主线，循循善诱，促使学生走出困境。