“教”让道于“思”，让数学思维的火花在课堂中绽放——一道试题的讲评教学实录及反思

□江苏省苏州工业园区青剑湖学校 王小林

“教”让道于“思”，让数学思维的火花在课堂中绽放
——一道试题的讲评教学实录及反思

□江苏省苏州工业园区青剑湖学校 王小林

一、问题的提出

试卷讲评课作为一种重要的课型，在弥补学生的知识漏洞、完善学生的知识结构和方法体系、提高学生的思维能力方面起着至关重要的作用。在试卷讲评课中，作为教师要恰当地把握“教”的度，从而实现学生很好地“思”，“思”出真谛，使课堂的有效性、甚至是高效性得以更好地体现。

二、试题与讲评建议

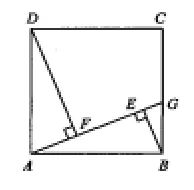
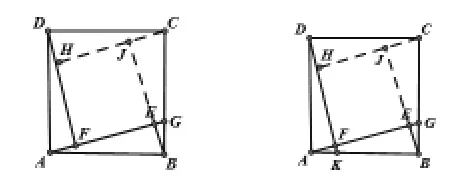
题目：（苏州市2013～2014初二数学基础调研第28题）如图，在边长为1的正方形ABCD中，点G是BC边上的任意一点(不同于端点B、C)，连接AG，过B、D两点作BE⊥AG、DF⊥AG，垂足分别为E、F．

(1)求证：△ABE≌△DAF；

三、调研测试的结果

统计本校初二3个班99名学生，此题的平均分为一班3.5，二班3.3，三班3.1。第一问证明三角形全等基本上人人会做，也就意味着第二问平均分约为0.5、0.3、0.1。换句话说，第二问只有1～2个学生能正确解答此题，说明这个数学问题解决得很不理想。

四、学生的困惑

五、讲评过程实录

师：通过运用AAS不难证明△ABE≌△DAF，从而有对应边相等、对应角相等。第一问作为第二问的铺垫，在此基础上如何求的值？

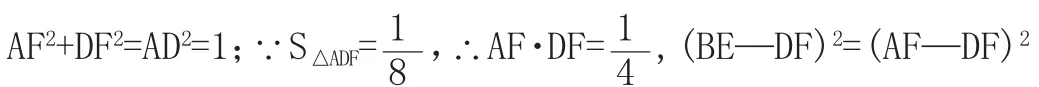
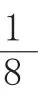
师：冷静和细心是考试获胜的关键因素，只有静下心来才能成功找到条件背后的关系，才能找到正确的解决问题的方法。

师：有没有其他解法？

（学生沉默了些时间）

师：同学们想了这么长时间，能告诉我在想什么吗？

生3：由△ABE≌△DAF得到：BE=AF，DF=AE；∴

师：那么如何求EF？

生3：通过构造“勾股定理弦图”，求EF的值相当于求小

师：能不能在此基础上自编一道题？

生4：简单！延长DF交AB与K，能否证明AK=BG？

生5：可以构造全等三角形从而对应边相等，可以发现，与课本习题刚好形成“逆命题”！

师：精彩！你们真能举一反三！看来，大家已经在不知不觉中进入“题目”了！

至此，这一问题的讲评订正基本结束了，整个过程都是学生在思考、相互合作、展示交流，并体会着问题和方法的不断演变，从而真正掌握解决问题的方法。

六、教学反思

1.试卷讲评要挖掘学生的“试场障碍”。所谓“试场障碍”指的是考试时学生因为紧张、恐惧等心理导致自己不能正确解决问题的一种现象，这个问题如果放在平时练习也许是能够解决的。试卷讲评课要有效引导学生正确处理考试心理问题和考场里突发的问题。

2.试卷讲评要挖掘学生的“解题能力”。比如，在试卷讲评时，笔者不是“教”给学生解题的方法，而是考虑给学生“思”出问题的关键——“图形”，通过构造“勾股定理弦图”使问题轻松解决。通过延长DF交AB于K，实现了与课本习题的“回归”。让出时间，让出空间，从而让出精彩，这才是真正体现学生的主体地位。所以，教师“少”教一些并不意味着自身或学生会有损失，相反，如能多让学生通过自己的“思”，“思”出本质，从而使教学促进学习，而不是控制学习的效果。这样我们的数学课堂定会绽放无穷的魅力！

3.试卷讲评要挖掘学生的“说题思维”。说题是学生运用数学语言口述理清思维脉络，对知识方法进行选择加工的知识构建过程。它不仅有利于数学知识的巩固和应用，而且有利于学生推理论证思维的形成。通过说题训练的教学，让学生大胆开口，很好地“暴露”学生思维的全过程，有利于教师随时掌握知识基础、能力水平，取得较好的效果。如在试卷讲评课中，让学生自行说题、解题，有时比教师在讲台上滔滔不绝的“教”效果更好，因为学生用自己的思维去分析，更贴近他们的思维习惯，更容易被他们理解和接受。教师只需点评，在关键的地方示范板演。说题可设置以下问题链：（1）此题的解法是？你是怎么想出来的？（2）难点在哪里？关键是哪一步？（3）能找到更好的解题途径吗？能否寻求“一题多解”呢？（4）这种方法能推广吗？（5）通过解决这个问题，我学到了什么新知识？从中得到什么启发？这样的过程很好地体现了“数学教学活动是数学活动的教学，是师生之间、学生之间交往互动与共同发展的过程”的教学新理念。

孔子曰：“吾日三省吾身。”作为教师，应“日省”如何适度的“教”，给学生“思”的空间，让他们自主探究，学会对数学知识进行思维加工。要充分发挥学生的主体作用，变学生的学习过程为在教师引导下实现知识“再创造”的过程，使学生在潜移默化中获得知识，学会方法，真正把学生从“题海”中解放出来，切实提高教学活动的有效性！