氮气在缩放喷管中非平衡自发凝结的数值研究

孙皖,牛璐,赖天伟,刘立强,侯予

(1.西安交通大学动力工程多相流国家重点实验室,710049,西安; 2.中国科学院低温工程学重点实验室(理化技术研究所),100190,北京)



氮气在缩放喷管中非平衡自发凝结的数值研究

孙皖1,牛璐1,赖天伟1,刘立强2,侯予1

(1.西安交通大学动力工程多相流国家重点实验室,710049,西安; 2.中国科学院低温工程学重点实验室(理化技术研究所),100190,北京)

针对氮气在收缩型喷管中自发凝结的两相流动,采用经典成核理论来计算气液两相间的质量传递,选用Standard Redlich Kwong气体状态方程,忽略了气液相之间的速度滑移,利用商业软件CFX中的非平衡凝结模型进行了二维数值模拟。通过对成核率的量级、压力和带液量变化趋势及开始凝结的位置等模拟结果的分析,验证了模型和数值计算的有效性。进一步的数值模拟结果表明:相比于无凝结的绝热膨胀过程,相变释放潜热及气液之间的导热会加热气体,使得气流压力升高、马赫数降低。平衡凝结模型及非平衡凝结模型的对比显示,非平衡数值模型能够更好地揭示低温下氮气自发凝结的两相膨胀过程。

自发凝结;非平衡;喷管;成核

自发凝结两相流动的研究是低温两相膨胀的基础问题,也是低温两相透平膨胀机设计的关键和难点。在氮气三相点(63.15 K)以上的低温区,空气或者氮气膨胀可能会发生凝结相变,其热力学不可逆损失会严重影响其流动特性,并在很大程度上影响理论分析和实验结果的准确性。自从文献[1-2]提出经典成核理论以来,关于气液成核的实验与数值研究主要集中于水物质,对于空气及氮气低温下的成核问题,由于关键物性的不确定性以及分子间势能理论的缺乏,使得其实验与模拟都非常困难。以氮气为例,文献[3]在超音速风洞中研究了氮气成核,文献[4]通过测量静压及光散射在超高音速喷管中检测到氮气成核的发生,之后许多学者相继利用超音速喷管[5-6]、激波管[7-8]或者成核脉冲室[9]对氮气进行了Wilson点的测量以及成核率的计算。但是,上述研究都针对氮气三相点以下的温区,氮气凝结有可能会产生固态粒子。对于三相点以上的温区,氮气凝结的研究工作比较少,文献[10]利用NASA Langley 0.3 m低温风洞进行了氮气凝结实验与理论分析,但流动发生在CAST-10机翼外部。文献[11]对氮气在喷管内部流动中的凝结采用两种成核理论进行了数值模拟,但模型只与机翼外部流动的实验进行了对比。

本文采用商业软件CFX中的非平衡凝结模型,模拟了在低温下缩放喷管中氮气自发凝结的两相膨胀过程,首先分析了模拟结果,并与文献[11]的数值计算结果进行了对比验证,然后分析了自发凝结对于流动特性的影响,最后完成了与平衡凝结模型的对比与分析。

1 数值模型

1.1 控制方程

在CFX的非平衡凝结模型中,气液两相都有各自的守恒控制方程,通过方程的源项来实现气相与液相之间的质量与热量传递。由于形成的液滴半径很小(通常小于1 μm),且出口湿度很小不会产生大的二次液滴,因此液滴与气相之间为速度无滑移。

基于上述假设,欧拉方程的通用形式为

(1)

式中:x、y和t分别为空间坐标和时间坐标;U、E、F和S分别为

式中:u和v分别对应气液相x和y方向的速度;ρ为气相或者液相的速度;htot为总比焓值;p为静压;T为气相或者液相的温度;λ为导热系数;Sm为质量方程源项;Su和Sv为动量方程源项;SE为能量方程源项。

另外,为了使控制方程能够进行封闭求解,对于液相还有一个对应的液滴数量守恒控制方程

(2)

式中:下标“l“和“g”分别代表液相和气相;Nl为单位体积内的液滴数量,单位为m-3;γg为气相体积分数;J为成核率,即单位体积、单位时间内所产生液滴的个数,单位为m-3·s-1。

1.2 成核模型及液滴生长模型

自发凝结过程中的气液两相间的质量传递由两部分组成,一是由于自发凝结成核而产生的质量传递,二是在已产生的凝结核心上液滴生长所带来的质量传递。在CFX的非平衡凝结模型中,对于成核率计算采用经典成核模型的形式

(3)

式中:A是由特定成核模型决定的常数;k为波尔里兹曼常数;ΔG*是临界成核半径液滴的吉布斯自由能变;Tg为过冷气体的温度。

对于液滴生长率则采用如下计算式

(4)

式中:Rl为液滴的半径;Kn为克努森数;hg和hl分别为气体和液体的比焓值。

因此,由于凝结相变所引起的气液质量、动量及能量的传递,表现为源项的计算式如下。

(1)质量方程源项

(5)

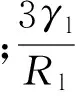
(6)

(2)动量方程源项。由于气液两相速度是相同的,则动量方程源项Su和Sv均为0。

(3)能量方程源项。能量方程源项SE由两部分组成,一部分是由于质量传递引起的热量传递,另一部分是气液之间导热产生的热量传递,其计算公式为

(7)

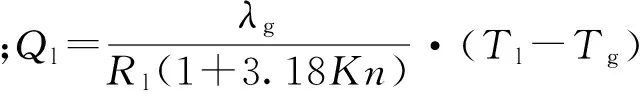
称取样品5 g剪碎，加入45 ml无菌蒸馏水，在5 ℃条件下浸泡0. 5 h,待其充分浸泡后，用电子酸度计测定。

液滴的温度计算如下

(8)

1.3 状态方程

对于非平衡凝结过程,气体达到饱和线后会继续进入过冷状态,因此气体状态方程必须能够外推到过冷区域,在CFX中StandardRedlichKwong方程[13]满足这一要求。其表达式为

(9)

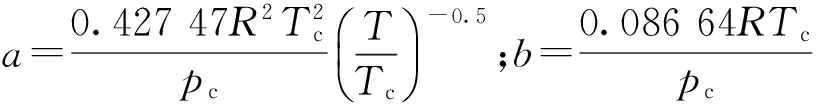
饱和线采用文献[14]提出的形式

(10)

式中:ω为偏心因子。

1.4 几何模型及数值方法

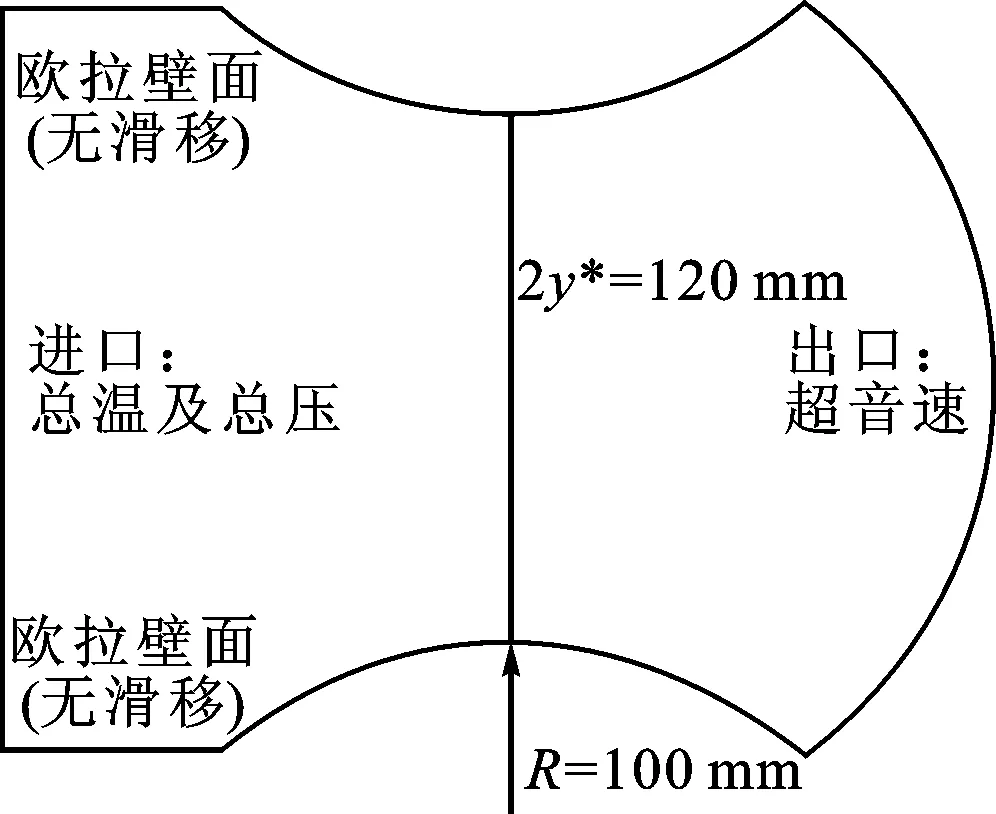
图1 喷管的几何尺寸及边界条件

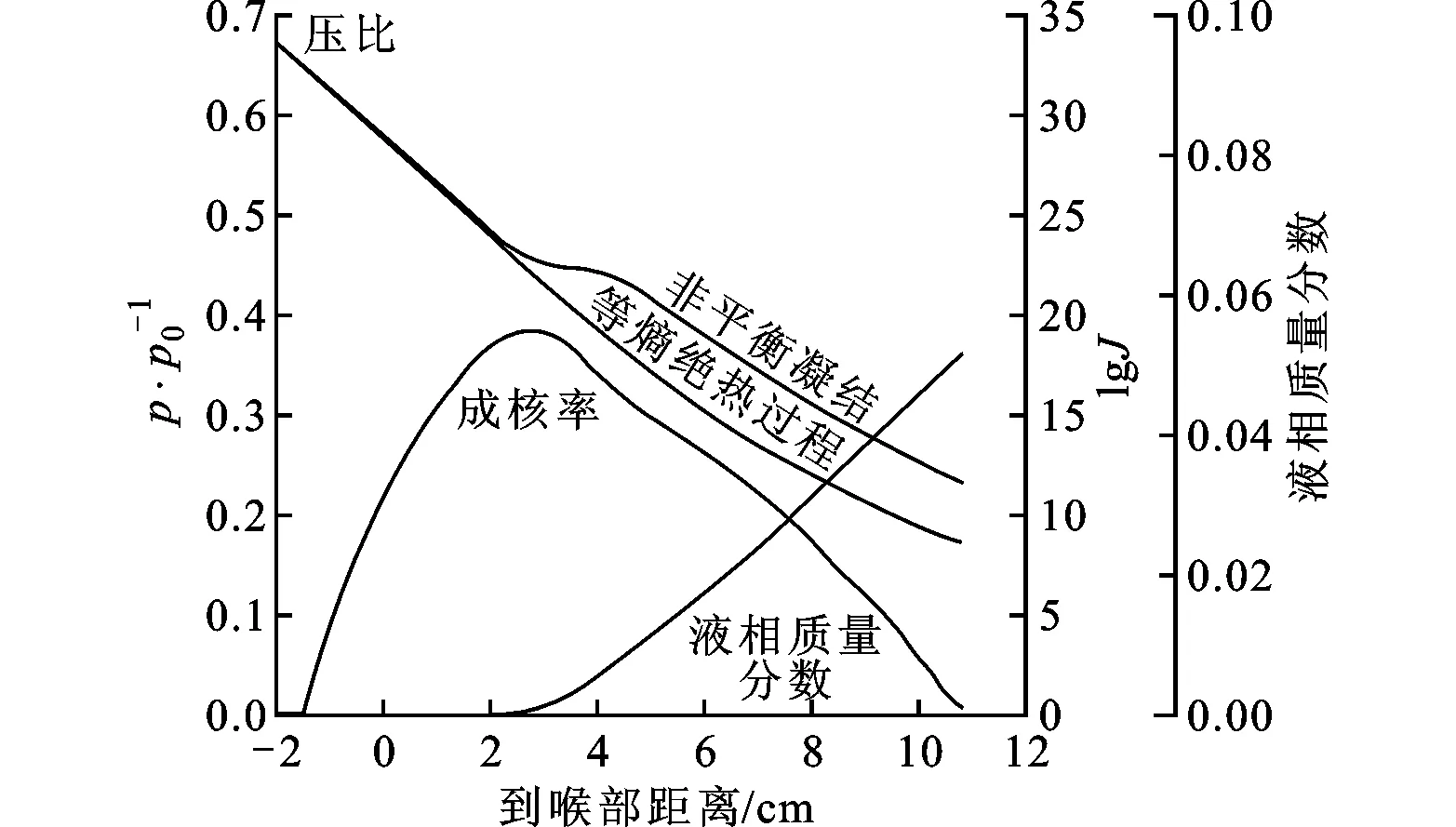
(a)ASHRAEModGya模型[11]

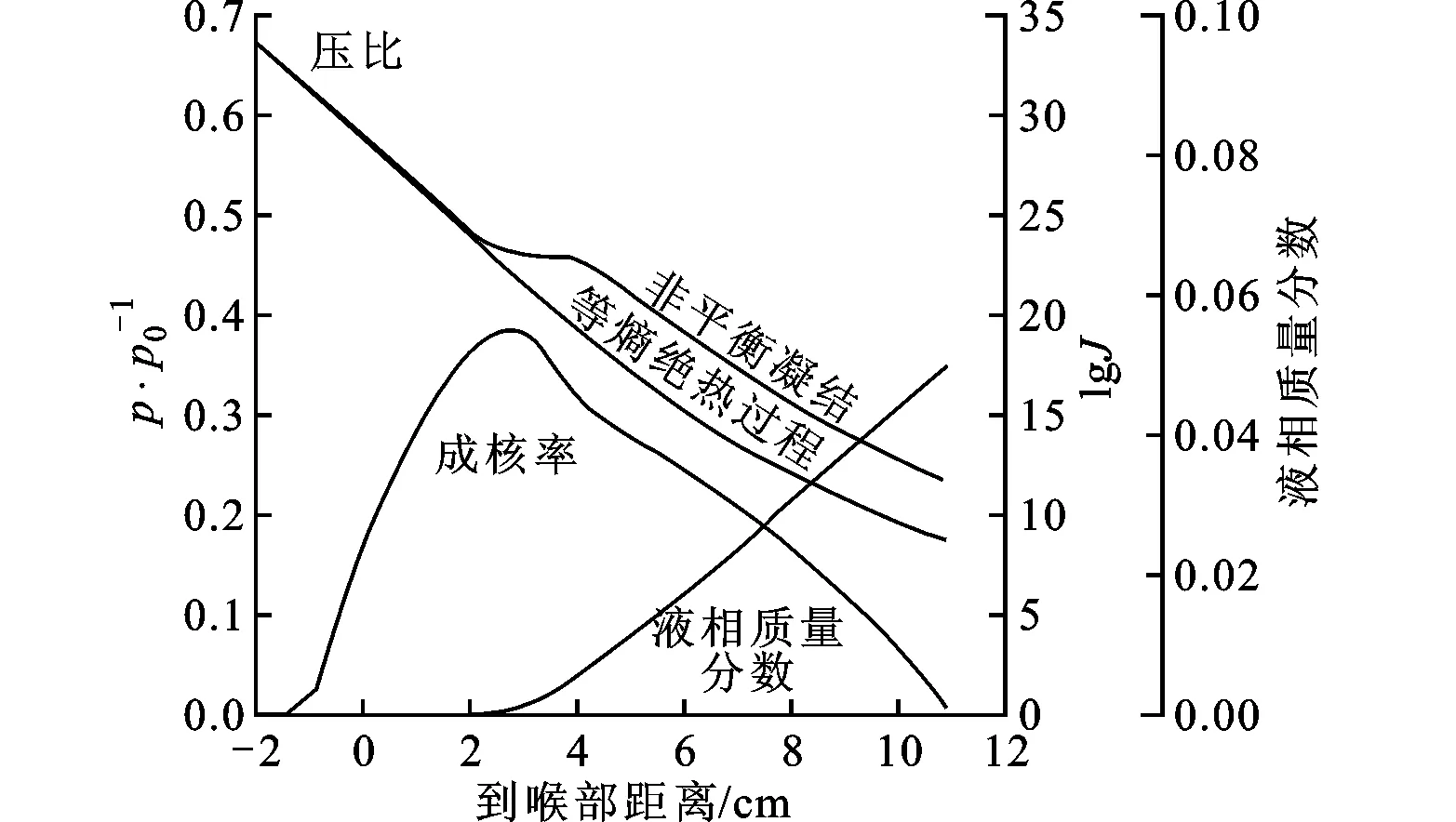
(b)EotvosHKMac模型[11]

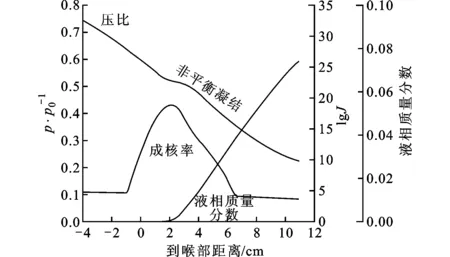
(c)本文数值模型图2 3种模型模拟结果的对比

2 模拟结果

在非平衡凝结的研究中,成核率是一个重要参数,不同的成核理论计算的成核率甚至会有10以上数量级的差别。图2为压力、成核率及液相质量分数(带液量)沿流道中心线的变化趋势,图2a和图2b为文献[11]中两种模型模拟结果,成核率大约为1019m-3·s-1,图2c为本文的模拟结果,成核率大约为1018m-3·s-1,成核率的量级基本一致,同时成核率最大的位置(即开始凝结的位置)在喉部下游0.02 m左右处,与文献中也基本吻合,另外压力及带液量的变化趋势也是一致的。然而,压力、成核区间的宽度以及带液量的最大值与文献对比都有一定的差别,这可能是因为采用了不同的成核模型及液滴生长模型导致的。

由图2a和图2b可以看出,与没有凝结相变的绝热膨胀过程相比,在开始凝结的区域,相变潜热及气液间的导热会加热气流,使压力降低变缓,同时减速气流,使马赫数增加变缓,压力和马赫数分布分别如图3、图4所示。这些都符合实际情况,由此可见自发凝结过程对流动性能的重要影响。

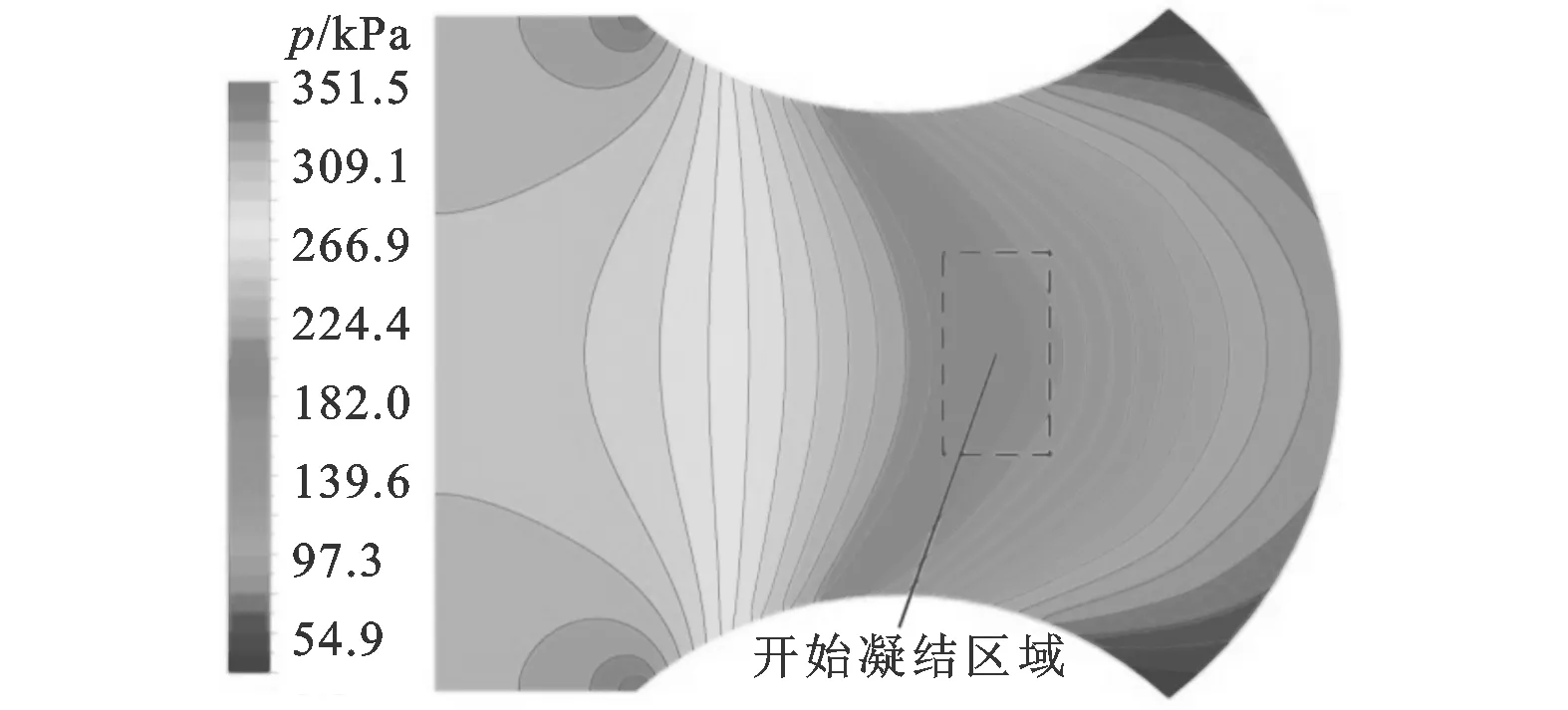
图3 非平衡凝结模拟压力云图

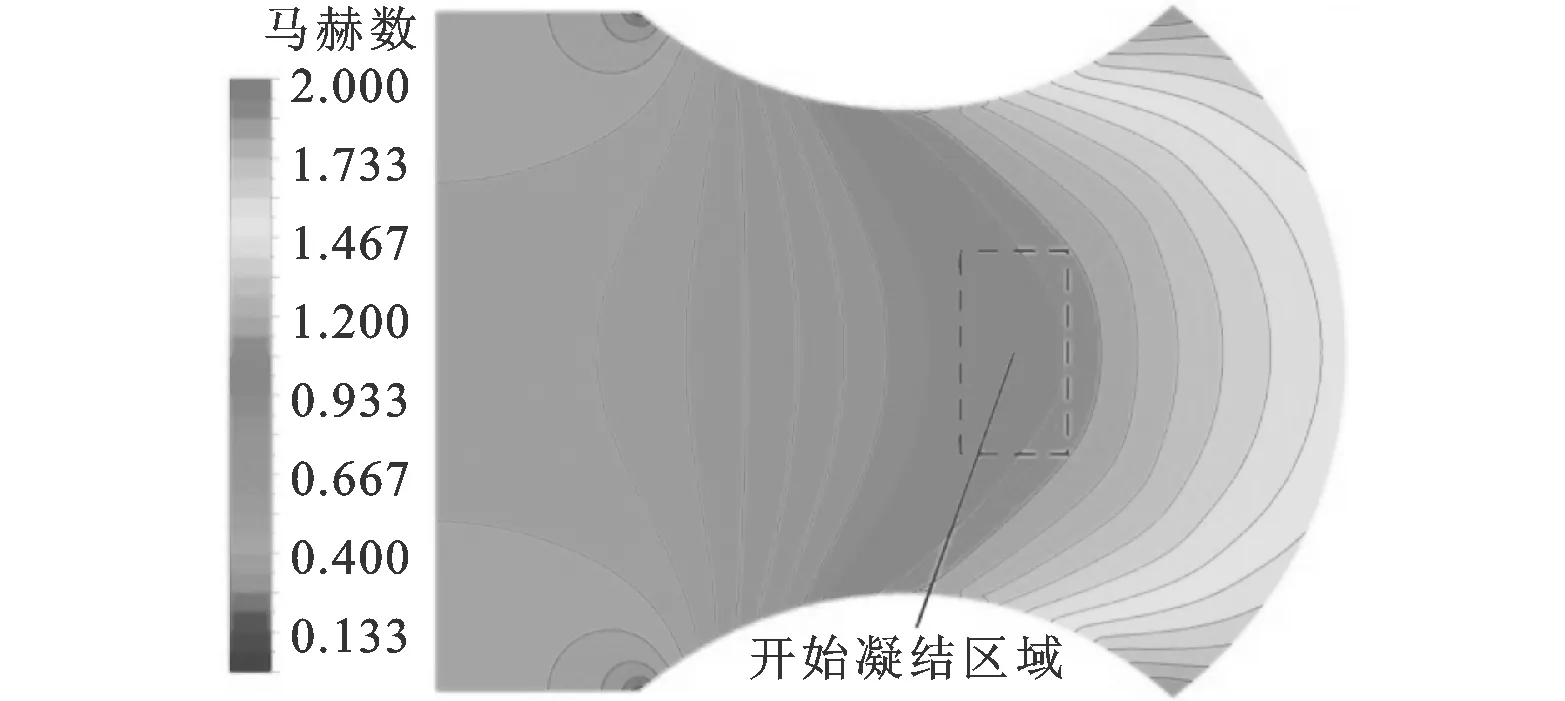
图4 非平衡凝结模拟马赫数云图

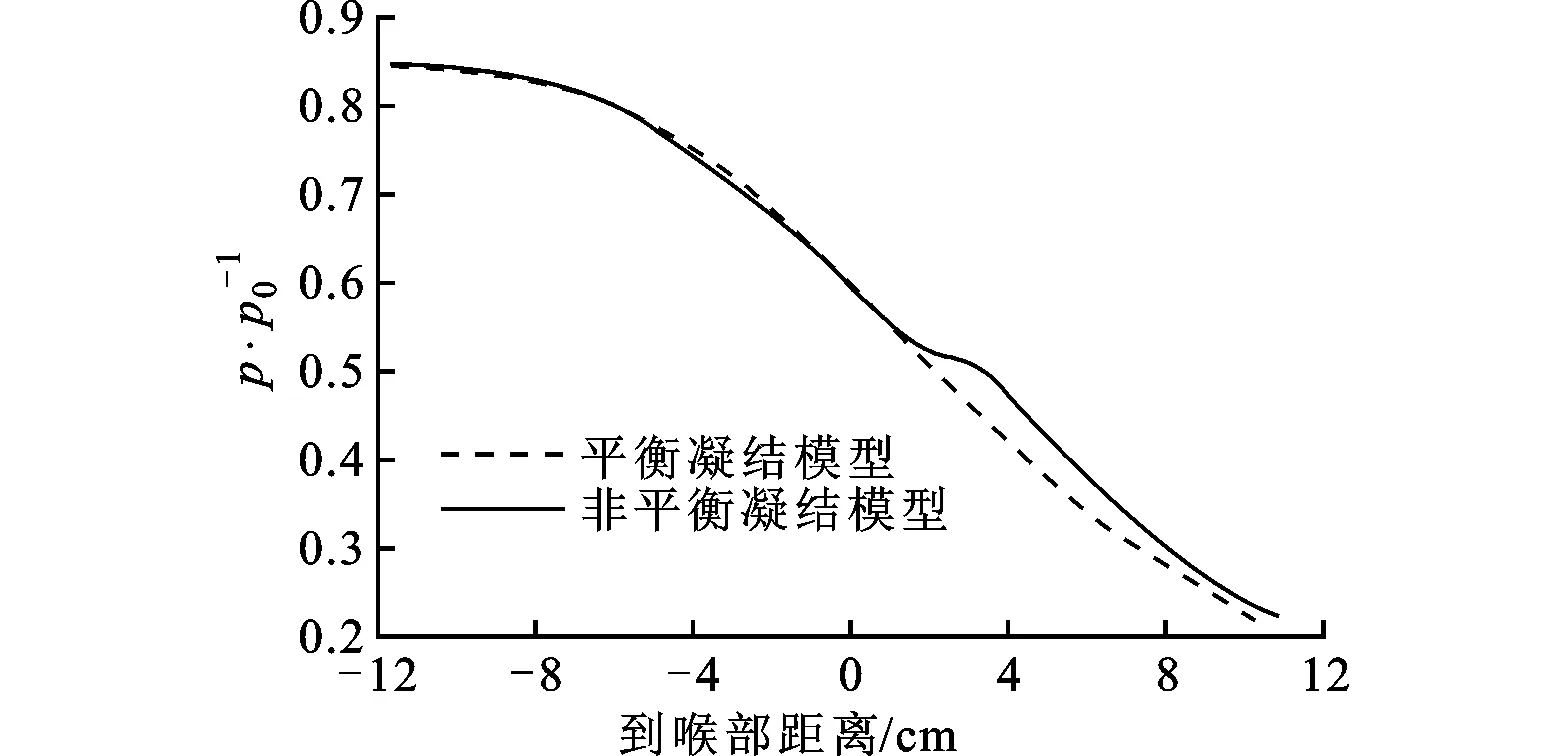
图5 两种模型压力沿流动中心线变化趋势的对比

图5所示为平衡凝结模型[15]与非平衡凝结模型的压力沿流动中心线的变化趋势对比,从中可以看出,平衡凝结模型不可逆损失只考虑了相变潜热,因此压力的变化是均匀的,对于流动特性的影响并不明显。再由图6两种模型的带液量云图对比可以看出,非平衡凝结模型由于是在气体达到一定过冷时才产生液滴,因此开始凝结的位置滞后于平衡凝结模型,而且最大带液量也有所减少。

(a)平衡凝结模型

(b)非平衡凝结模型图6 平衡凝结模型和非平衡凝结模型的带液量云图对比

3 结 论

本文利用CFX中的非平衡凝结模型对氮气在一缩放喷管中自发凝结的两相膨胀过程进行了数值模拟,进出口条件均在氮气的三相点(63.15 K)以上,得到结论如下。

(1)成核率量级、压力和带液量变化趋势及开始凝结的位置与文献数据基本一致,验证了本文模型与假设的有效性。

(2)在开始凝结的区域,相变潜热及气液间的导热会加热气流,使得气体膨胀过程变缓,与无凝结的绝热膨胀过程相比,表现为压力下降及马赫数上升趋势均变缓,因此自发凝结过程对流动性能有着重要影响。

(3)与平衡凝结模型进行对比,非平衡凝结模型更加准确地表现了流动特性,开始凝结的位置相对滞后,带液量也有所减少。

[1]BECKE R, DORING W.Kínetische behandlung der keimbildung in übersättigten dämpfen [J].Annalen der Physik, 1935, 46(8):719-752.

[2]VOLMER M.Kinetik der phasenbildung [M].Dresden, Germany:Steinkopff, 1939:1-220.

[3]FARO I, SMALL T R, HILL F K.The supersaturation of nitrogen in a hypersonic wind tunnel [J].Journal of Applied Physics, 1952, 24(1):40-43.

[4]WILLMARTH W W, NAGAMATSU T.The condensation of nitrogen in a hypersonic nozzle [J].Journal of Applied Physics, 1952, 23(10):1089-1095.

[5]KOPPENWALLNER G, DANKERT C.Homogeneous condensation in nitrogen, argon, and water vapor free jets [J].Journal of Physical Chemistry, 1987, 91(10):2428-2486.

[6]BHABHE A, WYSLOUZIL B.Nitrogen nucleation in a cryogenic supersonic nozzle [J].Journal of Physical Chemistry, 2011, 135(24):244311.

[7]ZAHORANSKY R A.Nitrogen nucleation in an unsteady supersonic flow field [J].Zeitschrift fur Flugwissenschaften und Weltraumforschung, 1986, 10(1):34-37.

[8]STEINWANDEL J.Homogeneous condensation of nitrogen in the expansion wave of a cryogenic shock tube [J].Ber Bunsenges Phys Chem, 1985, 89(5):481-484.

[9]ILAND K, WEDEKIND J, WOLK J, et al.Homogeneous nucleation of nitrogen [J].Journal of Physical Chemistry, 2009, 130(11):114508.

[10]DOTSON E H.Homogeneous nucleation and droplet growth in nitrogen [R].Hampton, USA:Joint Inst for Advancement of Flight Sciences, 1983.

[11]GOODHEART K A.3-D transonic flow dynamics with nonequilibrium condensation [D].Munich, Germony:Technische Universität München, 2004.

[12]ANSYS Inc..ANSYS CFX:solver theory guide [M].New York, USA:ANSYS Inc., 2010:209-212.

[13]REDLICH O, KWONG J N S.On the thermodynamics of solutions:V An equation of state, fugacities of gaseous solutions [J].Chemical Reviews, 1949, 44(1):233-244.

[14]POLING B E, PRAUSNITZ J M, O’CONNELL J P.The properties of gases and liquids [M].Fifth ed.New York, USA:McGraw-Hill, 2001:7.1-7.3.

[15]孙皖, 马斌, 牛璐, 等.低温透平膨胀机内平衡凝结两相流动的数值模拟 [J].西安交通大学学报, 2013, 47(7):36-39.SUN Wan, MA Bin, NIU Lu, et al.Numerical simulation of equilibrium condensation two-phase flow in cryogenic turboexpander [J].Journal of Xi’an Jiaotong University, 2013, 47(7):36-39.

(编辑 杜秀杰)

Numerical Research on Nitrogen Spontaneous Condensation in Converging-Diverging Nozzle

SUN Wan1,NIU Lu1,LAI Tianwei1,LIU Liqiang2,HOU Yu1

(1.State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190, China)

Assuming a homogeneous flow without velocity slip between gas and liquid phases, 2-D numerical simulation for predicting nitrogen expansion flow with spontaneous condensation in a converging-diverging nozzle is accomplished via the non-equilibrium model of CFX.The mass transfer between two phases is calculated with the classical nucleation model and the standard Redlich Kwong state equation.The magnitude of nucleation rate, pressure and condensate mass fraction distributions, and condensation onset are comparatively analyzed to verify the validation of the model.Compared with the adiabatic expansion without condensation, the flow is heated by the latent heat and thermal conductivity between gas and liquid phases to heighten pressure and lower Mach number.A comparison between equilibrium condensation model and non-equilibrium condensation model shows better prediction of the latter for nitrogen expansion with spontaneous condensation.

spontaneous condensation; non-equilibrium; nozzle; nucleation

2014-06-17。 作者简介:孙皖(1988—),男,博士生;侯予(通信作者),男,教授,博士生导师。 基金项目:教育部高等学校博士学科点专项科研基金资助项目(20130201110038);中国博士后科学基金资助项目(2014M552438);陕西省国际科技合作重点资助项目(2014KW09-01);中国科学院低温工程学重点实验室开放课题资助项目(CRYO201318)。

时间:2014-10-31

http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.015.html

10.7652/xjtuxb201504021

TB653

A

0253-987X(2015)04-0130-04