水中金属丝电爆炸冲击波一维数值模拟

李兴文,晁攸闯,吴坚,贾申利,邱爱慈

(西安交通大学电力设备电气绝缘国家重点实验室,710049,西安)



水中金属丝电爆炸冲击波一维数值模拟

李兴文,晁攸闯,吴坚,贾申利,邱爱慈

(西安交通大学电力设备电气绝缘国家重点实验室,710049,西安)

为了明确水中金属丝电爆炸冲击波的形成机理,基于经典活塞模型,采用相似参数法,引入双人工黏性系数,建立了水中金属丝电爆炸冲击波的一维计算模型。以等离子体放电通道边界膨胀轨迹作为模型唯一的输入参数,得到水中冲击波传播的时间与空间的分布规律,通过与其他文献实验结果的对比,验证了该计算方法的有效性。模拟结果表明,双人工黏性系数法使计算得到的冲击波更符合实际情况。爆炸初始时刻,等离子体放电通道边界膨胀压缩周围水介质产生的冲击波高达GPa级,冲击波压强峰值与径向传播距离的-0.70次幂成正比关系。文中采用的计算方法既不涉及脉冲放电过程以及复杂的放电等离子体物理变化过程,也不涉及放电通道与水的物理化学作用过程,只需根据诊断实验得到放电通道边界膨胀轨迹,即可模拟水中金属丝电爆炸冲击波的产生与传播过程,对工程实践具有重要的指导意义。

水中放电;金属丝电爆炸;冲击波;人工黏性系数;等离子体

水中金属丝电爆炸现象伴随着丰富的物理过程,并具有很宽的温度与密度跨度。在高功率电脉冲的作用下,金属丝历经固、液、气三相,最终形成高温、高压的等离子体,并与水介质相互作用,释放出强冲击波。这些特点使得水中金属丝电爆炸现象具有丰富的理论研究价值与实际应用价值,并成为脉冲功率技术领域一个前沿的研究热点。目前,该项技术被广泛应用于冲击波热核聚变、纳米材料制备、脉冲陡化以及污水处理等[1-2],还可用于产生温密物质[3]。水介质击穿场强高(～3×105V/cm)、难以压缩(绝热系数γ=7.15),与真空电爆炸相比,水中金属丝电爆炸过程无冕层击穿现象[4],这导致金属丝能量沉积率极高,产生的冲击波通常具有100 MPa以上的幅值与100 μs量级甚至更短的脉宽。

目前,对水中金属丝电爆炸的物理过程描述存在着2种理论模型:冲击波传播模型[5]和磁流体动力学模型[6-7]。冲击波传播模型利用实验中获取的金属丝早期等离子体通道速度作为边界条件,计算等离子体通道活塞推动下冲击波的传播过程。这一模型可以获取介于等离子体通道与冲击波前沿水介质的密度与压强,进而计算出冲击波的压强及电能到机械能的转化效率。磁流体动力学模型致力于获取金属材料或水在极端(高温、高压)条件下的物性参数,主要用于结合实验数据推算电导率与验证状态方程,包括文献[6]建立的一维单温近似磁流体动力学模型与文献[7]建立的一维辐射磁流体动力学模型。冲击波传播模型仅对能量转化效率进行了推算,未能得到真实冲击波的传播机制,并且计算结果也不是很理想。磁流体动力学模型更多关注于金属丝本身的物理过程,其中对电离水层的描述也主要集中于分析能量沉积过程,对等离子体放电通道和水介质相互作用过程产生冲击波的机理描述不充分。

然而,水中电爆炸冲击波的产生与传播机理对工程实践具有巨大的应用潜力,因此建立实用的冲击波计算模型对于工程实践具有重要的理论指导意义。基于此,本文对已有冲击波传播模型[5,8]进行改进,建立了用于计算水中金属丝电爆炸冲击波的产生与传播特性的一维流体力学模型。该方法从理想可压缩流体基本假设出发,首先推导了描述理想冲击波传播特性的无量纲化控制方程组,然后引入双人工黏性系数,通过选取不同的黏性系数,对计算结果进行了对比与分析。这既不同于Veksler等人通过直接求解理想流体控制方程来获得冲击波的计算方法[8],也不同于Grinenko等人所提出的只将人工黏性系数引入欧拉方程的单人工黏性系数计算方法[5]。双人工黏性系数的引入,不仅使所计算得到的冲击波速度、压强时间与空间分布更为符合实际冲击波的物理参数分布,而且也考虑了实际波阵面存在一定厚度,使计算得到的冲击波波阵面前后速度与压强呈连续性变化,而不是理想冲击波波阵面物理参数的阶跃式变化。

本文将文献[8]采用条纹相机拍摄到的等离子体放电通道发展速度作为该模型的输入参数,进行了数值计算,通过与其文献实验结果的对比,验证了本文计算模型的有效性。

1 数值计算模型

在水中金属丝电爆炸过程中,金属丝将经历固、液、气和等离子体的状态演变。金属丝在液态过热过程中处于高温、高压状态,甚至有可能接近甚至超过其临界点条件,所以当气化开始后,金属丝将剧烈膨胀形成相爆。当轴向场强足够大时,金属蒸气被击穿,形成等离子体放电通道,类似于活塞推动周围水介质运动,从而形成冲击波。

1.1 控制方程

由于脉冲放电时间短(μs级),该过程中可以忽略流体的黏性,而流体的惯性必须考虑。同时,考虑到金属丝电爆炸过程形成的等离子体放电通道为圆柱形通道,可认为形成的冲击波物理参数为轴对称分布,在一维柱坐标系下只存在径向分量,则通道周围流体运动过程的连续性方程和Euler运动方程可表示为[9]

(1)

(2)

式中:ρ、u、p分别为流体的密度、速度、压强。Euler运动方程考虑了流体的可压缩性,适于理想可压缩流体的计算。

为了求解式(1)、式(2),需要给出压强和内能的热力学方程。在压强小于10 GPa的条件下,水的状态方程可以采用Tait状态方程

(3)

式中:p为放电通道周围液体压力;p0为环境压力,取1.01×105Pa;ρ0为水的平衡态密度;A和γ为常数,对于常态条件下的水[10],可以取A=3×108Pa,γ=7.15。通过式(1)～式(3),可以得到

(4)

(5)

式中:引入了无量纲声速C≡c/c0,c0≡(Aγ/ρ0)1/2为静止水的当地声速;无量纲时间τ≡c0t/D0,D0为电爆炸丝初始直径;无量纲流速U≡u/c0;无量纲坐标R≡r/D0。

1.2 人工黏性系数的引入

冲击波是可压缩流体运动过程中的一种重要现象。从物理上看,冲击波是流体流动过程中宏观状态参量发生剧烈变化的一个极薄的区域(冲击波波阵面),所有流动参量,如压强、速度、密度等在跨越这个面时都不是很连续的,理想冲击波是没有厚度的。在实际情况下,冲击波有一个有限的、并且可以测量的厚度[11],如图1所示。

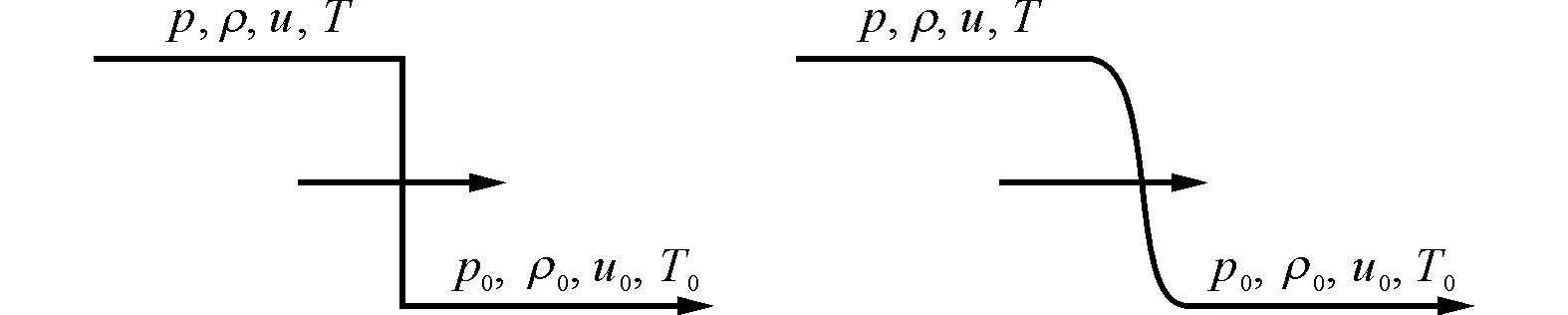
(a)理想冲击波 (b)实际冲击波图1 冲击波波阵面

由于理想冲击波波阵面前后物理参数不连续,如图1a所示,所以直接采用数值方法求解理想流体控制方程,会导致计算结果产生较大误差。文献[12]考虑到实际冲击波波阵面有一定的厚度,将带有人工黏性系数的二阶导数作为耗散项引入到流体力学方程中,建立了人工黏性法。文献[5]采用单人工黏性法建立了水中冲击波的传播模型,只将黏性系数引入运动方程,连续性方程并未引入黏性系数,使计算得到的速度空间分布更符合实际冲击波的速度空间分布,但计算得到的压强空间分布并不是很理想。因此,本文对文献[5]的单人工黏性系数冲击波传播模型进行改进,将人工黏性系数同时引入式(4)、式(5),使计算得到的冲击波波阵面前后压强也呈连续性变化。于是,式(4)、式(5)可以写成

(6)

(7)

式中:μ1、μ2为人工黏性系数。

1.3 边界条件和初始条件

求解式(6)、式(7)需要一组初始条件与两组边界条件。取水的环境压力p0=1.01×105Pa,标准大气压下水的密度与当地声速分别取ρ0=103kg/m3和c0=1 500 m/s。初始时刻周围水为静止状态,即p=p0,ρ=ρ0,u0=0 m/s,相应的无量纲参数分别为C(R,τ=0)=1、U(R,τ=0)=0。其中一组边界条件为等离子放电通道膨胀速度,即Up(R=0,τ)=dRp(τ)/dt;另一组边界条件为无穷远边界条件,即p(R=∞,τ)=p0,ρ(R=∞,τ)=ρ0,U(R=∞,τ)=0 m/s,相应的无量纲参数U(R=∞,τ)=0,C(R=∞,τ)=1。

以文献[8]实验得到的放电通道边界运动轨迹作为模型第一组边界条件,如图2、图3所示。图2给出了等离子体通道边界与冲击波前沿径向传播距离,0时刻对应于放电电流起始时刻。图3给出了等离子体放电通道边界径向传播速度随时间变化的曲线,由基于文献[13]总结的速度经验公式得到。本文采用多物理场Comsol Multiphysics 4.3a有限元商业软件进行模拟计算。

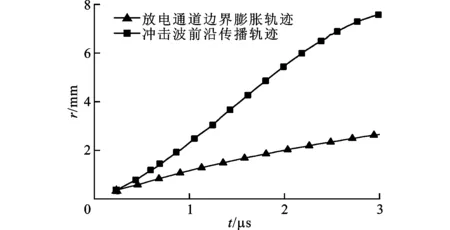
图2 等离子体通道边界与冲击波前沿径向的传播距离

图3 等离子体放电通道边界径向传播速度随时间变化曲线

2 计算结果与分析

2.1 黏性系数对计算结果的影响

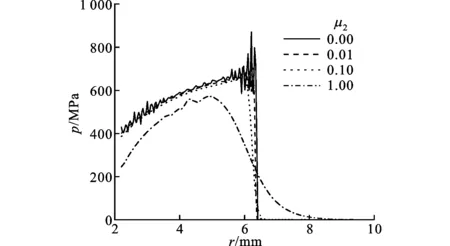
(a)μ1=0.1

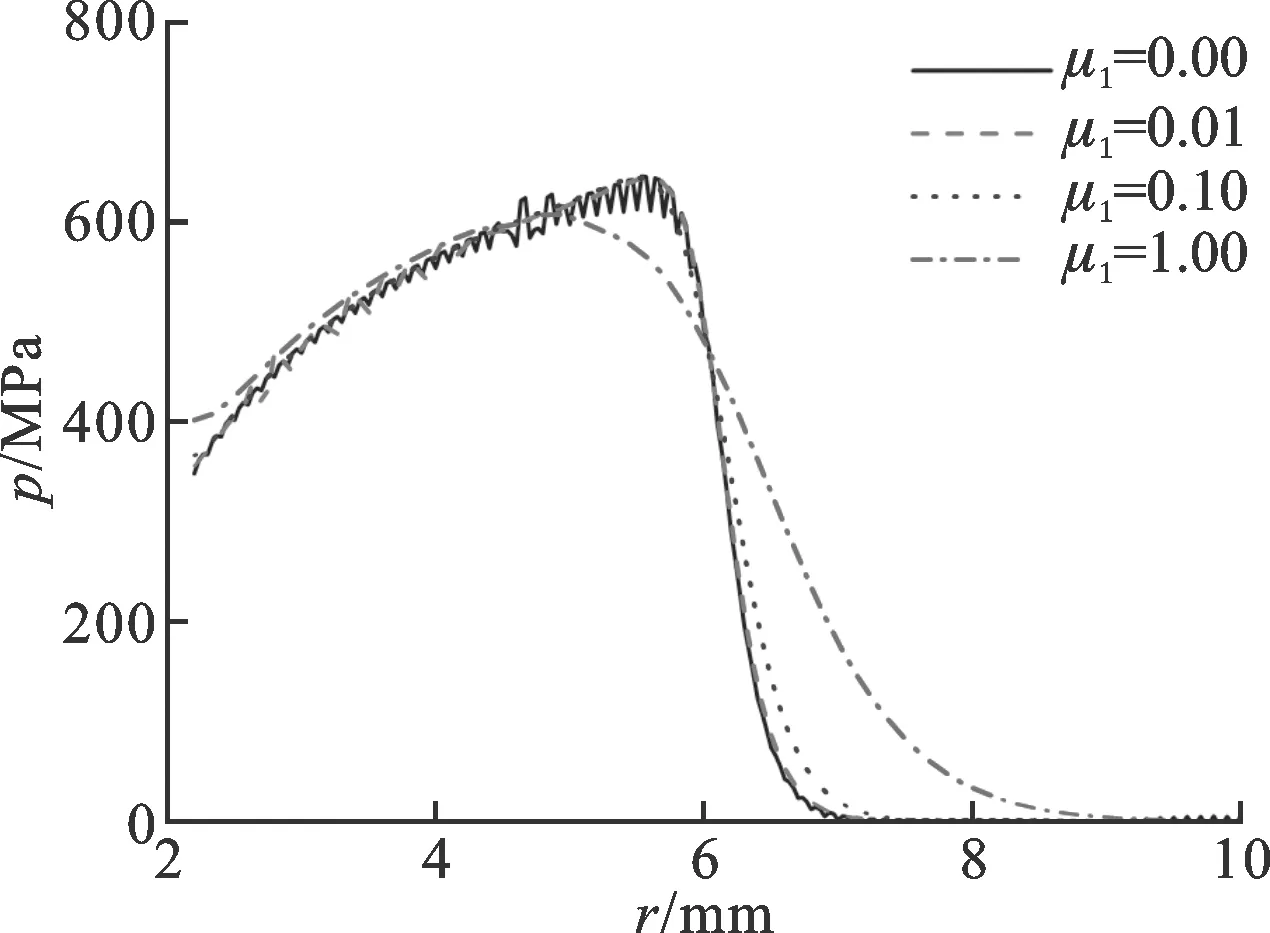
(b)μ2=0.1图4 t=3 μs时不同黏性系数下压强径向分布

图4分别显示了3 μs时,黏性系数μ1、μ2分别取不同值时,采用参数化扫描方法计算得到的冲击波压强径向分布图。从图4中可以发现:当黏性系数过小时,计算得到的冲击波附近水流速度和压强振荡较为剧烈;当黏性系数过大时,计算得到的冲击波前沿变化过慢,不能准确描述波阵面前后物理参数的突变。此外还可以看出,μ2比μ1对计算得到的冲击波压强空间分布的影响更为显著。

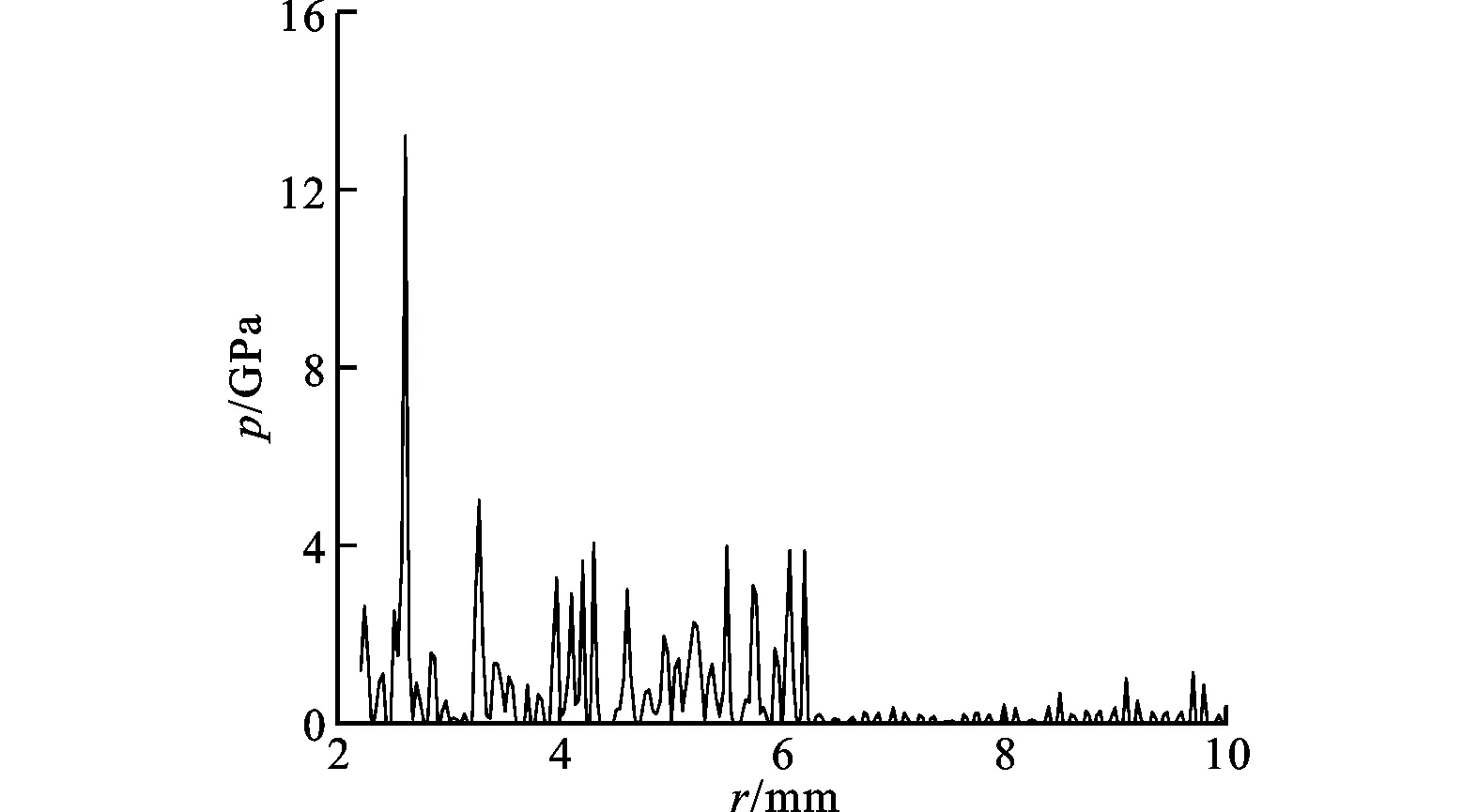
(a)无人工黏性系数法计算结果

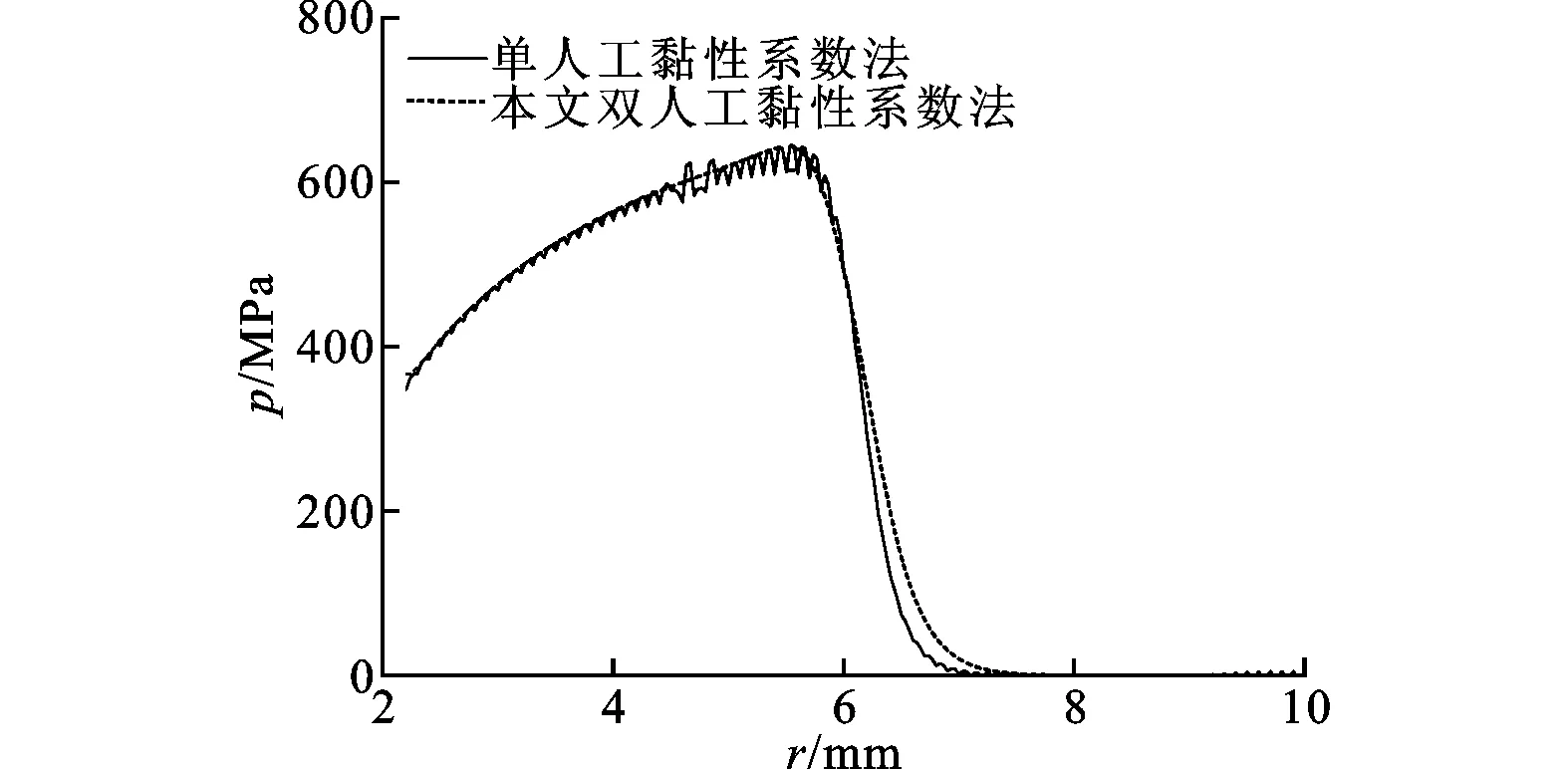
(b)单人工与双人工黏性系数法计算结果图5 不同计算方法下的压强径向分布情况

图5所示为3 μs时无人工黏性系数法、单人工黏性系数法[5]与本文双人工黏性系数法计算结果的对比,可见3种计算方法都能达到收敛,然而未引入人工黏性系数的计算结果与实际冲击波压强空间分布情况相差较远。与单人工黏性系数法相比,本文采用的双人工黏性系数法计算结果更符合实际冲击波压强空间分布(见图1)。

2.2 放电通道与冲击波之间水介质物理参数分布

从图4可以看到,选取黏性系数μ1=μ2=0.1,可使计算得到的压强径向分布曲线较为平滑,能较好地描述冲击波波阵面前后物理参数的空间分布。图6、图7分别给出了当黏性系数都取0.1时,不同时刻放电通道与冲击波之间水介质压强与速度的径向分布。从图6明显看到,等离子体放电通道通过活塞膨胀作用推动周围水介质运动,初始时刻放电通道周围水介质压强高达GPa级。介于等离子体放电通道和冲击波波阵面之间水介质压强随径向距离不断增加,而速度呈相反趋势,随着时间的增加,冲击波不断向前推移。此外,还可以观察到冲击波波阵面存在一个过渡的过程,反映了流体质点从一个平衡态过渡到另一个平衡态的弛豫过程。正是由于双人工黏性系数的引入,使得计算得到的冲击波物理参数更符合实际情况。

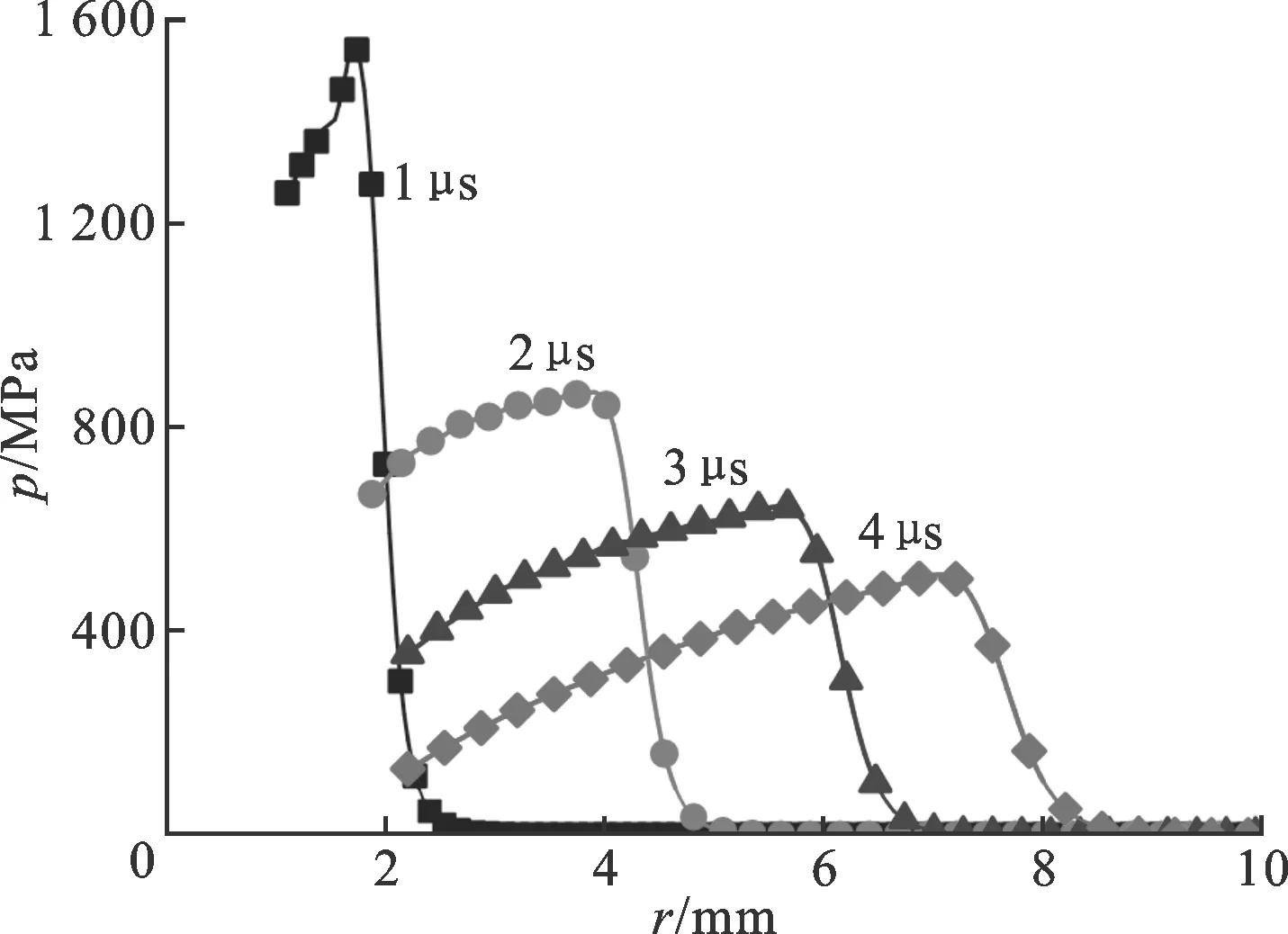
图6 不同时刻的压强径向分布曲线

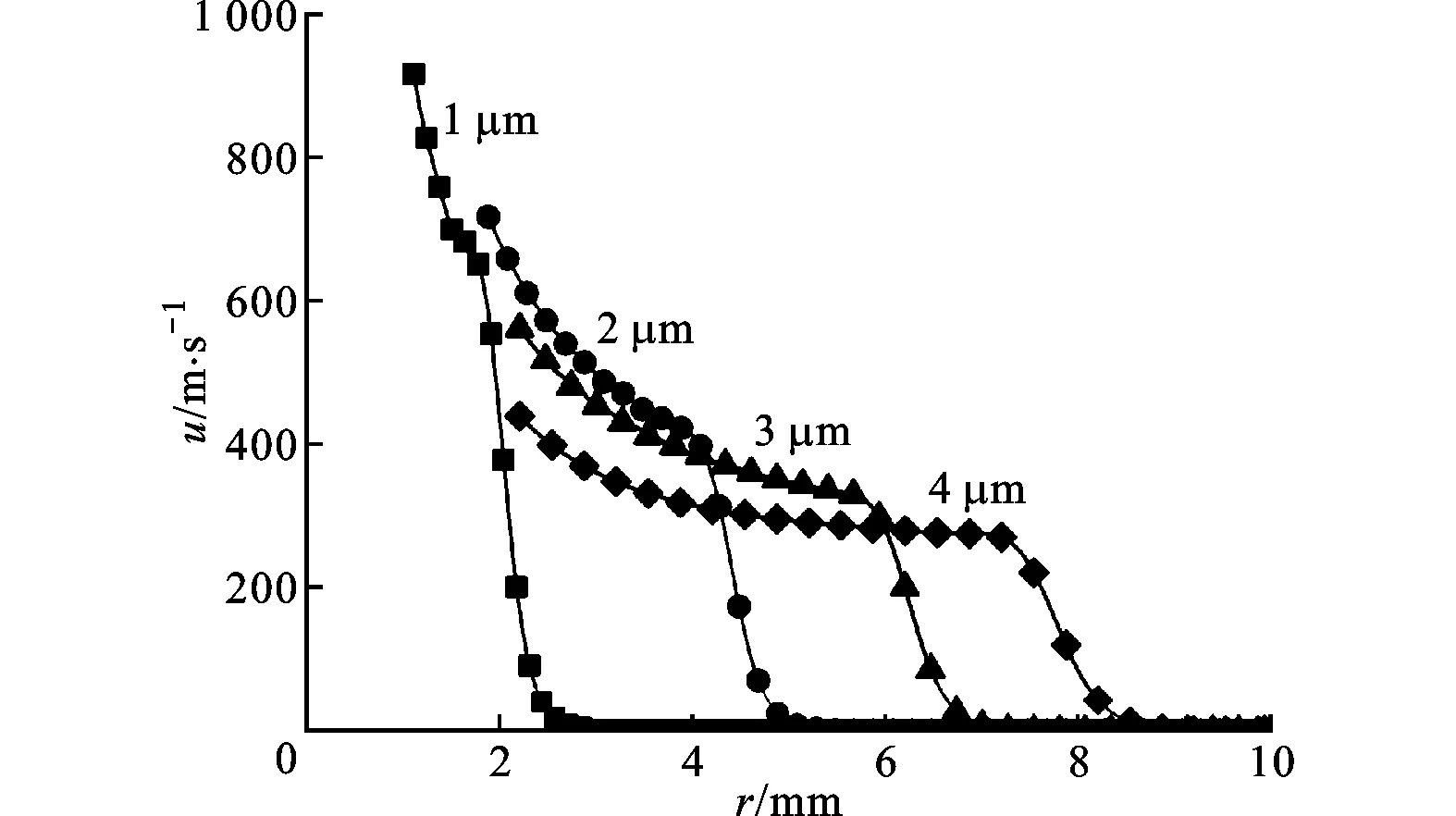
图7 不同时刻的速度径向分布曲线

本文计算得到的冲击波前沿随时间传播轨迹与文献[8]的对比见图8,可以发现,在1 μs以前与2 μs以后,本文计算结果与实验值更加吻合。

图8 不同模型计算的冲击波前沿随时间变化曲线

2.3 冲击波在水介质中的传播特性

图9显示了计算得到的距放电通道中心100 mm处冲击波压强时间历程曲线。从图中可见,冲击波波阵面于70 μs左右抵达,随后出现小幅振荡,并逐渐趋于稳定,这与文献[14]采用PCB-138A38压力传感器测到的冲击波典型波形图类似。

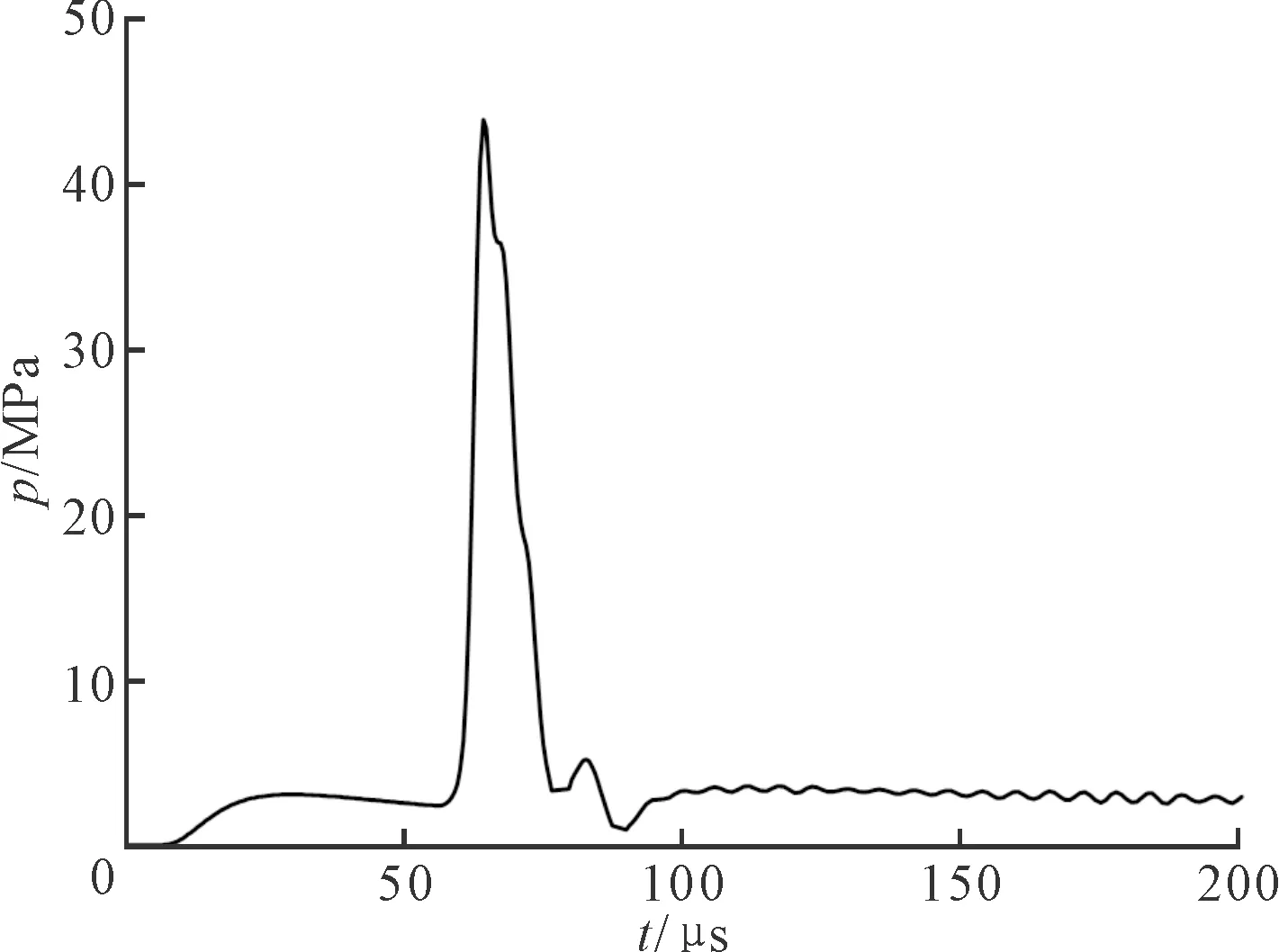
图9 计算得到的典型冲击波压强时间历程曲线

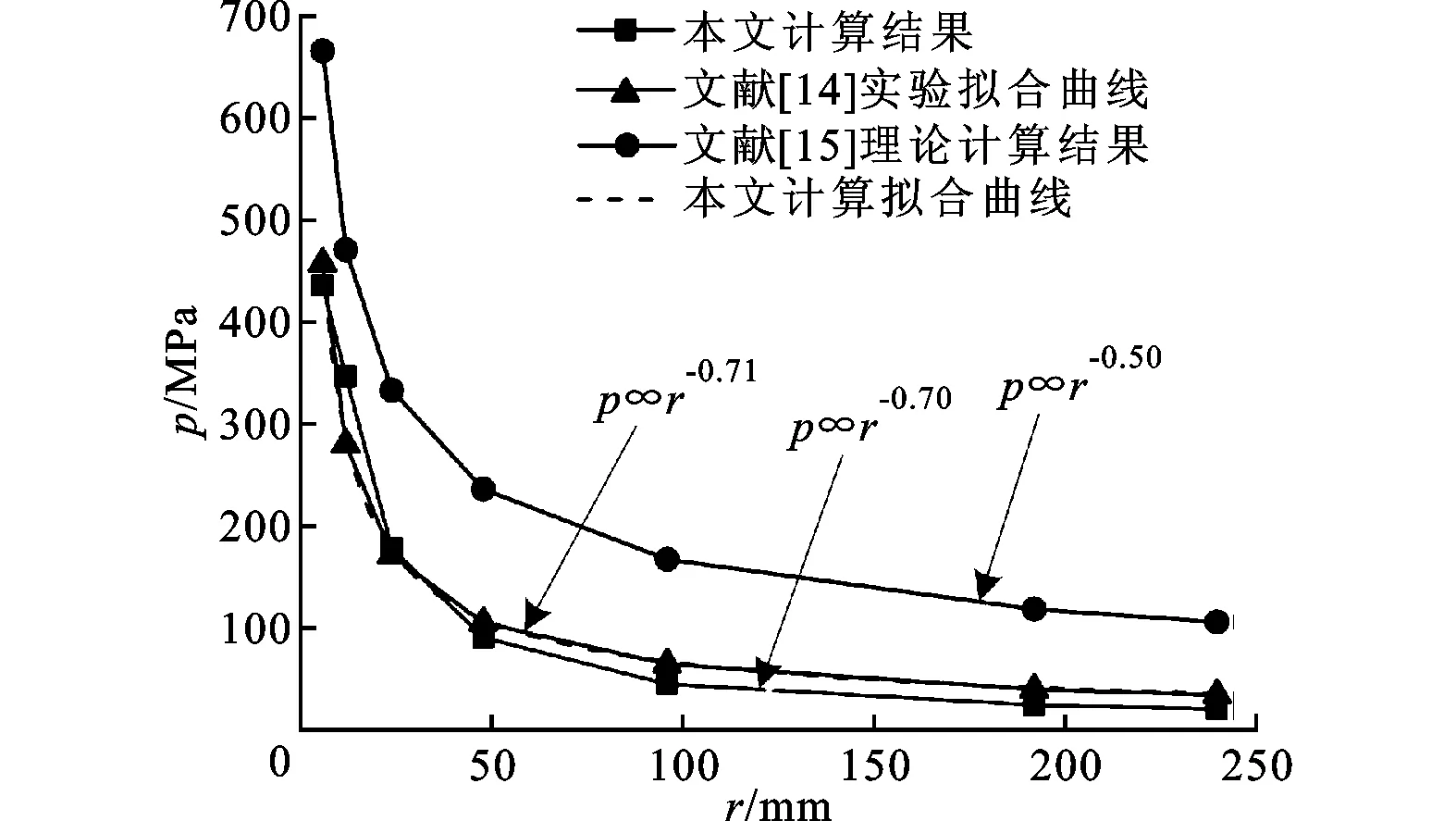
图10 冲击波压强随传播距离变化曲线

不同计算模型与文献实验值得到的冲击波压强随传播距离变化曲线见图10,可以看到,冲击波压强峰值随径向传播距离增加衰减较快,通过对不同距离压强计算值的拟合,本文计算得到的压强峰值与径向距离满足r-0.70传播规律。值得注意的是,文献[14]通过采用不同测量方法获得了距离电爆炸丝中心不同距离的冲击波幅值,并对实验结果进行了拟合,得到冲击波随距离衰减幂数为-0.71,进一步验证了本文计算模型的有效性。图10也给出了文献[15]根据理论计算得到水中柱形冲击波传播过程压强和距离的关系。

3 结 论

本文对传统的基于活塞模型的冲击波传播模型进行了改进,引入了双人工黏性系数,建立了计算水中金属丝电爆炸冲击波产生与传播过程的一维流体力学模型。

(1)与无人工黏性系数法及单人工黏性系数法相比,双人工黏性系数法使计算结果与实际冲击波物理参数的分布更为接近。

(2)本文模型可计算等离子体放电通道与冲击波波阵面之间水介质的物理参数、冲击波前沿传播轨迹、冲击波时间历程曲线,并且可以估计放电等离子通道壁的压强。

(3)获得了冲击波强度P随着径向距离r的衰减规律,即P∞r-0.70。

(4)采用一维流体力学模型计算电爆炸冲击波的产生与传播规律,不涉及脉冲放电条件下等离子体的复杂演变过程,也不涉及放电通道与水之间的复杂物理化学过程,只需根据诊断实验得到放电通道膨胀轨迹,就可以模拟水中金属丝电爆炸冲击波的产生与传播过程,计算得到的放电通道与波阵面之间水介质物理参数的空间分布也可以用来估算能量传输效率等。

[1]CHO C, CHOI Y W, KANG C, et al.Effects of the medium on synthesis of nanopowders by wire explosion process [J].Applied Physics Letters, 2007, 91(14):141501.

[2]TKACHENKO S I, ROMANOVA V M, MINGALEEV A R, et al.Study of plasma parameter’s distribution upon electrical wire explosion [J].European Physical Journal:D, 2009, 54(2):335-341.

[3]朱隽, 江孝国, 陈楠.用于温密物质研究的强流电子束加载技术 [J].强激光与粒子束, 2013(1):99-103.ZHU Jun, JIANG Xiaoguo, CHEN Nan.High intensity electron beam as a tool for warm dense matter studies [J].High Power Laser and Particle Beam, 2013(1):99-103.

[4]GRINENKO A, GUROVICH V T, KRASIK Y E, et al.Addressing water vaporization in the vicinity of an exploding wire [J].Journal of Applied Physics, 2006, 100(11):113309.

[5]GRINENKO A, SAYAPIN A, GUROVICH V T, et al.Underwater electrical explosion of a Cu wire [J].Journal of Applied Physics, 2005, 97(2):023303.

[6]SHEFTMAN D, SHAFER D, EFIMOV S, et al.Evaluation of electrical conductivity of Cu and Al through sub microsecond underwater electrical wire explosion [J].Physics of Plasmas, 2012, 19(3):034501.

[7]ORESHKIN V I, CHAIKOVSKY S A, RATAKHIN N A, et al.“Water bath” effect during the electrical underwater wire explosion [J].Physics of Plasmas, 2007, 14(10):102703.

[8]VEKSLER D, SAYAPIN A, EFIMOV S, et al.Characterization of different wire configurations in underwater electrical explosion [J].IEEE Transactions on Plasma Science, 2009, 37(1):88-98.

[9]张鸣远, 景思睿, 李国君.高等工程流体力学 [M].西安:西安交通大学出版社, 2006:335.

[10]LASTMAN G J, WENTZELL R A.Comparison of five models of spherical bubble response in an inviscid compressible liquid [J].The Journal of the Acoustical Society of America, 1981, 69(3):638-642.

[11]汤文辉.冲击波物理 [M].北京:科学出版社, 2011:104.

[12]VONNEUMANN J, RICHTMYER R D.A method for the numerical calculation of hydrodynamic shocks [J].Journal of Applied Physics, 1950, 21(3):232-237.

[13]FEDOTOV-GEFEN A, EFIMOV S, GILBURD L, et al.Generation of a 400 GPa pressure in water using converging strong shock waves [J].Physics of Plasmas, 2011, 18(6):062701.

[14]SAYAPIN A, GRINENKO A, EFIMOV S, et al.Comparison of different methods of measurement of pressure of underwater shock waves generated by electrical discharge [J].Shock Waves, 2006, 15(2):73-80.

[15]LANDAU L D, LIFSHITZ E M.Fluid mechanics [M].2nd ed.Oxford UK:Pergamon Press, 1987:271-273.

(编辑 杜秀杰)

One-Dimensional Simulation for Shock Waves Generated by Underwater Electrical Wire Explosion

LI Xingwen,CHAO Youchuang,WU Jian,JIA Shenli,QIU Aici

(State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China)

To understand the formation mechanism of the shock waves (SWs) generated by underwater electrical wire explosion (UEWE), double artificial viscosities are introduced to establish one-dimensional simulation model for SWs by UEWE based on classic piston model and similarity parameter method.In this simulation the trajectory of the discharge plasma channel (DPC) boundary serves as the unique input parameter, water pressure and SW velocity versus the distance from exploding wire and the period from exploding moment are obtained.The calculated results are compared with the experimental values from the other literatures to confirm the validity.The SWs calculated with double artificial viscosities method coincide well with the practical situation.At the explosion beginning the SW pressure reaches the grade of GPa at the DPC boundary, the obtained pressure amplitudes of SWs are found to be in direct proportion to the -0.7 power of radial propagation distance.The calculating method does not involve the complicated processes of pulse discharge, physical changes of DPC, and physical-chemistry interaction between DPC and water, only the DPC boundary trajectory obtained by experimental diagnostics is taken to simulate the generation and propagation processes of SWs generated by UEWE.

underwater discharge; electrical wire explosion; shock waves; artificial viscosity; plasma

2014-07-15。 作者简介:李兴文(1978—),男,教授。 基金项目:国家“863计划”资助项目(2013AA064502)。

时间:2014-10-31

http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.013.html

10.7652/xjtuxb201504001

TM89

A

0253-987X(2015)04-0001-05