水下目标多元声传感阵列网络定位方法

吴杰,冯祖仁,刘恒,刘江

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安工业大学电子信息工程学院, 710032,西安;3.西安机电信息技术研究所引信动态特性国防科技重点实验室,710065,西安; 4.中国重型机械研究院有限公司,710032,西安)



水下目标多元声传感阵列网络定位方法

吴杰1,2,冯祖仁1,刘恒3,刘江4

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安工业大学电子信息工程学院, 710032,西安;3.西安机电信息技术研究所引信动态特性国防科技重点实验室,710065,西安; 4.中国重型机械研究院有限公司,710032,西安)

针对由于环境干扰因素等影响水下目标精确定位的问题,提出了采用以声传感器为核心的多五元声传感阵列网络定位方法。根据水下空间环境,建立了多五元声传感阵列网络定位空间数学模型,研究与分析网络结构的多五元声传感阵列定位算法,给出了水下目标多五元声传感阵列网络定位参数的计算式及误差分析。分析表明:多五元声传感阵列网络定位参数的精度与声传感器阵列的布阵方式和声传感器之间的时延密切相关,随着时延的增大,水下目标方位角、俯仰角及距离误差也增大;通过采用单五元声传感阵列定位算法和多五元声传感阵列网络定位模拟对比实验,在同一区域下,多五元声传感阵列网络定位算法测量误差小于单五元声传感阵列定位算法测量误差,验证了水下目标多五元声传感阵列网络定位具有测试精度高的优点,为水下目标的精确定位及精确制导研制提供了技术方法,为开拓水下目标检测奠定了基础,具有很高的应用价值。

水下目标;声定位;多五元声传感阵列网络;误差分析

水下目标定位建立在水声定位系统的基础之上,水声定位系统是利用水下声波实现对目标定位的系统,简称为水声定位系统[1]。该系统依赖于声传感器网络,利用声沿着不同距离路径传播时到达声传感器的时间差或者相位差等信息,来实现对水中目标的定位[2-3]。为了精确获得水下目标位置及运动轨迹,常采用声传感器阵列网络[4],利用声传感器网络的空间几何关系进行定位。一般而言,声阵列传感器的分布可分为线阵、面阵和立体阵。对于固定式阵列,线阵定位算法是最简单的。线阵是由布设在一条直线上的若干个声传感器组成,用于对半个平面进行定位的常用阵型,这种方法只能对以线阵列所在直线为界的半个平面进行定位,否则没有唯一的解[5];面阵声传感器阵列是将传感器布置在一个平面上,它可以对整个平面的目标进行探测与定位,也可以对以阵列所在的平面为界的半个空间进行定位,但是对于水下的空间不确定轨迹,存在着误差较大的缺点[6];立体声阵列传感器定位技术是在三维立体空间布置声传感器[7],可以对整个空间进行定位,但是由于所使用的传感器较多,并且传感器之间的几何关系也较为复杂,因此单独采用立体声阵列传感器进行定位时算法较为复杂。在不同的探测环境以及精度要求的条件下,对于目标的定位所选取的阵列排布形式也就不同。大量资料表明,立体声阵列传感器相比于其他的阵列有更优的性能。为了改善立体声阵列传感器计算复杂的缺陷,本文研究一种改进的多五元声定位探测技术及其误差分析。

1 多五元声传感阵列网络的目标定位方法

五元空间目标声探测定位结构原理如图1所示,其中S0、S1、S2、S3以及S4是声探测阵的探测传感器单元(或称基元),由于探测阵进行三维空间目标定位时位置是相对位置,因此需要选择相应的基准点,选择S0作为基准点,将其看作坐标系的原点,其余点距离坐标轴的距离均为D。S1与S2在xoy平面,S3与S4在zoy平面,4个元的坐标(xi,yi,zi)(i=1,2,3,4)分别为(D,0,D)、(-D,0,D)、(0,-D,-D)以及(0,D,-D)。M为被测目标,设其坐标为(x,y,z),M点距离原点的距离为R,假设目标辐射的信号以球面波的形式向四周传播,目标的俯仰角为φ,方位角为γ,以目标辐射信号到S0的时间为基准,其他各个探测元接收到目标辐射信号的时差为Δti,ri0为声信号到达第i个探测接收元的声程差(同样以S0为基准)。

图1 五元空间目标声探测定位结构原理

根据水下声波传播速度c,有

ri0=MSi-MS0=cΔti,i=1,2,3,4

(1)

根据图1的五元探测阵列目标探测结构原理,结合式(1)有

(2)

对式(2)进行迭代运算可解得

(3)

由于目标距离探测阵的距离R远远大于声程差,即R≫ri0,则式(3)可简化为

(4)

由式(4)可得

cosφ=z/R=(r20+r10-r30-r40)/4D=

(Δt2+Δt1-Δt3-Δt4)c/4D

(5)

tanγ=y/x=(r30-r40)/(r20-r10)=

(Δt3-Δt4)/(Δt2-Δt1)

(6)

R=4D2/[c(Δt2+Δt1+Δt3+Δt4)]-

[2(Δt2+Δt1+Δt3+Δt4)]

(7)

由上述的表达式可以得知目标M在以S0为原点的坐标系中的柱面坐标表达式为

(8)

式(8)即为目标在水下空间中的位置信息,通过式(8)可以对目标进行定位,即目标的声定位由方位角、俯仰角以及目标距离确定。

式(4)和(8)给出了单五元声定位的计算原理,对于广阔水下区域的目标位置,要想真正获得比较精准的位置定位,需要对其算法进行扩展与改进。依据测试水域的范围,可以建立网络状的声定位空间立体模型,按照每一个单元五元阵列结构,构建网络式的多五元声传感阵列网络定位模型,以满足不同区域的目标定位。假设在一定的水域范围,布置多个声传感器阵列,在图1模型的基础上,在距离第一组五元声传感阵列传感器中,在等间距离l沿着Y方向,布置多组五元声传感阵列传感器,如图2所示,ln为下一n组声传感阵列探测单元,若目标M任意坐标为(xn,yn,zn),M点距离原点的距离为Rn,目标的俯仰角为φn,方位角为γn,以目标辐射信号到S0n的时间为基准,其他各个探测元接收到目标辐射信号的时差为Δtin,ri0n为声信号到达第i个探测接收元的声程差。

图2 五元声阵列传感器网络结构示意图

在图2的基础上,按照各传感器阵列在水下布置的空间关系,可以建立五元声传感阵列传感器网络模型。按照图2的方式,获得以S0n为原点的坐标系中的柱面相对坐标表达式为

(9)

(10)

通过式(9)、式(10),按照获得的空间坐标及方位角、俯仰角以及目标距离,也可以获得水下目标运动轨迹。

2 水下目标定位误差分析及实验分析

根据五元空间目标声探测定位的网络结构算法,按照网络单元的目标方位角、俯仰角以及目标距离的表达式,可以从目标方位角、俯仰角以及目标距离来确定目标的位置。为了表述方便,用tin(i=1,2,3,4)分别替代4个时差表达式Δtin(i=1,2,3,4)。根据多五元声传感阵列网络定位计算模型,按照式(9)和式(10),对各参数进行误差分析。

2.1 俯仰角定位误差分析

-c/[16D2-c2(t1n+t2n-t3n-t4n)2]1/2

(11)

由俯仰角的表达式可知

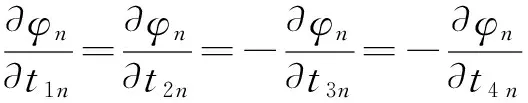
δφn=δ02c/(16D2-c2(t1n+t2n-t3n-t4n)2)-1/2

(12)

式中:δφn为某一位置点的俯仰角误差;δ0是声传感器的固有随机误差。

由式(12)可知,五元空间目标声探测定位的网络分布间距D、水下声场声速c以及时延都会对俯仰角的定位精度产生影响。随着D的增大,会使得俯仰角的定位误差减小,定位精度提高。另外,声传感器之间的时延对俯仰角的精度也有着很大影响[9]。

为了观察声传感器S1n、S2n的时延和与S3n、S4n的时延差对定位精度的影响,根据式(11)和式(12),计算获得定位俯仰角的误差分布如图3所示。

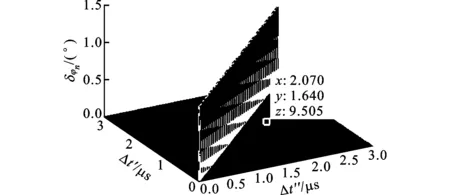
图3 俯仰角误差与时延差分布的关系

图3中,Δt′=Δt1n+Δt2n,Δt′为目标声信号到达声探测器S1n与S2n的时延差,Δt″=Δt3n+Δt4n,Δt″为声信号到达声探测器S3n与S4n的时延差。当两个时延差相差0.43 μs时,此时的俯仰角误差很小,当两者差距很小时,例如在0.02 μs时,俯仰角的误差快速增大。因此,为了使得俯仰角的误差小,应该使得两个时延差较大。在实际测量中,若Δt1n+Δt2n与Δt3n+Δt4n之间的差较大,那么测得的俯仰角的精度高,误差也越小。

2.2 方位角定位误差分析

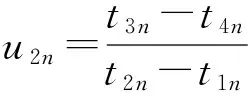
(13)

同理,有

(t4n-t3n)/[(t2n-t1n)2+(t3n-t4n)2]

(14)

由方位角的表达式可知

(15)

δγn为方位角误差。由式(15)可知,除了声探测器自身的误差外,主要的误差来源还是时延对系统方位角的误差影响较大,当|Δt′|=|Δt2n-Δt1n|越小,同时|Δt″|=|Δt3n-Δt4n|也越小时,系统测量的方位角误差较大。为了对比|Δt2n-Δt1n|与|Δt3n-Δt4n|对系统方位角的影响,通过计算获得的方位角误差分布如图4所示。

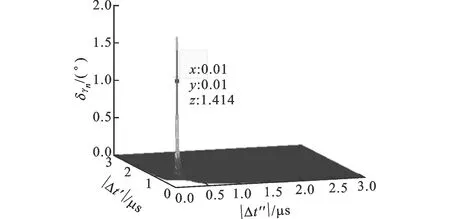
图4 时延差与方位角误差分布的关系

从图3可知,在多五元声传感器阵列探测定位网络模型中的声传感器S1n和S2n,它们的时延差|Δt2n-Δt1n|和声传感器S3n、S4n的时延差|Δt3n-Δt4n|对方位角δγn精度的影响是,当两个传感器的时延差数值都较大时,方位角的估计精度就会增大。对图4中坐标为(0.01,0.01,1.414)的目标点,当两个时延差都为0.01 μs时,方位角的定位精度为1.414°。因此,为了提高方位角的定位精度,|Δt1n-Δt2n|与|Δt3n-Δt4n|中,任有一个较大即可满足要求。同时,为了消除误差,可以对传感器的信号处理进行相应的识别处理,以获得多声传感器之间的高精度时间差。

2.3 目标距离定位误差分析

由式(10),可得误差表示式为

(16)

根据式(16)可知,4个时延对目标距离的影响相同。在对俯仰角及其方位角定位误差分析的基础上,若想提高对目标距离估计的精度,则需要时延值之和较大。通过计算获得的目标距离误差分布如图5所示。

图5 水下声场声速以及声传感器间距与目标定位距离误差分布的关系

由图5可知,当声速一定时,声传感器的间距对定位精度的影响不明显,这是由于间距的较小变化,相对于水下声速较大范围的变化而言不是特别明显。当D一定时,定位误差会随着声速的变化而快速变化,这说明在实验中对于水下声场声速的估计十分重要,当不同地区的声场声速变化时,若不予以考虑,那么对于距离的估计将会产生很大的影响[11],因此应该重视水下声场声速的变化。

2.4 实验分析

为了验证采用的多五元声传感阵列网络定位算法的高精度和可行性,建立在实验室的深水环境采用统一坐标系,将空间目标定位的方位角、俯仰角以及目标距离反演到目标实际位置坐标来计算与实验验证,分别布置了单一的五元声传感阵列定位测试系统(如图1所示)和多五元声传感阵列网络定位测试系统(如图2所示),分别对5个固定已知目标进行定位验证,通过两种系统所测坐标与固有目标已知位置对比来衡量。5个固定已知目标的位置分布为(0.5 m,0 m,0.5 m)、(0.5 m,0.5 m,0.5 m)、(1.0 m,0 m,1.0 m)、(1.5 m,0.5 m,1.5 m)、(2.5 m,1.0 m,2.5 m)。设单一的五元声传感阵列定位测试系统和多五元声传感阵列网络定位测试系统测量的目标位置分别采用(xs,ys,zs)和(xw,yw,zw),单位均为m。按照5个固定已知目标位置,模拟目标在动态下发出的声信号功率不同,获得了两组数据,见表1、表2。

由表1和表2可见,采用两种状态下的目标声信号进行测试, 发现采用单五元声传感阵列定位测试系统获得的数据与目标固定的已知位置误差偏大,特别是在小功率目标声信号状态下,说明了测试系统的延迟误差与目标发出的声功率有关。在目标声信号强的状态下,声传感器对传播的声信号识别比较灵敏,有利于信息提取,输出的信号边缘更陡,使得传感器之间的计时值精度得到提高,定位精度也得到提高,但是在同一目标声功率条件下,多五元声传感阵列网络定位测试系统的定位精度优于单五元声传感阵列定位测试系统。

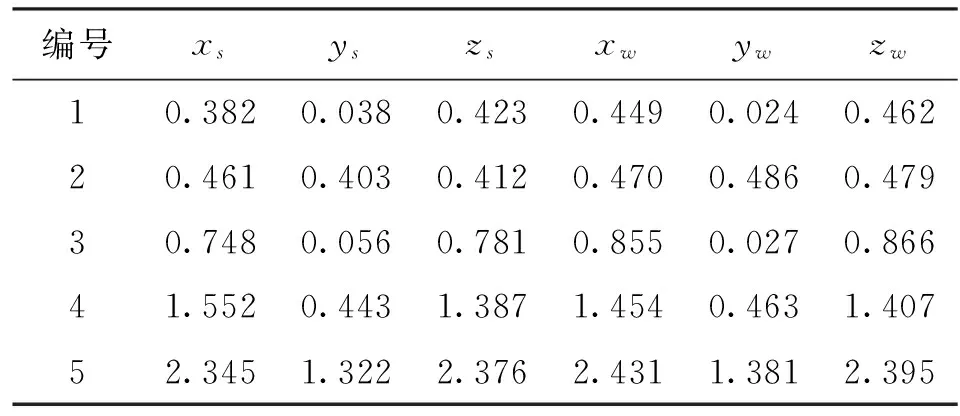
表1 模拟目标发出45 dB声信号实验数据 m

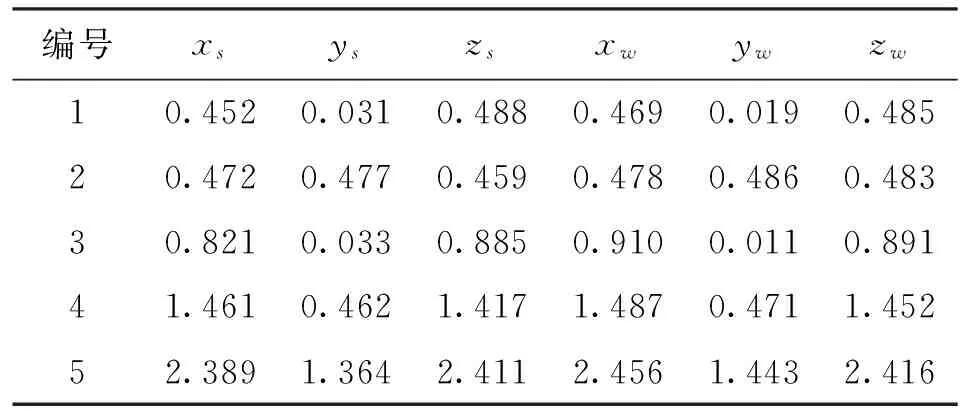
表2 模拟目标发出65 dB声信号实验数据 m

3 结 论

水下目标定位是海洋水下探测研究内容之一,为了很好地掌握水下目标的动态轨迹,需要知道水下目标的具体位置,为此本文在水下声传感阵列探测基础上,建立了通过五元声定位的基本模型,开展了多五元声传感阵列的目标网络式定位算法研究,给出推理过程并对相应的参数进行了误差分析。结果表明:多五元声传感阵列网络定位参数的精度与声传感器阵的布阵方式和声传感器之间的时延密切相关,随着传感器之间的时延差增大,水下目标方位角、俯仰角及距离误差也增大。这说明要提高定位精度,在设计过程中需要对多元网络式的声传感器之间的输出目标信息提取处理,以减少时延差。本文的计算模型和理论误差计算方法,给工程实践设计提供了理论计算与设计依据,具有很高的工程应用价值。同时,本文还给出了模拟环境下的实验及测试数据,通过对比的方式,验证了所建立模型的正确性和科学性。由于理论仅是在模拟环境下的研究测试,对大海洋环境水下测试还需要进一步研究与探讨。本文的算法和误差分析,为进一步研究水下目标定位方法提供了重要分析依据,具有较高的实践价值。

[1]章新华, 张晓明, 林良骥.船舶辐射噪声的混沌现象研究 [J].声学学报, 1998, 23(2):134-140.ZHANG Xinhua, ZHANG Xiaoming, LIN Liangji.Researches on chaotic phenomena of noises radiated from ships [J].Acta Acustica, 1998, 23(2):134-140.

[2]李建, 孙贵青, 张春华, 等.阵间模基处理被动定位技术研究 [J].声学技术, 2013, 32(2):86-91.LI Jian, SUN Guiqing, ZHANG Chunhua, et al.Passive location using inter-array model-based processing [J].Technical Acoustics, 2013, 32(2):86-91.

[3]LI Hanshan, WANG Zemin, GAO Junchai, et al.Analysis and calculation object detection capture rate in multi-sky-screens across measurement system [J].Optik, 2014, 124(20):4369-4373.

[4]SONG H C, HODGKISS W S, KUPERMAN W A, et al.Experimental demonstration of adaptive reverberation nulling using time reversal [J].Journal of Acoustical Society of America, 2005, 118(3):1381-1387.

[5]LI Hanshan.Research on a new photoelectric detection method to anti-muzzle’s flame or light disturbance and projectile’s information recognition in photoelectric detection target [J].Optoelectronics and Advanced Materials:Rapid Communications, 2014, 8(7/8):653-658.

[6]DOWLING D R.Phase-conjugate array focusing in a moving medium [J].Journal of Acoustical Society of America, 1993, 94(3):1716-1718.

[7]HO K C, CHAN Y T.An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis [J].IEEE Transactions on Signal Processing, 2006, 54(3):809-822.

[8]刘翔, 宋常建, 胡磊.一种非视距环境下的椭圆-双曲线混合被动定位技术 [J].电路与系统学报, 2013, 18(2):305-309.LIU Xiang, SONG Changjian, HU Lei.A new hybrid ellipse-hyperbola locating technology in NLOS environment [J].Journal of Circuits and Systems, 2013, 18(2):305-309.

[9]ABADI S H, ROUSEFF D, DOWLING D R.Blind deconvolution for robust signal estimation and approximate source localization [J].Journal of Acoustical Society of America, 2012, 131(4):2599-2610.

[10]李建龙, 祝恒年, 赵航芳, 等.基于时反算子分解的时反髙分辨率定位技术研究 [J].声学学报, 2009, 34(1):60-66.LI Jianlong, ZHU Hengnian, ZHAO Hangfang, et al.Study of time reversal highly resolved localization by decomposition of the time reversal operator [J].Acta Acustica, 2009, 34(1):60-66.

[11]惠俊英, 马敬广, 李峰, 等.二元阵被动时间反转镜定位技术研究 [J].哈尔滨工程大学学报, 2013, 28(11):1247-1251.HUI Junying, MA Jingguang, LI Feng, et al.Passive localization technology using time reversal with a two-sensor array [J].Journal of Harbin Engineering University, 2013, 28(11):1247-1251.

[本刊相关文献链接]

李昕,张永,殷德民,等.采用紧束缚格林函数法研究原子吸附石墨烯纳米带电子输运.2015,49(2):37-42.[doi:10.7652/xjtuxb201502007]

丁正龙,徐月同,傅建中.深孔内径的在线精密测量原理及系统.2015,49(1):65-71.[doi:10.7652/xjtuxb201501001]

赵建华,张陵,孙清.利用粒子群算法的传感器优化布置及结构损伤识别研究.2015,49(1):79-85.[doi:10.7652/xjtuxb 201501013]

郭军军,元向辉,韩崇昭.采用熵函数法的多传感器空间配准算法的研究.2014,48(11):128-134.[doi:10.7652/xjtuxb 201411022]

赵建伟,贾维敏,姚敏立,等.移动卫星通信系统组合姿态估计算法.2014,48(8):36-41.[doi:10.7652/xjtuxb201408007]

魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法.2014,48(6):1-6.[doi:10.7652/xjtuxb 201406001]

王书民,张爱武,胡少兴,等.采用光学成像法的航空稳定平台振动幅度检测.2014,48(6):25-30.[doi:10.7652/xjtuxb 201406005]

连峰,马冬冬,韩崇昭.扩展目标联合检测与估计的误差界.2014,48(4):8-14.[doi:10.7652/xjtuxb201404002]

韩玉兰,朱洪艳,韩崇昭,等.多扩展目标的高斯混合概率假设密度滤波器.2014,48(4):95-101.[doi:10.7652/xjtuxb 201404017]

高锐,李赞,司江勃,等.一种双重序贯检测的协作频谱感知方法.2014,48(4):102-108.[doi:10.7652/xjtuxb201404018]

宋渤,徐龙起,张桂铭,等.采用微传感器的黏/密度实验系统及其性能测试.2014,48(3):44-48.[doi:10.7652/xjtuxb 201403009]

周秦武,隋芳芳,白平,等.嵌入式无接触视频心率检测方法.2013,47(12):55-60.[doi:10.7652/xjtuxb201312010]

(编辑 武红江)

A Network Localization Method with Multi-Acoustic Sensor Array for Underwater Target

WU Jie1,2,FENG Zuren1,LIU Heng3,LIU Jiang4

(1.School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.School of Electronic Information Engineering, Xi’an Technological University, Xi’an 710032, China; 3.National Defense Laboratory of Science and Technology for Dynamic Characteristics of Fuze, Xi’an Institute of Electromechanical Information Technology, Xi’an 710065, China; 4.China National Heavy Machinery Research Institute Corporation, Xi’an 710032, China)

A network localization algorithm with multiple five-element acoustic sensor arrays is proposed to solve the precise orientation of underwater targets, which is affected by environmental disturbance, and acoustic sensors are used as the core.A multiple five-element arrays acoustic sensor localization model is build based upon the underwater spatial relationships.A calculation formula of the spatial location of underwater targets and error analysis are given by studying and analyzing the multiple five-element arrays acoustic sensor localization algorithm of network structure.The analysis results show that the accuracy of positioning parameters of the multiple five-element arrays acoustic sensor localization algorithm is related to the disposal way of acoustic sensor array and the time delay among the acoustic sensors.The azimuth, pitch angle and distance errors of the underwater target increase as the time delay increases.Simulation and comparison in the same area between the single five-element array acoustic sensor localization algorithm and the multiple five-element arrays acoustic sensor localization algorithm show that the measurement error of the multiple five-element arrays acoustic sensor localization algorithm is smaller than that of the single five-element array acoustic sensor localization algorithm.The result verifies advantage of the multiple five-element arrays acoustic localization algorithm, that is, its test accuracy is excellent.The algorithm provides a technical method for the precise orientation of underwater targets and the design of precision-guided munition, and lays a foundation for the detection of underwater targets.

underwater target; acoustic localization; multiple five-element acoustic sensor array network; error analysis

2014-10-14。 作者简介:吴杰(1979—),男,博士生;冯祖仁(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61105126,61203350,61271362);国防重点实验室基金资助项目(9140C360202130C36130);陕西省教育厅专项科研计划资助项目(2014JK1336)。

时间:2015-03-04

http:∥www.cnki.net/kcms/detail/61.1069.T.20150304.1641.001.html

10.7652/xjtuxb201504007

TP391.4

A

0253-987X(2015)04-0040-06