一种鲁棒的稀疏信号重构算法

郝雯洁,齐春

(西安交通大学电子与信息工程学院,710049,西安)



一种鲁棒的稀疏信号重构算法

郝雯洁,齐春

(西安交通大学电子与信息工程学院,710049,西安)

针对稀疏信号重构性能不稳定的问题,结合半阈值迭代算法,提出了一种鲁棒的稀疏信号重构算法。该算法首先对随机信号采用半阈值迭代算法进行重构,以获得初步的重构信号,然后改变迭代初值和参数初值进行新的迭代计算,同时增加一个新的循环终止条件,在保证算法稳定性与收敛速度的同时,使迭代结果跳出相对误差较大的局部极小点而收敛于误差较小的点成为可能,提高了重构信号的成功率。对该算法进行了信号重构和图像重构2个方面的实验,结果表明,与半阈值算法及相关算法比较,无论是对高斯信号、符号信号还是自然图像信号,该算法重构信号的成功率都有明显提高,较半阈值算法平均提高了约30%～40%,表现出较强的鲁棒性。

稀疏信号;重构;鲁棒;局部极小点

近年来,随着科学技术的快速发展,高分辨率图像采集的要求越来越高,需要处理的数据量以极大的速度在增加,这给信号处理的能力提出了更高的要求。信号的稀疏表示理论越来越引起人们的广泛关注和研究[1-3],而快速稳健的稀疏信号重构算法对该理论的应用发展起着至关重要的作用,目前已发展了多种算法。文献[4]提出的匹配追踪(MP)算法,通过在过完备库中自适应地选取能够表达信号局部特性的时频原子,最终将信号表示为时频原子的线性组合,但由于该算法所选原子具有非正交性,因而其收敛速度慢。正交匹配追踪(OMP)算法[5]对MP算法进行了改进,通过对已选择原子集合进行正交化以保证迭代的最优性,从而减少迭代次数。随后提出的规则化正交匹配追踪(ROMP)算法[6]、压缩采样匹配追踪(CoSaMP)算法[7]等都有不同程度的改进,得到了更好的稀疏信号重构效果。

2012年,由徐宗本等人提出了基于l1/2范数的半阈值迭代算法[8],相比基于l1范数最小化的算法,该方法具有所需观测点数少、运算速度快等特点,因此极具研究价值,但在实际应用中,该算法的信号重构性能并不稳定,有些信号不能得到成功重构。本文对文献[8]算法进行了进一步研究和改进,提出了一种鲁棒的稀疏信号重构算法,通过改变迭代初值和更新参数初值,在保证算法稳定性和收敛速度的同时,使重构信号跳出相对误差较大的局部极小点成为可能;同时,根据收敛性判断公式,增加了新的循环终止条件,对误差进一步约束,通过多次循环迭代,使算法收敛于误差较小的点,将半阈值算法不能重构的信号成功重构,提高了重构信号的成功率,获得了更好的稀疏信号重构能力。

1 半阈值迭代算法

1.1 信号的稀疏表示

设有一长度为N的信号x∈RN,A是一个M×N的观测矩阵,并且M≪N,观测值y=Ax是一个M维向量,则信号的重建可表示为

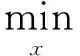
‖x‖0s.t.y=Ax

(1)

即利用观测向量y通过求解该优化问题来重构原信号。然而,式(1)是NP难的,很难用现有的优化算法得到求解。进一步研究发现,由于信号是稀疏的,当观测矩阵满足限制等距条件(restricted isometry property,RIP)[9]时,信号就可能由观测值精确重构,并指出可将其转化为等效的l1范数凸集优化问题[1]进行求解,即

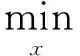
‖x‖1s.t.y=Ax

(2)

1.2 半阈值迭代算法

虽然l1范数最小化为凸优化问题易于求解,但实际应用中发现,该方法得到的解并不是最优的[10-11]。为此,Xu等人通过使用一种相位图的处理方法研究发现,运用l1/2范数代替l1范数求解最优化问题可产生更加稀疏的解[8],于是提出了半阈值迭代算法的基本模型[12]

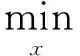
‖x‖1/2s.t.y=Ax

(3)

然而,式(3)是一个非凸优化问题,很难用一种高效的算法来求解。结合有关非凸优化问题的一些解决方法[11,13],文献[12]通过使用阈值迭代算法求解该问题,推导得出其表达式

xn=H(B(xn-1))

(4)

B(xn-1)=xn-1+μAT(y-Axn-1)

(5)

式中:H(x)=(h(x1),h(x2),…,h(xN))T为由半阈值函数h导出的半阈值算子,其表达式为

h(xn)=

(6)

式中

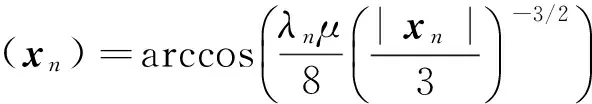
(7)

(8)

(9)

(10)

其中,[B(xn)]S+1是B(xn)按照由大到小排列后的第S+1个。算法以x0=0为迭代初值,通过不断迭代直至满足|xn-xn-1|<ε条件时迭代终止,得到重构信号。

2 鲁棒的稀疏信号重构算法

半阈值迭代算法是一种有效的信号重构算法,已得到广泛的应用[14-16]。然而,非凸优化问题可能存在多个局部极小点,该算法仅能保证收敛于某一局部极小点[17],当陷入一个相对误差较大的局部极小点时,迭代终止条件|xn-xn-1|<ε也可能得到满足,但此时并未成功重构信号,从而影响了信号重构的成功率。针对上述问题,本文提出了一种鲁棒的稀疏信号重构算法。算法的具体步骤如下:

(1)参数初始化,x0=0,根据式(5)、(8)～(10)计算参数初值B(x0)、μ、λ0、t0;

(2)运用半阈值迭代算法获得重构信号xn;

(3)根据式(5)计算B(xn);

(4)判断迭代结果是否满足新的循环终止条件

|B(xn)-xn|<ε

(11)

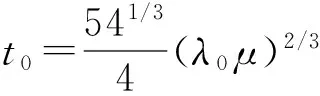
(6)返回步骤(2),直到算法迭代结果满足式(11)。

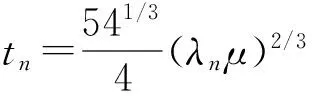
虽然改变了迭代初值使算法跳出局部极小点成为可能,但由于半阈值算法的迭代终止条件|xn-xn-1|<ε只能使迭代结果收敛于某一局部极小点,并不能保证恢复得到原稀疏信号,因此本文算法在此基础上增加了新的循环终止条件|B(xn)-xn|<ε。为了进一步说明该终止条件的作用,引入条件数的概念,条件数是指线性方程y=Ax的解对y中误差或不确定度的敏感性的度量。定义矩阵A的条件数等于A的范数与A的逆的范数的乘积,即cond(A)=‖A‖‖A-1‖, 由于B(xn) =xn+μAT·

(y-Axn)(式(5)),将式(5)代入式(11)得到

|μAT(y-Axn)|<ε

(12)

另外,对于Axn=y-r在等式两边同时左乘A的逆矩阵,可得xn=A-1(y-r)(r为误差),以及x*=A-1y(x*为真值),因此可以得到误差向量

‖e‖=‖x*-xn‖=‖A-1r‖≤‖A-1‖‖r‖

(13)

同时得到观测值‖y‖=‖Ax*‖≤‖A‖‖x*‖,进一步推导可得

(14)

结合式(13)、(14)可以得到

(15)

由于条件数总是大于1的,因此‖y-Axn‖小的扰动可能会造成‖x*-xn‖形成较大的误差。通常情况下,真值是未知的,为了尽量减小真值与所得值的误差,对‖y-Axn‖进行约束,使误差e保持在一个较小的范围内,从而得到相对误差较小的重构信号,提高算法重构信号的成功率。

为了验证本文算法的有效性,对大量的随机稀疏信号进行实验。为了方便叙述,本文将一次改变迭代初值进行迭代计算得到重构信号称为一次循环,将信号长度(即信号点数)用N表示。图1给出了运用本文算法多次循环对信号进行重构的分步结果图。可以看出,第1次循环即运用半阈值算法所得到的重构信号与原稀疏信号的差异很大,很多点处的信号值都没有得到成功重构,而运用本文算法随着循环次数的增多,重构得到的信号与原信号的差异逐渐减小,在第6次循环结束后,成功重构信号。为了定量分析本文算法的性能, 表1给出了5组不同随机稀疏信号每次循环得到的重构信号与原稀疏信号的均方误差(MSE)值。从表1中的数据可以看出,第1次循环得到的重构信号均方误差值较大,此时认为信号没有成功重构,而运用本文算法,经过多次循环迭代后,最终得到均方误差值很小的信号,即本文算法将半阈值算法不能重构的信号成功重构。

(a)第1次循环(Half算法) (b)第2次循环 (c)第3次循环

(d)第4次循环 (e)第5次循环 (f)第6次循环图1 本文算法多次循环重构信号的分步结果图

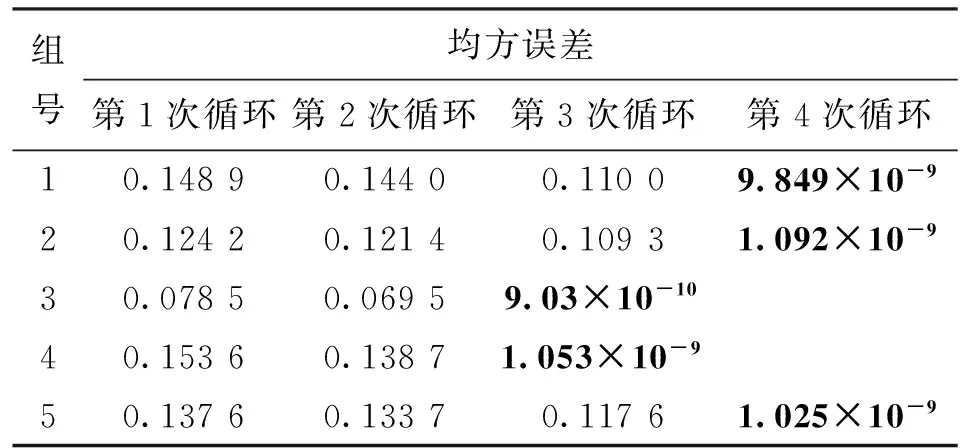
表1 信号重构分步均方误差值

注:黑体数据为符合要求的重构信号。

3 实验结果及分析

为了验证本文算法的有效性,进行了信号重构和图像重构2个方面的实验,并与一些信号重构的主流算法进行对比,如硬阈值迭代算法(IHT)[18]、正交匹配追踪算法(OMP)[5]、规则化正交匹配追踪算法(ROMP)[6]、压缩采样匹配追踪算法(CoSaMP)[7]等。通过大量的实验数据分析比较来评价算法的性能。

3.1 信号重构实验

实验使用长度N=256、稀疏度S从1到100连续变化的随机高斯信号和随机符号信号2种稀疏信号来模拟可能遇到的信号,即信号非零元素的幅值分别服从正态分布和1,-1分布。实验所用的观测矩阵为高斯随机矩阵,满足RIP条件,观测点数M=130,使用原信号与重构信号的均方误差值(MSE)作为判决条件,门限值取为10-4,为了保证实验结果的可靠性,本文进行了1 000次重复实验,运用成功重构信号的概率来评价算法的性能。

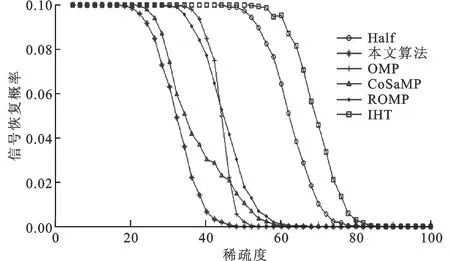
(a)随机高斯信号

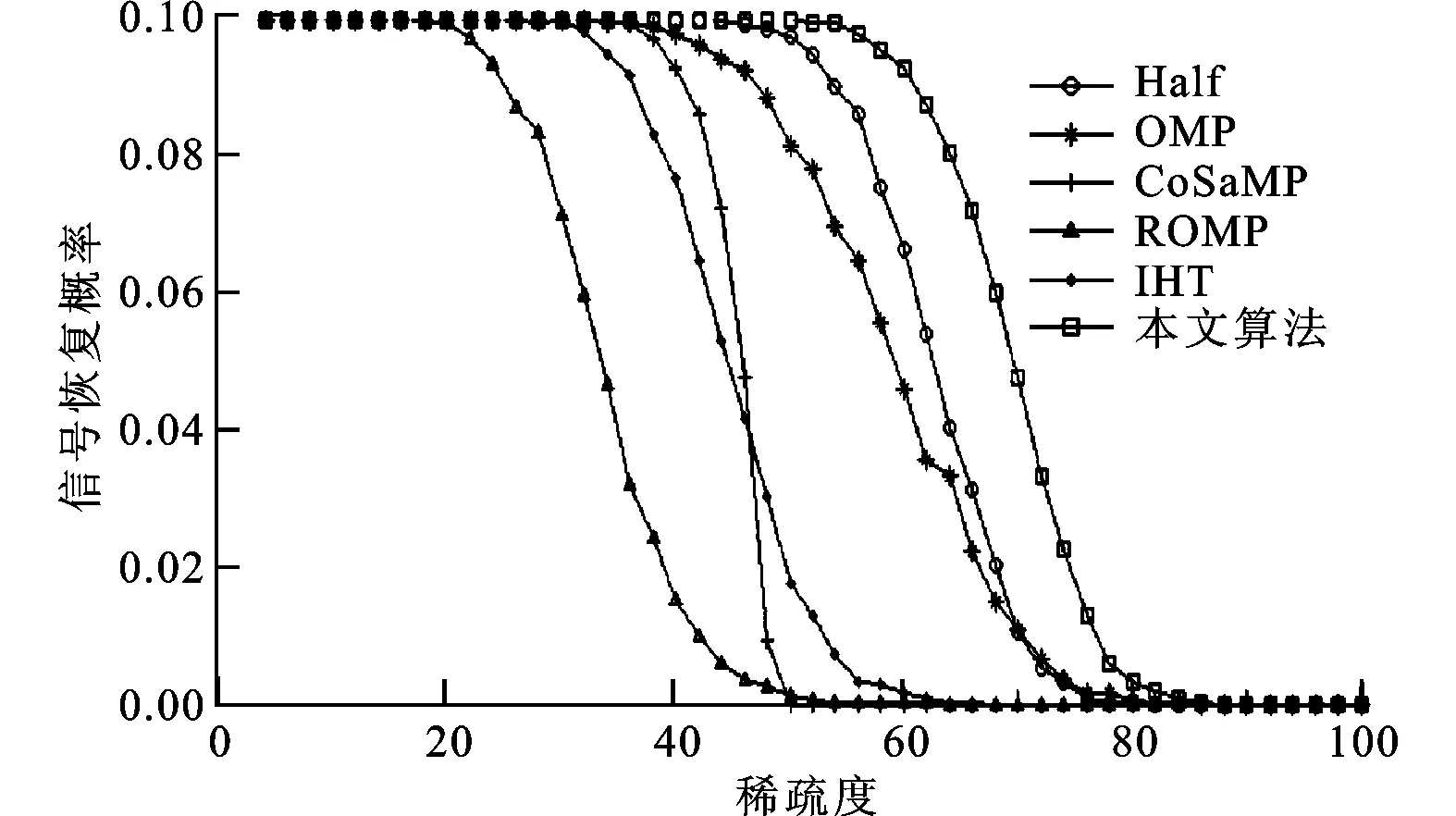
(b)随机符号信号图2 几种算法对不同稀疏度信号的重构成功率

几种不同算法在固定观测点数情况下对不同稀疏度信号的重构成功率情况如图2所示,可以看出,随着稀疏度的增加,各算法的性能均有所下降,半阈值迭代算法在各算法中的信号重构成功率较高,而本文算法相比半阈值算法性能又有了明显的提高,信号重构成功率平均提高了约30%～40%,并且大多数算法对随机符号信号重构时性能明显下降,而本文算法的性能基本保持不变,体现了较强的鲁棒性。

3.2 图像重构实验

实验使用一幅64×64像素的Shepp-Logan大脑图进行仿真实验,首先对该图像进行4层小波分解,得到N为4 096、稀疏度为723的稀疏信号,再运用几种算法在不同观测点数情况下对信号进行重构,最后将重构信号进行小波逆变换得到重构图像。实验结果如表2所示。为了定量分析本文算法重构图像的性能,表3给出了表2重构图像的峰值信噪比RPSN值。

由表2的实验结果可以看出,在观测点数较多的情况下,6种算法都能够得到较好的重构图像,随着观测点数的减少,重构图像逐渐模糊;从表3的数据中清楚地看出,当观测点数下降到1 600时,各算法的性能都迅速下降,只有本文算法的重构图像仍保持着较高的RPSN值,可见在观测点数较少的情况下,本文算法的优势更为突出,相比半阈值算法重构图像的RPSN值有了明显的提高,具有较强的图像重构能力。

表2 6种算法在不同观测点数情况下的重构图像

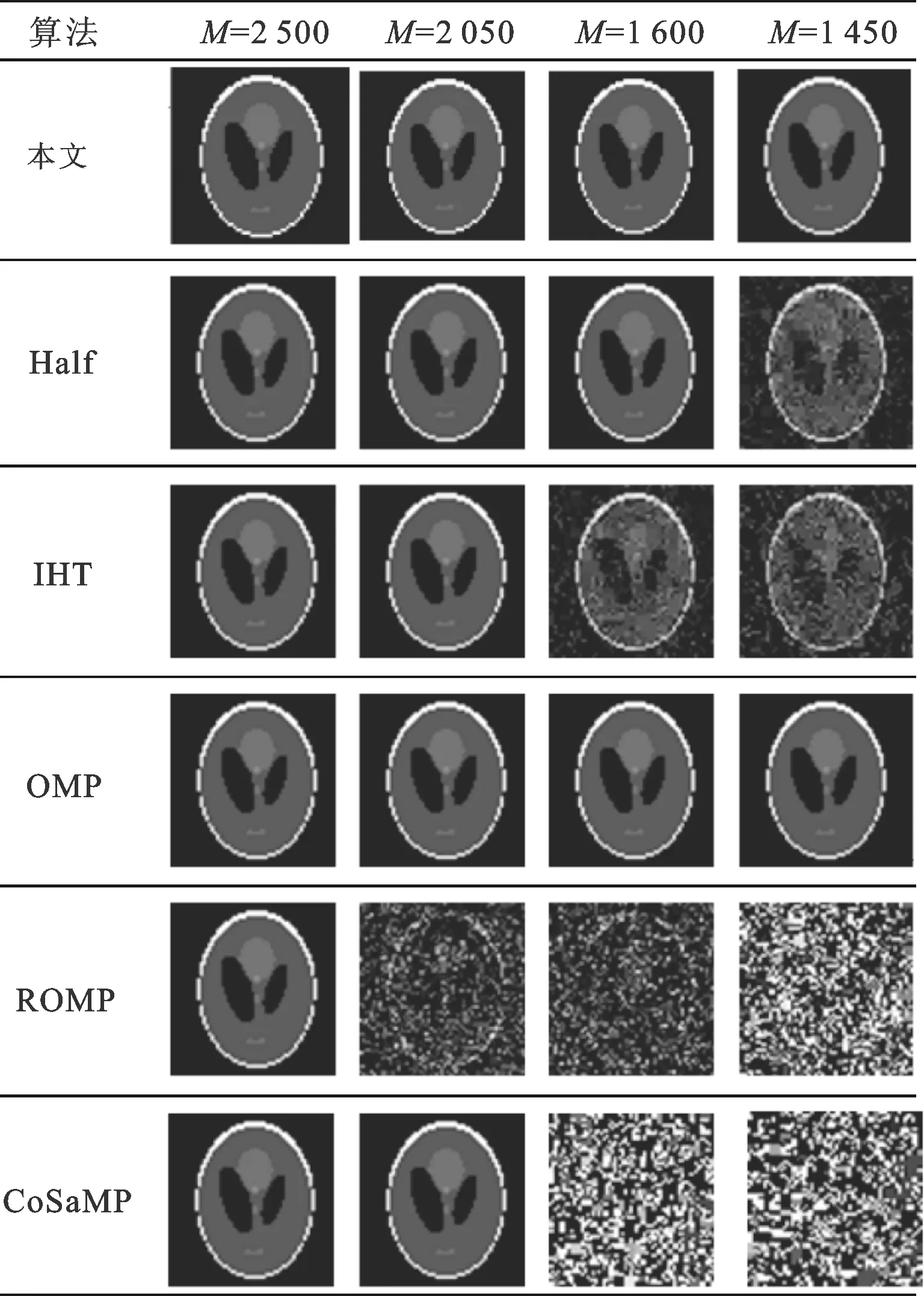
表3 不同采样率下6种算法重构图像的峰值信噪比

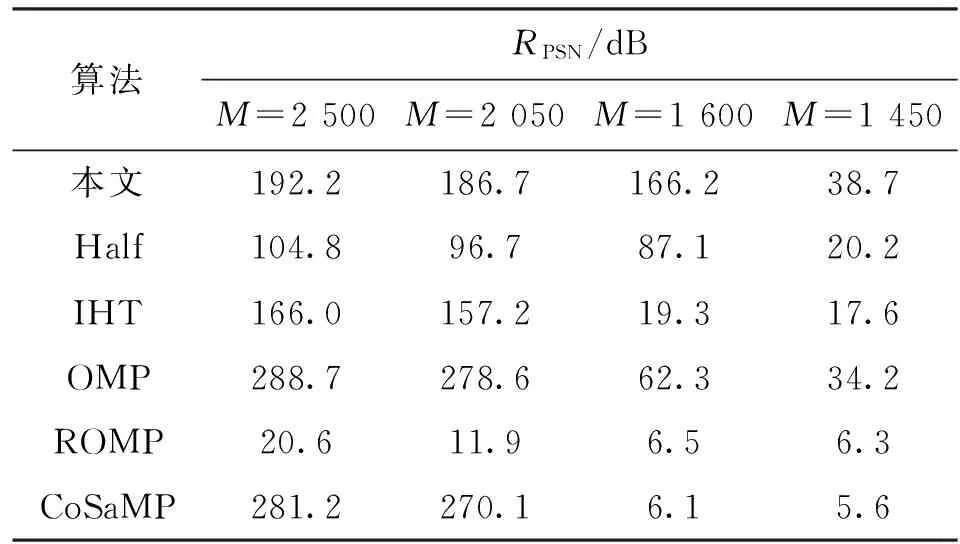
算法RPSN/dBM=2500M=2050M=1600M=1450本文192.2186.7166.238.7Half104.896.787.120.2IHT166.0157.219.317.6OMP288.7278.662.334.2ROMP20.611.96.56.3CoSaMP281.2270.16.15.6

4 结 论

针对稀疏信号重构性能不稳定的缺陷,本文提出了一种鲁棒的稀疏信号重构算法。通过改变半阈值迭代算法的迭代初值和更新参数,在保证算法稳定性和收敛速度的同时,使迭代结果跳出局部极小点成为可能;同时,提出了新的循环终止条件,使算法收敛于相对误差较小的点,将半阈值算法不能重构的信号成功重构,提高了算法重构信号的成功率。实验结果表明,相对比其他5种算法,本文算法重构信号的成功率有了明显提高,在观测点数较少的情况下仍能获得较清晰的重构图像,并且对于不同种类的信号,本文算法均能获得较好的效果,表现出较强的鲁棒性。

[1]CANDES E, WAKIN M, BOYD S.Enhancing sparsity by reweightedL1minimization [J].Fourier Analysis and Applications, 2008, 14(5):877-905.

[2]MALIOUTOV D M, CETIN M, WILLSKY A S.A sparse signal reconstruction perspective for source localization with sensor arrays [J].IEEE Transactions on Signal Processing, 2005, 53(8):3010-3022.

[3]史金刚, 齐春.一种双约束稀疏模型图像修复算法 [J].西安交通大学学报, 2012, 46(2):6-11.SHI Jingang, QI Chun.An image inpainting algorithm based on sparse modeling with double constraints [J].Journal of Xi’an Jiaotong University, 2012, 46(2):6-11.

[4]MALLAT S G, ZHANG Z.Matching pursuits with time-frequency dictionaries [J].IEEE Transactions on Signal Processing, 1993, 41(12):3397-3415.

[5]TROPP J A, GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit [J].IEEE Transactions on Information Theory, 2007, 53(12):4655-4666.

[6]NEEDELL D, VERSHYNIN R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit [J].Foundations of Computational Mathematics, 2009, 9(3):317-334.

[7]NEEDELL D, TROPP J A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples [J].Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.

[8]XU Zongben, GUO Hailiang, WANG Yao, et al.Representative ofL1/2regularization amongLq(0

[9]CANDES E J, ROMBERG J, TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory, 2006, 52(2):48.

[10]杨扬, 刘哲, 吕方园.一种迭代加权l1范数的信号优化恢复方法 [J].计算机工程与应用, 2010, 46(3):128-130.YANG Yang, LIU Zhe, LV Fangyuan.Signal recovery based on iterative weightedl1norm [J].Computer Engineering and Applications, 2010, 46(3):128-130.

[11]桂丽华, 徐兵, 崔永福.基于lq最小化算法的稀疏信号分离 [J].通信技术, 2010, 43(8):84-86.GUI Lihua, XU Bing, CUI Yongfu.Sparse signal separation based onlqminimization [J].Communications Technology, 2010, 43(8):84-86.

[12]XU Zongben, CHANG Xiangyu, XU Fengmin, et al.L1/2regularization:a thresholding representation theory and a fast solver [J].IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(7):1013-1027.

[13]GASSO G, RAKOTOMAMONJY A, CANU S.Recovering sparse signals with a certain family of nonconvex penalties and DC programming [J].IEEE Transactions on Signal Processing, 2009, 57(12):4686-4698.

[14]QIAN Y T , JIA S, ZHOU J, et al.Hyperspectral unmixing viaL1/2sparsity-constrained matrix factorization [J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11):4282-4297.

[15]ZENG Jinshan, XU Zongben, ZHANG Bingchen, et al.AcceleratedL1/2regularization based SAR imaging via BCR and reduced Newton skills [J].Signal Processing, 2013, 93(7):1831-1844.

[16]XU Chen, PENG Zhiming, JING Wenfeng.Sparse kernel logistic regression based onL1/2regularization [J].Science China:Information Sciences, 2013, 56(4):1-16.

[17]ZENG Jinshan, LIN Shaobo, WANG Yao, et al.L1/2regularization:convergence of iterative half thresholding algorithm [J].IEEE Transactions on Signal Processing, 2014, 62(9):2317-2329.

[18]BLUMENSATH T, DAVIES M E.Iterative hard thresholding for compressed sensing [J].Applied and Computational Harmonic Analysis, 2009, 27(3):265-274.

(编辑 刘杨)

A Robust Reconstruction Algorithm for Sparse Signals

HAO Wenjie,QI Chun

(School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A robust reconstruction algorithm for sparse signals is proposed to focus on the problem that sparse signal reconstruction has unstable performance.Firstly, the signal is reconstructed by using the half thresholding algorithm.Then, initial value and initial parameters are changed to perform new iterations, and a new termination condition is applied, so that it is possible for the algorithm to escape from the local minima with large error, and the success rate of the signal reconstruction is improved.Experimental results of signal recovery and image reconstruction on Gaussian signals, sign signals and natural image signals show that the proposed algorithm increases the success rate of recovering signals, and its performance is better than that of the half thresholding algorithm and other competitive ones.Comparisons with the half thresholding algorithm show that the success rate of signal recovery of the proposed algorithm has an increase of 30%-40% in average with better robustness.

sparse signal; reconstruction; robust; local minima

2014-04-20。 作者简介:郝雯洁(1989—),女,硕士生;齐春(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(60972124);国家“863计划”资助项目(2009AA01Z321);教育部高等学校博士学科点专项科研基金资助项目(20110201110012)。

时间:2015-01-16

http:∥www.cnki.net/kcms/detail/61.1069.T.20150116.1510.003.html

10.7652/xjtuxb201504016

TN911.7

A

0253-987X(2015)04-0098-06