利用贝叶斯原理在隐私保护数据上进行分类的方法

杨攀,桂小林,安健,田丰,王刚

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安交通大学陕西省计算机网络 重点实验室,710049,西安;3.西安财经学院信息学院,710049,西安)



利用贝叶斯原理在隐私保护数据上进行分类的方法

杨攀1,2,桂小林1,2,安健1,2,田丰1,2,王刚3

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安交通大学陕西省计算机网络 重点实验室,710049,西安;3.西安财经学院信息学院,710049,西安)

针对可还原数据扰动(retrievable general additive data perturbation, RGADP)算法在保护数据库隐私时会影响数据挖掘结果的问题,提出一种利用贝叶斯原理在扰动数据上进行分类的方法。该方法分析RGADP算法过程,利用贝叶斯原理,根据扰动数据推算原始数据的概率分布,用估算的概率分布重构数据,并对重构数据进行分类以提高分类的正确性。实验结果表明:该方法估算出的概率分布与原始数据概率分布接近,且重构数据的分类正确率相比扰动数据而言平均可提高4%以上,其更接近原始数据的分类正确率,从而有效地降低了扰动算法对数据分类的影响;该方法的运行时间与数据量和数据分组数成正比,重构10 000条数据的运行时间在200 ms以内,因此该方法也具有较高的效率。

隐私保护;数据扰动;贝叶斯原理;分类

一直以来,数据发布共享与挖掘都是数据库的重要应用[1],它为科学研究、企业发展及人们生活均带来了诸多便利。近年来,诸如云计算等数据外包服务模式的迅猛发展,也为数据的发布和共享提供了更好的平台,但是数据发布后可能造成其中的敏感信息泄露,从而损害数据所有者的利益,因此隐私泄露问题已成为阻碍数据发布共享的主要因素。如何保护发布数据的隐私,并对其进行有效地挖掘成为学术界的研究热点。

数据匿名[2-3]是一种容易实现的抵抗身份泄露的隐私保护措施。通过将数据所有者的身份信息匿名化,可以防止攻击者将数据与个体直接对应,但是由于其他信息并没有隐藏,当攻击者获得足够多的背景知识后,仍可能识别出数据的所有者。密文检索[4]利用通常的加密策略来保护数据隐私,同时通过建立特殊的密文索引来支持对密文数据的检索,但是无法对密文数据做进一步分析。在对数据进行挖掘时,Kantarcioglu等提出针对关联规则的数据隐私保护方法[5],Vaidya等则在垂直分区的数据上提出针对K-means聚类算法的隐私保护方法[6]。此外,也有学者提出针对分类的隐私保护方法[7-8]。Muralidhar等则通过添加满足特定条件的噪声,提出能够保持原始数据统计特征不变的数据扰动算法(general additive data perturbation,GADP)[9-10]。

以上方法均以保护数据隐私为目的,分别适用于不同的数据处理应用。Yang等则考虑在云计算场景中授权用户对原始数据的访问需求[11],对GADP算法进行改进,提出可还原的GADP算法(RGADP),它具有更高的安全性,并支持数据所有者或授权用户利用密钥获取原始数据。RGADP算法能更好地适应云计算服务对数据隐私保护的需求,但扰动后的数据仍然只保证了数据的期望及协方差不变,并没有提供对数据挖掘的有效支持,限制了它在数据隐私保护中的应用。

针对扰动数据的挖掘问题,Ge等利用转移概率矩阵对扰动数据进行有效的决策树分类[12]。Li等提出一种改进的基于奇异值分解的扰动算法[13],并针对此算法提出相应的分类挖掘算法。Agrawal等利用贝叶斯原理估算原始数据概率分布[14],进而进行数据挖掘,可有效提高扰动数据的分类效果,但是只能处理简单的线性扰动数据,且每次只能估算一个属性。

本文采用与文献[14]相同的思路,针对RGADP算法扰动数据较大影响分类效果的问题,用扰动数据估算原始数据的概率分布,并基于此概率分布重构数据以进行分类,从而提高分类的正确性。通过分析RGADP算法的数据变换公式,结合贝叶斯原理,推导出从RGADP扰动数据估算原始数据概率分布的公式;RGADP扰动算法可对多个属性的数据同时进行变换,由此推导出的估算公式也可同时估算多个属性数据的概率分布;概率分布揭示了各属性值在各区间的分布情况,利用此分布重构数据,在重构数据上进行分类的准确率高于在扰动数据上进行分类,从而有效提高扰动数据的分类效果。

1 RGADP算法简介

RGADP算法将数据库U的属性分为隐私属性X及可公开属性S。S不包含隐私信息,无需变化。X是需要保护的信息,为表述方便,本文用到的符号及解释如表1所示。

表1 符号表

RGADP算法通过对X进行扰动变换得到Y来隐藏隐私信息,并使扰动后的数据U′保持期望及协方差不变,即

μU=μU′且ΣU=ΣU′

(1)

在RGADP算法中,对于给定的X和S,利用下式可生成满足式(1)的Y

Y=β0+Uβ1+ε

(2)

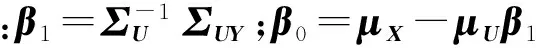
此外,ε为依照特定算法随机生成的噪声,满足

με=0且Σε=ΣX-ΣYUβ1

(3)

由上述步骤生成的Y满足

μY=β0+μUβ1+με=μX

(4)

(5)

这就保证了扰动后的数据期望和协方差与原始数据一致,即满足式(1)。

2 基于贝叶斯原理重构原始分布

在诸如贝叶斯及决策树等分类算法中,需要计算属性的概率,扰动后的数据已经破坏了原有的概率分布。文献[14]指出,利用贝叶斯原理,可以推导原始数据的近似概率分布,从而提高在扰动后数据上的分类效果。需要注意的是,这里只是估算原始数据的概率分布,而非原始值。因此,隐私信息仍然不会泄露。

文献[14]给出了一个在简单扰动数据上推导原始概率分布的过程,但由于其扰动算法只是独立地为每个属性添加噪声,与RGADP算法有较大不同,并不适用于本文。因此,本文分析RGADP算法中Y的生成过程,借鉴文献[14]的思想,计算在Y出现的情况下X的后验概率,以此作为原始数据X的概率分布。

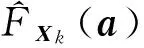
(6)

上式中Y的密度函数没有规律,无法有效表达,因此考虑更加规律的噪声数据的密度函数。首先需要分析噪声数据ε与X及Y的关系。

(7)

由此可知,该条记录添加的噪声为

εk=yk-β0-skβ11k-xkβ10k

(8)

将式(8)代入式(6)中,可得

(9)

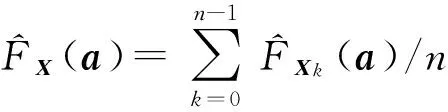
(10)

式(10)是本文估算X概率分布的主要依据,但为了真正实现对X概率分布的估算,还需做一些假设和改进。

2.1 噪声ε的概率密度

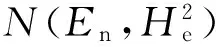
(11)

2.2 原始数据的离散化

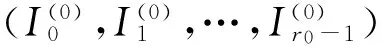
(12)

2.3 迭代法估算X的密度函数

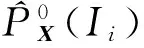
(13)

(14)

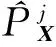
(15)

重构的复杂度主要取决于式(13)的计算复杂度以及迭代次数。在一次迭代中,对于每个Ii,式(13)的分母不变,只需计算一次,因此其实际计算复杂度为O(nr),而迭代次数则与具体数据集相关,可由实验进行观察,见4.3节。

3 基于重构的扰动数据分类

利用重构算法,可以通过扰动数据Y估算原始数据X在各个区域的概率分布,然后依照此分布重新生成数据X′,则X′与X具有相似的概率分布。X′与可公开的数据S构成新的用于分类的数据集Uc=[X′S]。至此,可以在Uc上进行分类处理。

在贝叶斯分类中需要计算后验概率,在决策树分类中需要使用诸如信息熵或Gini指标等来度量分裂点,这些操作都需要对训练集进行概率统计。由于Uc与U的概率分布相似,因此在Uc上进行的统计也比U′更接近原始值,从而可以提高分类效果。

需要注意的是,Uc与U只是整体概率分布相似,并不完全一致,而且以Uc为训练集,各个属性在各个类别上的概率值也会与U有差别,因此该方案可以提高在扰动数据上的分类效果,但是正确率一般不会超过原始数据。

对Uc分类得到的分类结果,可以作为原始数据的分析结果,供相关人员参考。此外,也可将分类器返回给数据所有者,以供其对其他未知类别的明文数据进行预测。

4 实验结果及分析

本节将通过实验测试重构算法,并利用UCI的数据集“Adult”[16]测试在重构数据集上的分类效果。实验主机配置为双核3.0 GHz主频的CPU及4 GB内存。

4.1 重构算法的效果

为检测重构的效果,首先利用RGADP算法对原始数据进行扰动变换,然后基于扰动后的数据估算原始数据的概率分布,对比原始数据、扰动数据与重构数据的概率分布。

(a)梯形分布

(b)双三角形分布图1 在模拟数据集上重构概率分布

如图1所示,首先模拟两种特殊的概率分布,图1a中原始数据的概率分布类似梯形,两头概率递增(减),中间概率均匀;图1b中则类似两个并列的三角形,有两次高峰。由图1可见,经RGADP算法扰动后的数据分布与原始数据有较大区别,而在该扰动数据上进行重构后,得到的概率分布则比较接近原始分布。

图2是在真实数据集Adult上进行的重构实验。首先,对属性age及fnlwgt利用RGADP算法进行扰动变换,然后基于扰动数据进行重构,对比原始数据、扰动数据与重构数据的概率分布。

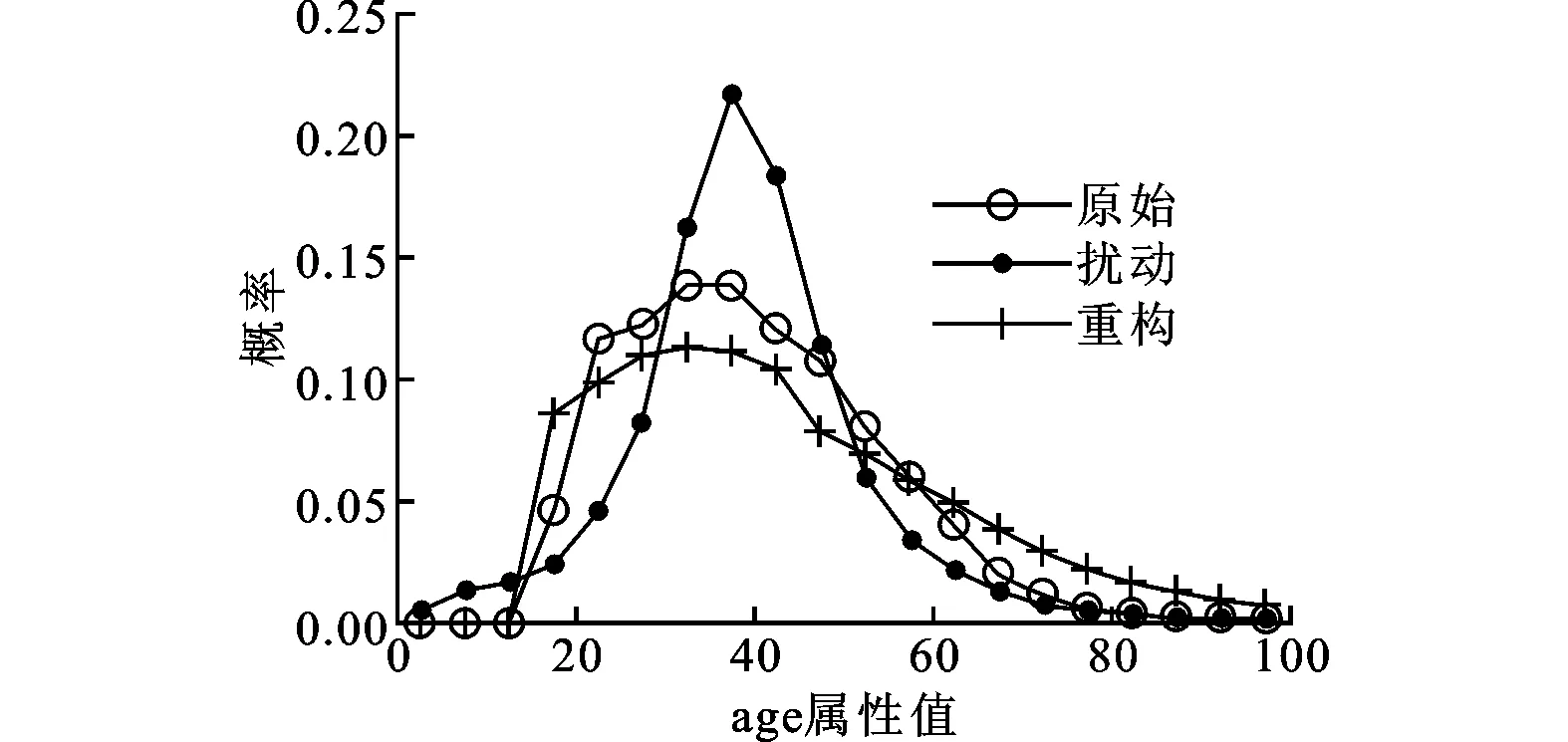
(a)age属性值的分布

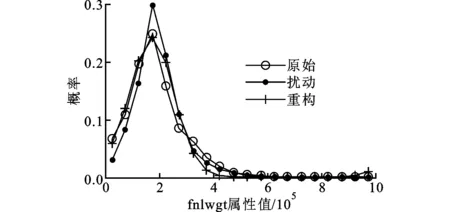
(b)fnlwgt属性值的分布图2 在真实数据集Adult上重构概率分布

由图2可见,原始数据和重构数据的概率分布十分相似。此外,在图2b中,由于RGADP算法保持数据的期望及协方差不变,而fnlwgt属性值相对集中在4×105范围内,因此扰动后数据的分布也与原始分布相似,但是重构的数据仍然更接近原始分布。可见,重构算法可以有效地估算原始数据的概率分布。

4.2 分类效果

以重构的数据为依据进行分类,以提高分类正确率是本文的最终目的,因此本节验证重构数据对分类效果的影响。

选择不同的分类算法及不同的分类属性,分别对原始数据、扰动数据及重构数据进行分类,并测试其分类的正确率,见表2。其中,DT、NB分别表示决策树和朴素贝叶斯分类算法,编号1表示所有属性参与分类,2表示去掉了小部分属性,3表示去掉了大部分属性。在上述各种分类策略中,始终保留age和fnlwgt属性。

同时,以文献[14]的算法作为参照。由于两种算法分别针对不同的扰动数据(生成扰动数据的扰动算法不同),因此我们只对比两种算法对扰动数据分类正确率的提高量,即重构数据正确率与扰动数据正确率之差,记为A。差值越大,说明算法能更好地减少扰动对分类的影响。表2中参照值是利用文献[14]的算法重构其所对应的扰动数据后,再计算分类正确率的提高量,记为R。

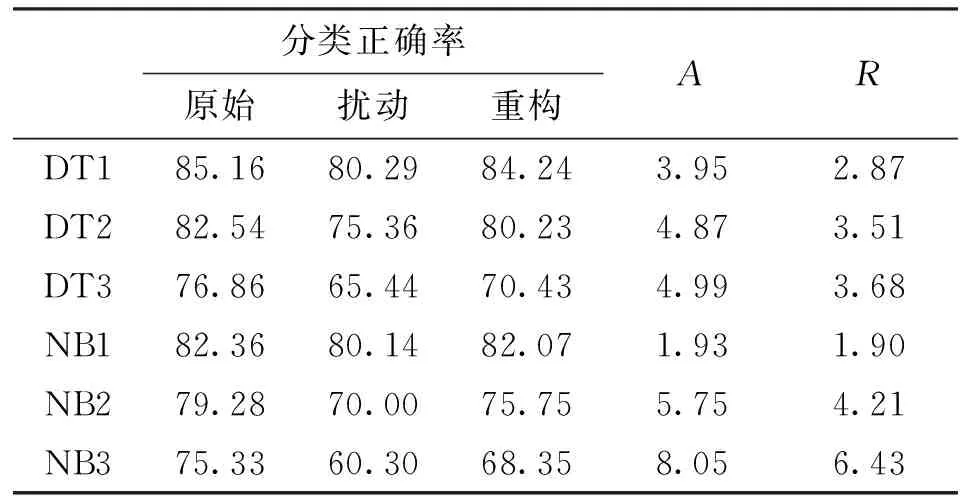
表2 分类的正确率及与参照算法的对比 %

由表2可知,当属性较多时,age与fnlwgt对分类结果的影响较小,因此变换(扰动或重构)后数据与原始数据的分类正确率接近。随着属性数量减少,age及fnlwgt对分类的影响开始变大,因而变换后数据对分类结果的影响也变大,导致正确率低于原始数据。

此外,在表2中,扰动数据的分类正确率在属性减少时大幅下降,而重构数据的正确率则明显高于扰动数据,因而重构数据可以有效降低扰动对分类的影响。由于本文算法是对多个属性统一进行估算,在一定程度上保留了不同属性间的相关性,因此与由文献[14]算法得出的参照值比较,本文算法能更有效地降低扰动对分类的影响。

4.3 重构的效率

虽然通过重构可以在扰动数据上分类,但重构本身也需要消耗时间,由2.3节分析可知,重构算法效率与数据量n及分组数r有关。本节中,分别对n与r设定不同的值,记录在不同的n或r值下,重构算法运行的时间。同样以文献[14]的算法作为参照。实验中有两个属性参与重构,文献[14]的算法需要分别对每个属性进行估算。其中,对于给定的分组数r,参照算法实际将两个属性分别分为r0、r1组,满足r=r0r1。实验结果如图3所示。

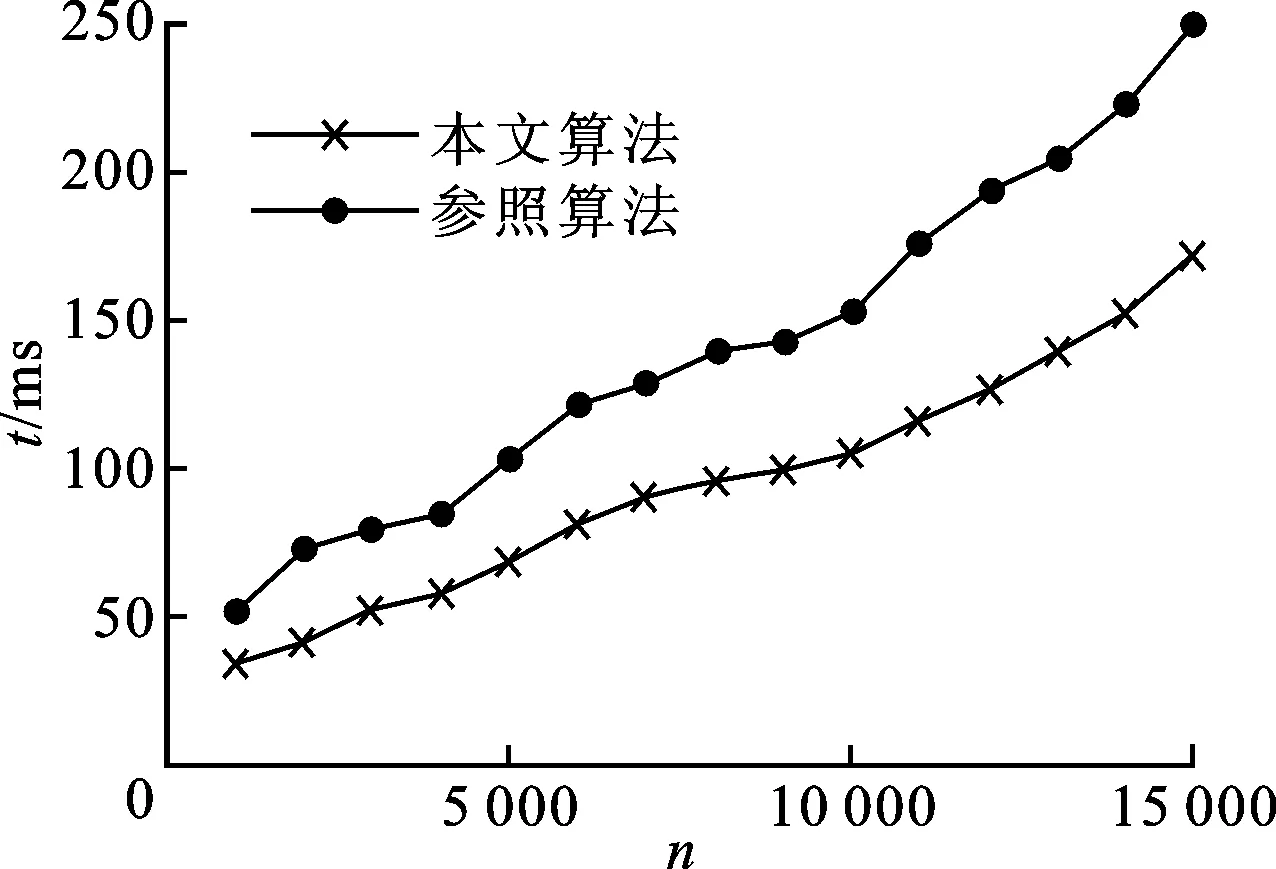
(a)r=200

(b)n=15 000图3 n及r对算法效率的影响

可见,随着n或r的增加,重构的时间也在增加。由于文献[14]的算法需要分别对每个属性进行估算,因此本文算法在r较少时效率更高,但是当r增加时,参照算法由于实际分组数较少,因而效率下降缓慢。相比而言,本文算法则随着r的增加,耗时也有明显增加。

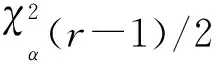
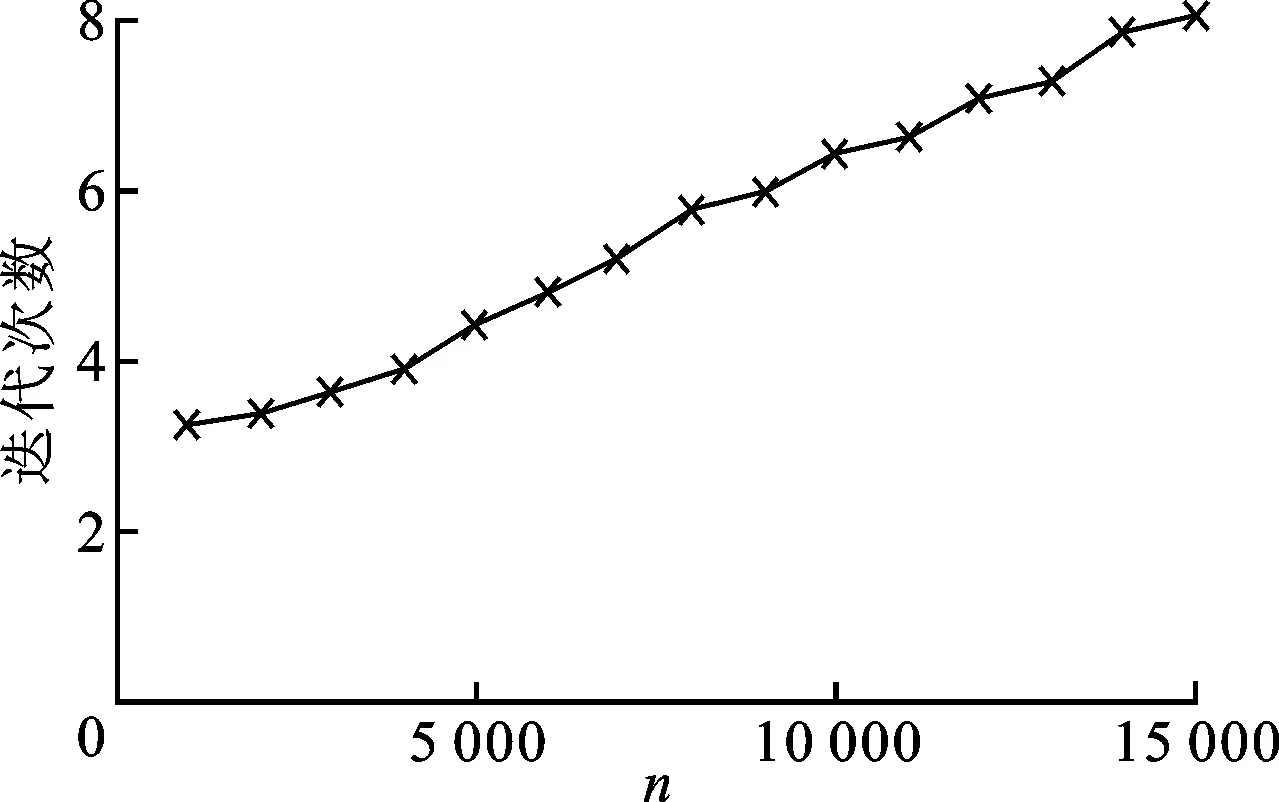
图4 数据量与迭代次数的关系

由实验可知,迭代次数会随着数据量的增加而缓慢增加,但是总体来讲,只需少量的迭代即可得到满足条件的概率分布。因此,可以认为我们的重构算法复杂度近似为O(nr)。

5 结 论

本文针对RGADP扰动数据影响分类效果的问题,利用贝叶斯原理重构原始数据的概率分布,并在重构数据上进行分类,以降低扰动对分类效果的影响,从而支持在扰动数据上的分类。为了提高重构效率,可以对扰动数据预先进行分组,以减少数据量,但却可能降低重构的效果,今后我们将进一步研究有效的分组策略。此外,如何根据扰动数据划分原始数据的各个区域也将是今后重点优化的内容。

[1]周水庚, 李丰, 陶宇飞, 等.面向数据库应用的隐私保护研究综述 [J].计算机学报, 2009, 32(5):847-861.ZHOU Shuigeng, LI Feng, TAO Yufei, et al.Privacy preservation in database applications:a survey [J].Chinese Journal of Computers, 2009, 32(5):847-861.

[2]SWEENEY L.K-anonymity:a model for protecting privacy [J].International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5):557-570.

[3]WANG S L, TSAI Z Z, TING I H, et al.K-anonymous path privacy on social graphs [J].Journal of Intelligent and Fuzzy Systems, 2014, 26(3):1191-1199.

[4]LI Jin, WANG Qian, WANG Cong, et al.Fuzzy keyword search over encrypted data in cloud computing [C]∥Proceedings of the 2010 IEEE International Conference on Computer Communications.Piscataway, NJ, USA:IEEE, 2010:1-5.

[5]KANTARCIOGLU M, CLIFTON C.Privacy-preserving distributed mining of association rules on horizontally partitioned data [J].IEEE Transactions on Knowledge and Data Engineering, 2004, 16(9):1026-1037.

[6]VAIDYA J, CLIFTON C.Privacy preserving k-means clustering over vertically partitioned data [C]∥Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA:ACM, 2003:206-215.

[7]张鹏, 唐世渭.朴素贝叶斯分类中的隐私保护方法研究 [J].计算机学报, 2007, 30(8):1267-1276.ZHANG Peng, TANG Shiwei.Privacy preserving naive Bayes classification [J].Chinese Journal of Computers, 2007, 30(8):1267-1276.

[8]BAGHEL R, DUTTA M.Privacy preserving classification by using modified C4.5 [C]∥Proceedings of the IEEE International Conference on Contemporary Computing.Piscataway, NJ, USA:IEEE, 2013:124-129.

[9]MURALIDHAR K, PARSA R, SARATHY R.A general additive data perturbation method for database security [J].Management Science, 1999, 45(10):1399-1415.

[10]MURALIDHAR K, SARATHY R.An enhanced data perturbation approach for small data sets [J].Decision Sciences, 2005, 36(3):513-529.

[11]YANG Pan, GUI Xiaolin, AN Jian, et al.A retrievable data perturbation method used in privacy-preserving in cloud computing [J].China Communications, 2014, 11(8):73-84.

[12]GE Weiping, WANG Wei, LI Xiaorong, et al.A privacy-preserving classification mining algorithm [C]∥Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining.Berlin, Germany:Springer, 2005:256-261.

[13]LI Guang, WANG Yadong.A privacy-preserving classification method based on singular value decomposition [J].International Arab Journal of Information Technology, 2012, 9(6):529-534.

[14]AGRAWAL R, SRIKANT R.Privacy-preserving data mining [J].ACM Sigmod Record, 2000, 29(2):439-450.

[15]LI Deyi, LIU Changyu, GAN Wenyan.A new cognitive model:cloud model [J].International Journal of Intelligent Systems, 2009, 24(3):357-375.

[16]KOHAVI R, BECKER B.UCI machine learning repository:adult data set [DB/OL].(1996-05-01) [2014-10-01].http:∥archive.ics.uci.edu/ml/datasets/Adult.

(编辑 武红江)

A Classification Method for Privacy-Preserved Data Using Bayesian Rule

YANG Pan1,2,GUI Xiaolin1,2,AN Jian1,2,TIAN Feng1,2,WANG Gang3

(1.School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.Shaanxi Province Key Laboratory of Computer Network, Xi’an Jiaotong University, Xi’an 710049, China; 3.School of Information, Xi’an University of Finance and Economics, Xi’an 710049, China)

A classification method for perturbed data using the Bayesian rule is presented to solve the problem that the result of data mining is affected when the retrievable general additive data perturbation (RGADP) algorithm is used to preserve privacy in database.The process of RGADP algorithm is analyzed, and the Bayesian rule is used to estimate the probability distribution of original data from the perturbed data.Then, new data are reconstructed from the estimated probability distribution and are classified to increase the accuracy of classification.Experimental results show that the probability distribution estimated by the proposed method is close to the original probability distribution.Comparison with the classification accuracy of perturbed data shows that the classification accuracy of the reconstructed data increases by more than 4% in average, and is closer to the original classification accuracy.Thus, the method can effectively reduce the effect of the perturbation algorithm on classification.Moreover, the running time of the method is proportional to the amount of data and the number of groups.The method costs less than 200 ms to reconstruct 10 thousands data, and has a high efficiency.

privacy-preservation; data perturbation; Bayesian rule; classification

2014-11-08。 作者简介:杨攀(1987—),男,博士生;桂小林(通信作者),男,教授,博士生导师。 基金项目:高等学校博士学科点专项科研基金资助项目(20120201110013);国家自然科学基金资助项目(61172090,61472316);中央高校基本科研业务费资助项目(XKJC2014008);陕西省科技统筹创新工程资助项目(2013SZS16)。

10.7652/xjtuxb201504008

TP301

A

0253-987X(2015)04-0046-07