射频隐身数据链的通信波形参数优化建模

谢桂辉,田茂,王正海,唐晓庆,李杰

(1.武汉大学电子信息学院,430072,武汉;2.中国西南电子技术研究所,610036,成都)



射频隐身数据链的通信波形参数优化建模

谢桂辉1,田茂1,王正海2,唐晓庆1,李杰1

(1.武汉大学电子信息学院,430072,武汉;2.中国西南电子技术研究所,610036,成都)

针对数据链在恶劣环境下被截获概率过高的问题,建立了一种基于射频隐身的通信波形参数优化模型。基于环境感知系统得到的通信距离和截获距离等先验知识,该优化模型以原始消息序列长度、编码码率、扩频因子、调制方式和波形分集度为优化参数,以指定距离的通信速率和被截获概率为优化目标,通过归一化和线性加权变换得到总优化目标,最后使用遍历法得到总优化目标的最大值并将对应的通信波形参数作为最优解。仿真结果表明:当载体信息安全等级提高时,优化模型在约束值范围内将通信速率适度降低,将被截获概率从原来的8.6×10-7降低至6.9×10-9;当数据链处于最恶劣的环境时,相同平均通信速率条件下优化后数据链的被截获概率可降低至优化前的1/1 000,大大提高了射频隐身性能。

数据链;射频隐身;通信波形参数;优化模型

随着无源探测系统探测距离的提高,装载了数据链的飞机或舰艇等设备平台面临的生存威胁越来越大。与传统材料隐身不同的是,射频隐身要求在保障系统通信性能的前提下尽可能提高隐身性能,因此,射频隐身已经成为一个重要研究领域[1]。

现有的大多数文献都是通过最大化信号不确定性[2]或最小化辐射能量[3-4]来实现射频隐身,这些文献相对于传统最大辐射功率法,其射频隐身性能已得到显著提高,但是它们都是基于固定的通信波形参数,无法使数据链在复杂环境下总以最合适的通信波形参数进行信号的辐射,存在一定的局限性。目前已有一些文献分析了通信波形参数对系统低截获特性的影响[5-10],但是仅考虑了单个通信波形设计技术的部分参数,没有对系统物理层波形设计技术进行整体联合分析,更没有涉及通信波形参数的优化问题。文献[11]针对多个通信波形参数对系统的通信速率进行了优化,但并未考虑射频隐身性能。因此,如何将通信波形参数与数据链的射频隐身需求结合起来,在射频隐身领域具有重要意义。

本文针对数据链射频隐身性能的通信波形参数的优化问题展开了研究:以原始消息序列长度、信道编码码率、扩频因子、调制方式和波形分集度为优化参数,以给定距离的被截获概率和可靠通信速率为优化目标,建立了一种自适应的通信波形参数优化模型。仿真结果表明,该优化模型可在不同的数据链载体信息类型和环境威胁因子下获得优化解。与优化前相比,优化后数据链在相同的通信速率下,可获得更低的被截获概率,具有较好的射频隐身性能。

1 多目标优化建模

1.1 通信速率模型

在质量随机变化的无线信道中,根据信道质量实时动态调整通信速率,是数据链通信系统高效传输载体信息的保障。通信速率可表示为

Rb=LQmC/ts

(1)

式中:L为原始消息序列长度;Qm为调制参数,当调制方式分别为BPSK、QPSK、16QAM时,Qm分别为1、2、4;ts为一个通信时隙持续时间;C为时域上的波形分集度,改变波形分集度可直接改变通信时隙内波形有效持续时间与静默时间的比例,这种通过改变辐射波形的占空比来调整通信系统通信速率的方式,已经应用于LINK16/LINK22等军用无线通信系统中[12]。

式(1)中数据链通信系统的通信速率受原始消息序列长度、调制方式和波形分集度直接影响,而编码码率和扩频因子则通过与原始消息序列长度L的约束关系间接影响着通信速率的可变动态范围,约束关系如下

(2)

式中:Rcoding为编码码率;tc为扩频后一个码片持续的时间;Gp为扩频因子;D为最大波形占空比。综合式(1)和式(2)可将通信速率模型表示为

Rb=f1(Qm,C,Rcoding,Gp)

(3)

1.2 被截获概率模型

在射频隐身作战应用中,危及战术数据链通信系统载体安全性的首要问题是敌方无源探测系统对通信射频信号的截获。非合作无源探测系统对通信系统载体安全的威胁可以采用一个特征定量描述,即在给定距离上的被截获概率。

将通信系统射频信号在给定距离d上被敌方非合作无源探测系统截获的概率用PI,d表示。PI,d是空间、时间、频率域三重窗口的重合概率和能量域检测概率的乘积,可表示为

(4)

式中:AF指的是无源探测系统调谐到发射机频率的概率;DI为空间上无源探测系统的密度;T表示无源探测系统的积分时间;TOT为数据链通信系统对无源探测系统的照射时间;PD为无源探测系统探测到发射机波束能量的检测概率。在本文中,假设无源探测系统的前端截获模型是宽带辐射计,无源探测系统位于数据链波束主瓣范围内,则有AFDI=1。因此,被截获概率可简化为

PI,d=min(TOT,T)PD/T

(5)

式中

TOT=LGpCtc/Rcoding

(6)

2个相邻的通信时隙之间需要预留一定的抖动时间,故TOT需满足式(7)所示约束条件

TOT≤Dts

(7)

综合式(6)和式(7),可将TOT表示为

TOT=g1(L,Rcoding,Gp,C,D)

(8)

(9)

式中:PFA表示无源探测系统的虚警概率;γ表示无源探测系统接收端接收到的数据链信号能量与单边带噪声能量的比值,可表示为

(10)

其中,pIr表示单位时间内无源探测系统接收端接收到的数据链信号能量,GTR表示数据链在无源探测系统方向的发射天线增益,GRI表示无源探测系统接收天线增益,LPI表示数据链射频信号在无源探测系统方向的传播损耗,B表示无源探测系统前端滤波器的带宽,N0为噪声功率谱密度,pt表示数据链通信系统发射端的辐射功率。

为保证数据链端机以要求的误码率可靠解调通信信号,则其接收到的通信信号功率应满足通信波形的功率灵敏度要求,即

pr≥pr,min=EbRb+Y0=(Eb/N0)RbN0+Y0

(11)

式中:Eb/N0表示通信速率Rb对应通信波形可靠解调所需的最低每比特信号能量与噪声功率谱密度的比值;Y0表示数据链通信系统的链路余量;pr,min表示通信波形的数据链端机接收功率灵敏度;pr表示数据链端机接收到的通信信号功率,可表示为

pr=ptGTRGRR/LPR

(12)

式中:GTR表示数据链在接收端方向发射天线增益;GRR表示数据链端机接收天线增益;LPR表示数据链射频信号在接收端方向的传播损耗。

综合式(11)和(12)可得,数据链的可靠通信速率与辐射功率存在如下关系

(13)

将式(13)代入式(10),可得

(14)

由式(14)可知,降低γ可通过控制Eb/N0和Rb来实现。Eb/N0是原始消息序列长度、编码码率、扩频因子和调制方式等多个参数的函数,在本文中以实测仿真结果作为先验数据,建立Eb/N0与通信波形参数的映射关系,可以将Eb/N0描述为

Eb/N0=g2(Rcoding,Gp,Qm,L)

(15)

综合式(3)、式(5)、式(8)、式(9)、式(14)和式(15)可得被截获概率模型为

PI,d=f2(g1(L,Rcoding,Gp,C,D),

g2(L,Rcoding,Gp,Qm),f1(Rcoding,Gp,C,Qm))

(16)

1.3 优化模型

在对抗中主动实现射频信号隐蔽,并实现可靠高效的数据传输,是数据链需同时优化的两项目标。数据链的通信波形参数优化问题可以建模为式(17)所示的最优化问题

F(L,Rcoding,Gp,Qm,C)=

(17)

式中:{L}、{Rcoding}、{Gp}、{Qm}、{C}分别为各通信波形参数的取值范围;PI,th为被截获概率门限值,是数据链载体提出的最低安全性要求;Rb,th为通信速率门限值;RI,th为非合作无源探测系统的截获距离门限值;Rd为数据链通信系统的通信距离;Pe,th为系统误码率门限值,是数据链载体提出的最低通信可靠性要求。

式(17)描述的是一个多目标优化问题。根据式(5)和式(14)可知,被截获概率与TOT、Eb/N0都成正比关系。编码码率增大,TOT随之减小,Eb/N0却随之增大。因此,编码的增大能否对被截获概率起贡献作用主要取决于TOT的减小对被截获概率的贡献能否超过Eb/N0的增加对被截获概率的恶化。

同样,由式(1)、式(5)和式(6)可知,波形分集度C增大,一方面能提高数据链的通信速率Rb,但另一方面也会增大数据链的辐射时间TOT,从而导致数据链暴露的风险也随之增大。单独调整某个通信波形参数很难使得2个目标同时达到全局最优解,因此必须建立多目标优化模型对通信波形参数进行联合分析求解。

2 模型求解

本文建立的多目标优化模型有2项优化目标。优化目标f1为数据链通信速率，表征了数据链在单位时间内能可靠有效传输的比特数量。f1量化了数据链系统辐射射频信号对载体的信息保障能力，此目标的优化方向是越大越好。优化目标f2为数据链的被截获概率，它量化了数据链系统辐射射频信号对数据链载体安全性带来的威胁，此目标的优化方向是越小越好。该多目标优化问题可分解为优化方向调整、优化目标归一化和模型转换3个步骤。

2.1 优化方向调整

由于f1、f2优化目标的优化方向不一致，因此首先需调整优化目标f2的优化方向，使其优化方向与f1的优化方向一致。调整f2的优化方向后，即可通过求解总优化目标最大值的方式得到优化解。

2.2 优化目标归一化

优化目标f1和f2的值域相差较大，必须要对2项优化目标进行归一化处理。f1的取值通常远大于1，当数据链通信系统的频谱效率最高时，f2的取值最大，接近于系统的码片速率。f2取值最小时为数据链通信系统的频谱效率最低时。例如，选择调制方式为BPSK，波形分集度为1，通信时隙为5 ms，原始消息序列长度最小值为64，则优化目标f1的最小值为12.8 kb/s。f2的取值通常接近于0，值域为[0～1]。归一化后的优化目标如下式所示

(18)

2.3 模型转换

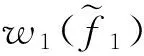
(19)

当满足了载体平台安全性的门限要求后,常量α、β和λ的相对取值大小反映了数据链战术使用策略的偏好,即当使用策略更偏好提高信息共享能力时,则应给β和λ赋予相对更大的值;反之,当使用策略更偏好提高载体平台的安全性时,则应给α赋予相对更大的值。无论常量α、β和λ的相对取值情况如何,常量α、β和λ的值都应远小于∞,这使得载体平台安全性的门限要求具备对式(19)非法解的否决权,从而强迫式(19)的解满足载体平台安全性的门限要求。

3 实验结果分析

非合作无源探测系统参数和数据链系统参数如表1、表2所示。借鉴第三代移动通信系统WCDMA中的Turbo码技术、直接序列扩频技术和BPSK/QPSK/16QAM/64QAM调制技术进行模型验证,通信波形设计技术参数如表3所示。优化模型常量α、β和λ分别为600、300和1/2,信道干扰类型采用宽整脉冲干扰。分别进行3种情况下的计算仿真:①当数据链传输信息载体类型变化时,验证优化模型对通信波形参数的优化能力;②在不同的环境威胁因子下,验证优化模型对环境威胁的应变能力;③在通信性能大致相当的情况下,比较数据链优化前后的射频隐身性能。

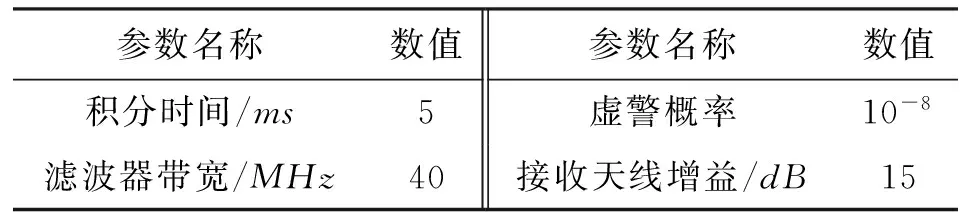
表1 非合作无源探测系统参数

表2 数据链系统参数

表3 通信波形设计技术参数

3.1 仿真1

数据链信息载体类型分为命令和数据2种。命令包括战场态势信息和各种作战指令等信息,具有数据量小、需要快速响应等特点,其安全性需求最高;数据通道则有数据量大、载体信息承载能力要求高等特点,其安全性需求通常较低。参考目前应用最广泛的数据链Link-16的标准数据传输速率范围(28.8～238kb/s)[13],当信息载体类型为命令时,设置通信速率门限Rb,th为25kb/s,截获距离为400km处被截获概率门限值PI,th为10-8;信息载体类型为数据时,设置通信速率门限Rb,th为200kb/s,被截获概率门限值PI,th为10-6。设数据链通信距离RD为150km,非合作无源探测设备的截获距离RI为400km。图1为所有通信波形参数集合的通信速率Rb和被截获概率pI,d对比。

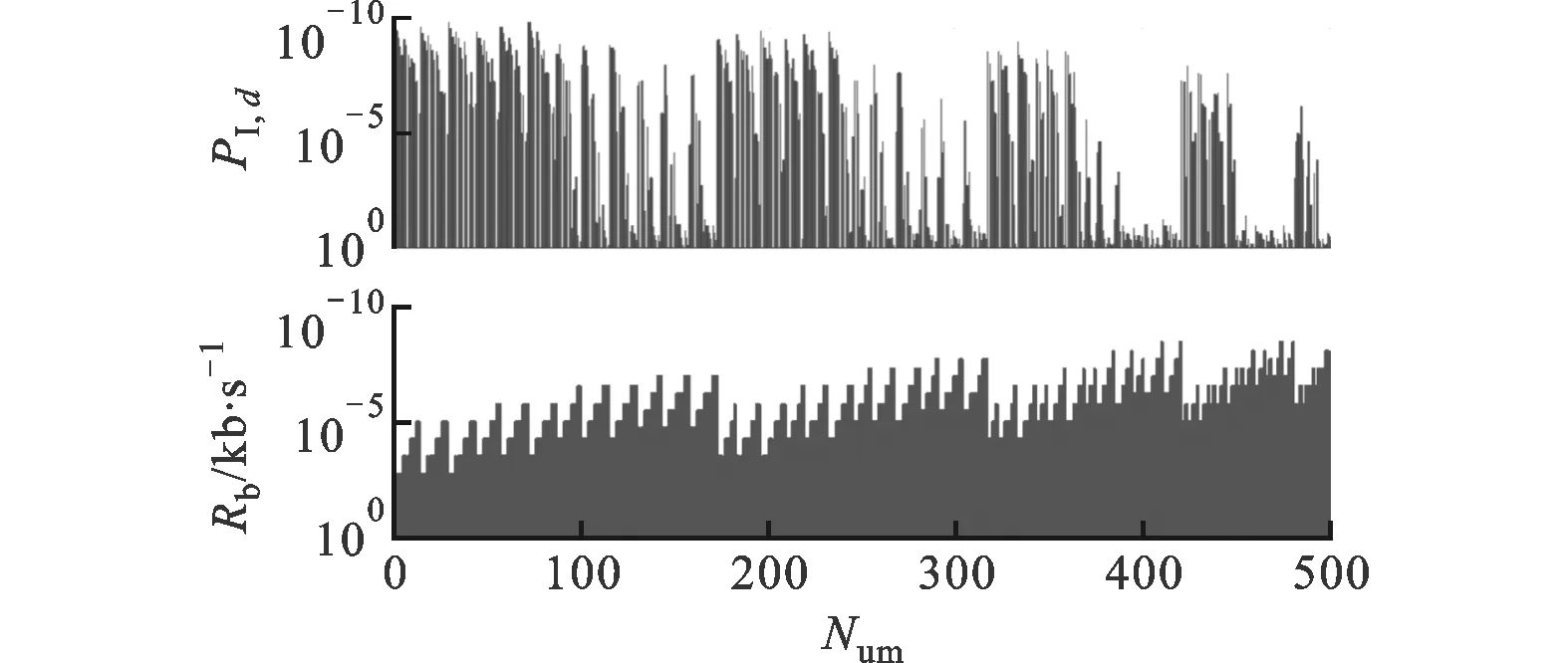
图1 通信波形参数集合的通信速率和被截获概率对比

利用图1中数据进行优化模型的求解,得到2组优化解,其对应的优化目标值和通信波形参数值如表4和表5所示。

表4 优化解对应的优化目标数值

表5 优化解对应的通信波形参数

当数据链传输载体类型为命令时,优化解偏向于保障信息载体的安全,数据链在满足载体信息承载能力条件下,被截获概率仅为6.7×10-9。对应的通信波形参数中,原始消息序列长度较短,满足命令传输快速响应的需求,同时为了有效降低数据链辐射能量,通过信道编码、扩频和调制技术级联作用,所需Eb/N0仅为6.2dB,有利于被截获概率的降低。

当数据链传输载体类型为数据时,优化解偏向于保障载体信息的承载能力。为了达到设定的通信速率门限值,优化模型选择了拥有较长的原始消息序列长度、较高的编码码率和频谱效率较高的调制方式的通信波形参数组合作为优化解,从而使得数据链能较容易满足系统对通信能力的要求,所付出的代价是目标接收机可靠解所需Eb/N0增大至9.0dB,数据链的被截获概率增大至8.6×10-7。与传输载体为命令时相比,传输载体为数据时辐射的通信信号安全性会适度降低。

3.2 仿真2

令α为环境威胁因子,用于表征数据链所处环境的威胁程度,可用下式表示

α=RD/RI

(20)

式中:RD为数据链发射端和目标接收机之间的通信距离;RI为数据链发射端和截获接收机之间的截获距离。在实际作战场景中,由于数据链设备平台的机动特性,RD和RI往往是在不断变化之中的,该信息可通过数据链态势感知得到,可以作为优化模型的先验知识,用于指导优化模型的求解。

α越大,一方面,RD越大,数据链和目标接收机的通信难度相应增大;另一方面,RI越小,数据链越容易被截获接收机截获。因此,α越大,表明数据链所处环境的风险越大;反之,α越小,则风险越小。

令通信速率门限Rb,th为100kb/s,被截获概率门限PI,th为10-7。表6给出了优化模型在4种不同的环境威胁因子下的优化结果。

从表6可知,当环境威胁因子变大,优化模型为满足数据链隐身能力需求,强迫数据链的通信速率降低以实现射频信号的最大化隐蔽。当环境威胁因子最大(α=1.0)时,数据链通信波形在500km处的被截获概率优化解为9.4×10-8,勉强满足通信载体对系统隐身能力所提的要求,所付出的代价是数据链通信系统的通信速率降低为64kb/s,略低于通信载体对系统通信能力所提的要求。

表6 优化模型对不同环境威胁因子的优化结果

3.3 仿真3

本文基于可变的通信波形参数提出了一种射频隐身方法,而优化前的数据链从来都是基于固定的通信波形参数。因此,可以在通信性能大致相当的前提下,比较数据链优化前后射频隐身性能。设数据链通信距离为150 km,截获距离的变化范围为400～800 km,步进为50 km。通信速率和被截获概率门限值分别为100 kb/s和10-7。采用本文提出的优化模型,在不同的截获距离下,得到9组优化解对应的通信速率,如表7所示。

表7 不同截获距离下的优化解对应的通信速率

表7中9组优化解对应的通信速率的平均值为256 kb/s。因此,可选择一组通信速率为256 kb/s的通信波形参数组合作为比较对象。图2为在不同的截获距离下,优化前后数据链的被截获概率对比图。

图2 数据链优化前后被截获概率对比图

由于大气环境对射频信号的衰减作用,随着截获距离的增大,无源探测设备接收端接收到的通信波形信号能量逐渐下降,因此不管是优化前还是优化后,数据链射频信号的被截获概率都会随着截获距离的增大呈现一定程度的降低趋势。由图2可知,截获距离为400～800 km时,本文提出的优化模型所获得的被截获概率比优化前数据链的被截获概率降低9.5～30 dB。在截获距离从800 km减小至400 km的过程中,优化前数据链始终采用固定的通信波形参数进行通信波形信号的辐射,截获接收机接收到的信号功率随截获距离的减小成比例增大,相应地,被截获概率随之快速增大。截获距离为400 km时,数据链面临的被截获概率高达1.58×10-5,低于数据链的安全性要求(1.0×10-7),从而危及数据链载体的安全。与之对比,本文提出的优化模型能更有效地抑制辐射功率从而降低被截获概率,使得截获距离减小时,数据链的被截获概率变化更为平缓。当数据链处于最恶劣环境(截获距离为400 km)时,被截获概率仅为原来的1/1 000,大大提高了数据链的射频隐身性能,有效保障了载体信息的安全。

4 总 结

在作战过程中通过合理配置数据链的通信波形参数可优化数据链的隐身性能。本文在深入分析通信波形参数对数据链射频隐身性能的影响关系的基础上,建立了一种通信波形参数优化模型。本文优化模型对环境威胁有更好的自适应性,在载体信息安全等级提高时,可在约束值范围内适度降低通信速率以减小数据链的被截获概率。与优化前相比,在相同的通信速率条件下优化后数据链的被截获概率大大降低。本文提出的通信波形参数优化模型进一步丰富了射频隐身的理论和方法,对通信波形参数的联合优化有一定的参考价值。

[1]LAURA S.Stealth technology:the potential to make the visible, invisible [C]∥Proceedings of 2014 International Conference on Unmanned Systems.Arlington, VA, USA:Association for Unmanned Vehicle Systems International, 2014:1463-1482.

[2]杨宇晓, 周建江, 陈军, 等.基于最大条件熵的射频隐身数据链猝发通信模型 [J].航空学报, 2014, 35(5):1385-1393.YANG Yuxiao, ZHOU Jianjiang, CHEN Jun, et al.Burst communication datalink model for radio frequency stealth based on conditional maximum entropy [J].Acta Aeronautica et Astronautica Sinica, 2014, 35(5):1385-1393.

[3]杨宇晓, 周建江, 陈卫东, 等.基于空间信息的射频隐身数据链最优能量控制算法 [J].宇航学报, 2013, 34(7):1008-1013.YANG Yuxiao, ZHOU Jianjiang, CHEN Weidong, et al.An optimal energy control algorithm for radio frequency stealth datalink based on spatial information [J].Journal of Astronautics, 2013, 34(7):1008-1013.

[4]BARK G.Power control in an LPI adaptive frequency-hopping system for HF communications [C]∥Proceedings of 1997 International Conference on High Frequency Radio Systems and Techniques.Piscataway, NJ, USA:IEEE, 1997:301-305.

[5]YANG H B, ZHOU J J, WANG F, et al.Design and analysis of Costas/PSK RF stealth signal waveform [C]∥Proceedings of 2011 International Conference on Radar.Piscataway, NJ, USA:IEEE, 2011:1247-1250.

[6]DILLARD G M, REUTER M, ZEIDLER J, et al.Cyclic code shift keying:a low probability of intercept communication technique [J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3):786-798.

[7]REED D E, WICKERT M A.Spread spectrum signals with low probability of chip rate detection [J].IEEE Journal on Selected Areas in Communications, 1989, 7(4):595-601.

[8]WANG Y H, PAPADOPOULOS H C.Physical-layer secrecy in AWGN via a class of chaotic DSSS systems:analysis and design [J].IEEE Transactions on Signal Processing, 2004, 52(9):2637-2649.

[9]LI Y S, WU C, SUN D Y, et al.A new physical layer transmission scheme for LPI and high throughput in the cooperative SC-FDMA system [J].Journal of Communications and Networks, 2013, 15(5):457-463.

[10]FANCEY C, ALABASTER C M.The metrication of low probability of intercept waveform [C]∥Proceedings of 2010 International Conference on Waveform Diversity and Design.Piscataway, NJ, USA:IEEE, 2010:58-62.

[11]LIU R H, LUO J H, SPASOJEVIC P.Adaptive transmission with variable-rate turbo bit-interleaved coded modulation [J].IEEE Transactions on Wireless Communications, 2007, 6(1):3926-2936.

[12]梅文华, 蔡善法.JTIDS/Link16数据链 [M].长沙:国防工业出版社, 2007:19-20.

(编辑 刘杨)

An Optimization Model for Communication Waveform Parameters of Radio Frequency Stealth Datalink

XIE Guihui1,TIAN Mao1,WANG Zhenghai2,TANG Xiaoqing1,LI Jie1

(1.School of Electronic Information, Wuhan University, Wuhan 430072, China; 2.Southwest China Institute of Electronic Technology, Chengdu 610036, China)

An optimization model for communication waveform parameters based on radio frequency (RF) stealth is proposed to solve the problem of high intercept probability of datalinks in adverse environment.According to the prior knowledge of the communication distance and intercept distance obtained from environmental awareness system, the original message sequence length, channel coding rate, spreading factor, modulation mode and signal diversity are regarded as optimization parameters of the model, and the communication rate and intercept probability at given distance are taken as optimization objectives.The gross optimization objective of the model is generated from these two objectives through normalization and linear weighting.The traversing method is used to find the maximal value of the gross objective, and the corresponding communication parameters are taken as the optimal solution.Simulation results show that when the security level of the carrier information increases, the model decreases the communication rate moderately within the constraint value range, and the intercept probability is decreased from 8.6×10-7to 6.9×10-9.It is also shown that under the same communication rate level, the intercept probability of the model’s datalink is 1/1 000 of that before optimization in the most adverse environment.Thus, the RF stealth performance improves significantly.

datalink; radio frequency stealth; communication waveform parameters; optimization model

2014-06-23。 作者简介:谢桂辉(1988—),男,博士生;田茂(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61261010)。

时间:2015-01-16

http:∥www.cnki.net/kcms/detail/61.1069.T.20140116.1510.004.html

10.7652/xjtuxb201504019

TN975

A

0253-987X(2015)04-0116-07