联合时延与多普勒频率的直接定位改进算法

王云龙,吴瑛

(解放军信息工程大学信息系统工程学院,450000,郑州)



联合时延与多普勒频率的直接定位改进算法

王云龙,吴瑛

(解放军信息工程大学信息系统工程学院,450000,郑州)

针对传统两步定位算法中测量参数不能保证与真实位置匹配,导致信息损失,产生定位误差的问题,提出了一种联合时延与多普勒频率的直接定位改进(IDPD)算法。首先采用高斯最大似然估计器,将从数据中提取目标位置信息的问题转化为求解包含发射源位置信息的厄尔米特矩阵的最大特征值问题;然后利用矩阵转置后特征值相同这一性质进行简化运算;最后通过二维地理网格搜索以获取发射源的位置估计。较之传统的直接定位(DPD)算法,IDPD算法对信号无要求,且利用极大特征值作为网格点的代价函数,抑制了噪声的影响,提高了定位精度。仿真结果表明,IDPD算法在低信噪比条件下对目标位置估计误差在102m量级,与DPD算法相比,定位精度提高了30%以上,更加逼近克拉美罗下界。

直接定位;最大似然;无源定位;特征值分解;克拉美罗下界

传统的无源定位体制一般均采用两步定位法,即首先进行参数估计,如到达角度(angle of arrival,AOA)[1]、到达时间(time of arrival,TOA)[2]、到达时间差(time difference of arrival,TDOA)[3]、多普勒频差(differential of doppler,DD)[4]、接收信号强度(received signal strength,RSS)[5]及多种参数联合估计[6-9]等,再通对获取的参数进行位置解算获得目标的位置估计。由于传统的两步定位法需要首先获得目标的相关参数,然后通过解定位方程来得到目标的位置估计,这就使得参数估计和位置解算相分离,无法保证测量的参数与真实目标的位置信息相匹配,导致数据处理过程中不可避免地存在信息损失,从而无法获得最优的估计性能。因此,如何能够从数据中直接获取目标的位置信息就成为当前的研究热点[10-15]。

Dornon等人首先分析了确定性最大似然估计器(deterministic ML,DM)和高斯最大似然估计器(Gaussian ML,GM)用于宽带发射源定位时的性能[10]。Weiss等人通过构造最大似然代价函数,在定义的地理网格中进行二维搜索直接得到目标的位置估计,提出了与两步定位法相区别的一种新的定位方法——直接定位法(direct position determination,DPD)[11-13],能够在低信噪比条件下逼近克拉美罗下界(Cramér-Rao lower bound,CRLB)。DPD算法将参数估计与位置解算融合到一个模型当中,避免了传统定位方法中因两步分离而造成的信息损失;同时,DPD算法中融合了所有观测站的数据信息,避免了多目标定位中“数据-发射源关联”的问题[14]。

文献[12]中构造的代价函数的方式受到信号形式的限制,且其2-范数加和的方式未能充分利用各观测站信息。对此,本文提出了一种联合时延与多普勒频率的直接定位改进(improved DPD,IDPD)算法,将转化到频域的数据构造高斯最大似然估计器,并对包含发射源位置信息的厄尔米特矩阵特征值分解,将位置估计问题转化为求解最大特征值的问题,最后通过地理网格匹配搜索得到目标位置的估计。本文算法能够充分利用各观测站的信息,进一步提高了定位的精度并逼近CRLB。另外,文献[12]中未分析多目标及观测站位置存在误差条件下算法的定位性能,针对上述问题,本文分别对观测站数量以及误差对IDPD算法的影响进行了分析讨论,并与传统的算法进行了对比,最后通过仿真验证了本文算法的有效性。

1 问题模型

假设存在一个目标发射源,发射带宽为W、载频为fc的信号s(t),位置坐标为p0;L个移动的观测站在K个观测间隙内对发射源的数据进行截获,用pl,k和vl,k(l=1,…,L;k=1,…,K)表示第l个观测站在第k个观测间隙内的位置与速度,则相应观测站在t时刻接收到的数据模型为[12]

rl,k(t)=bl,ksk(t-τl,k)ej2πfl,kt+nl,k(t)

0≤t≤T

(1)

式中:bl,k为信道传播衰减参数;T为观测间隙内的观测时间;nl,k(t)为0均值、广义平稳的复高斯白噪声;τl,k为信号到达第l个观测站第k个观测间隙时的时延;fl,k为观测站与目标相对位移引起的多普勒频移

τl,k=‖p0-pl,k‖2/c

(2)

(3)

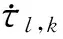
将接收数据rl,k(t)用傅里叶系数表示,则式(1)可以写为[12]

(4)

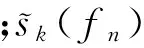
若将式(4)用向量表示,可得

(5)

式中

(6)

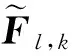
(7)

2 联合时延与多普勒频率的直接定位改进算法

文献[12]中给出的代价函数为

(8)

式中:Γ为对角阵为接收数据的代价函数;σ2为噪声功率。

这样,对目标位置的估计可以转化为求式(8)代价函数的最大似然估计,即

(9)

构造如下最大似然函数

(10)

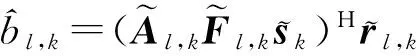
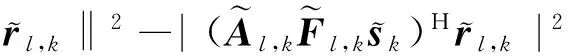
(11)

(12)

式中:Qk。通过对比式(12)与式(8),若忽略式(8)代价函中噪声(即σ2Λ-1)的影响,本文中的式(12)与式(8)具有类似的形式,只是不再需要这一近似要求,而且还能够利用信号的信息。但是,实际应用中一般无法获知信号的先验信息,此时式(12)的最大化可认为是对关于二次型的最大化。因此,应选择与矩阵Qk最大特征值相一致的特征向量。

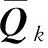
(13)

最后,通过设定搜索的网格范围,并求式(13)得最大值,其对应的坐标即为发射源的位置

(14)

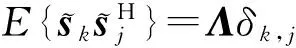
3 误差与运算量分析

3.1 误差分析

直接定位算法由于不需要进行参数估计,因此可避免参数误差导致的定位误差。但是,实际观测过程中,观测站的位置可能无法准确获知,导致按照理想模型对目标位置进行估计就会不准确。

考虑误差时,将式(1)修正为带误差的数据模型

0≤t≤T

(15)

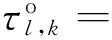
(16)

fl,k

(17)

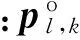
定义观测站误差向量Δpl,k为观测站位置真实值与测量值之差

Δp=po-p

(18)

假设Δp为零均值高斯分布,则其协方差可表示为

E[ΔpΔpT]=Qp

(19)

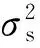
(20)

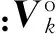
3.2 运算量分析

4 仿真实验

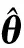
(21)

式中:I(θ)表示费希尔信息矩阵(Fisher information matrix,FIM)。本文中,FIM为包含目标位置的二维坐标参数的矩阵,其中的元素表示为[12]

(22)

式中

(23)

其中GIL-1L,L/L;Ф=WTRSN/(12π),RSN为信噪比。

4.1 单发射源

首先,定义均方根误差为

(24)

仿真条件参考文献[12]的设置:假设存在一个静态发射源,位置坐标为(2 500 m,2 500 m),发射信号是载频fc=1 GHz,带宽为300 kHz的高斯信号,其传播速度c=3×108m/s;选取每个观测间隙时间为T=0.972 ms≫Δτl,k,两观测站的观测间隔为3.33 s≫T;存在位置分布考虑如图1所示的观测站,移动速度为300 m/s。各观测站的地理位置信息如表1所示。

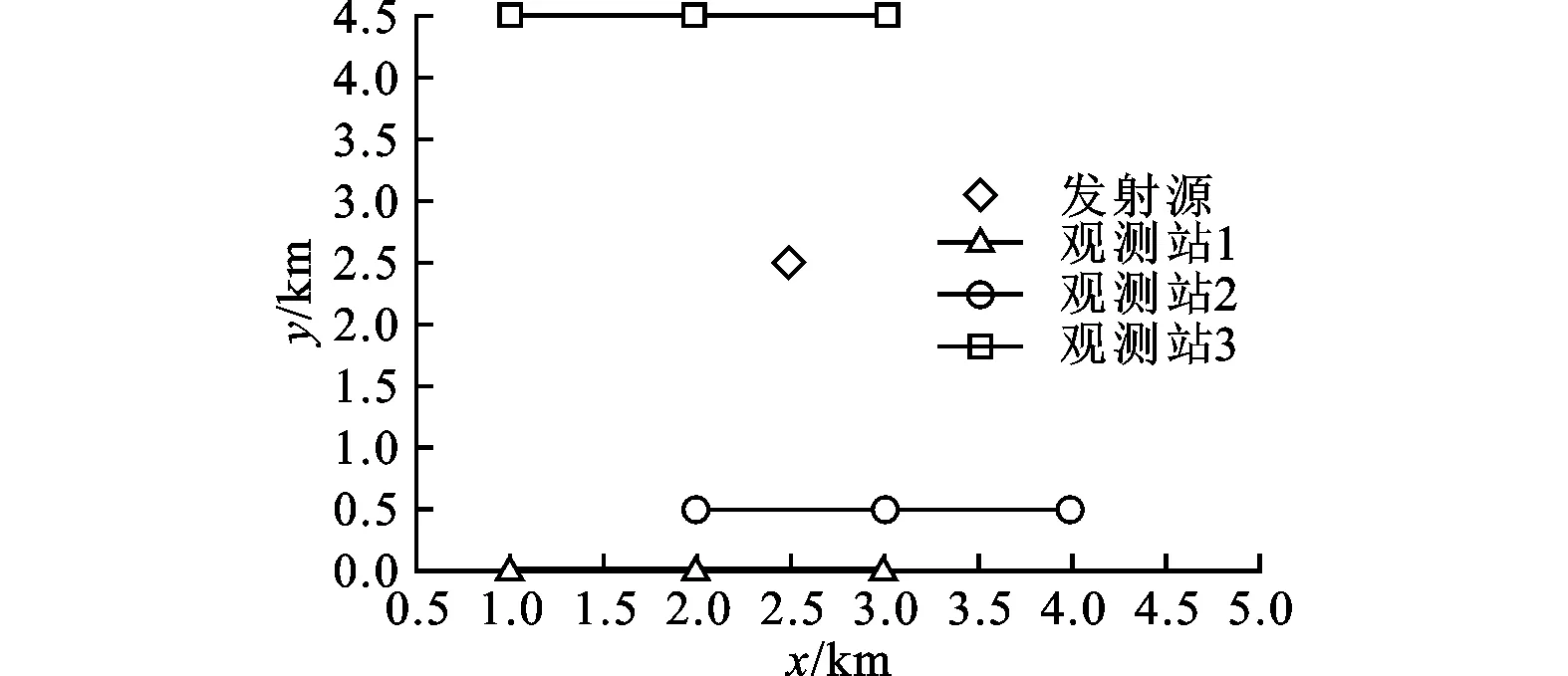
图1 目标发射源与观测站间的地理位置关系

采用文献[12]的直接定位算法(原始DPD算法)、文献[6]的Taylor级数迭代两步定位算法(两步定位算法)以及本文IDPD算法进行仿真对比。图2给出了不同算法随信噪比变化时的均方根误差曲线,从中可以看出:DPD算法在低信噪比时其误差数量级在10-2,而两步定位法的误差数量级在10-3,即DPD算法的性能优于传统的两步定位法;另外,本文算法的性能也优于原始的DPD算法,且更靠近CRLB。

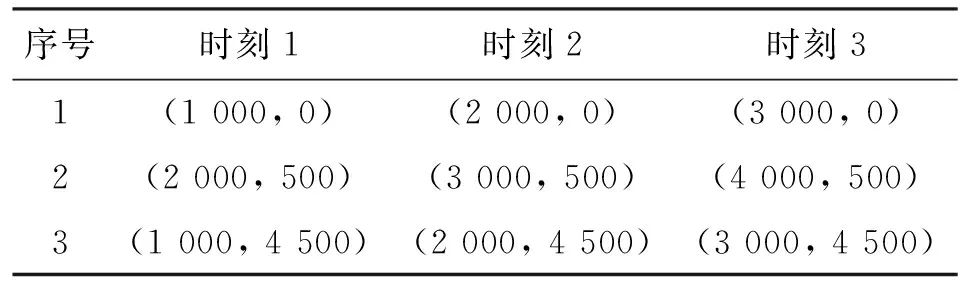
表1 各观测站地理位置 m

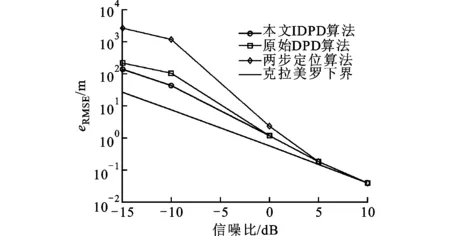
图2 不同算的估计法性能对比

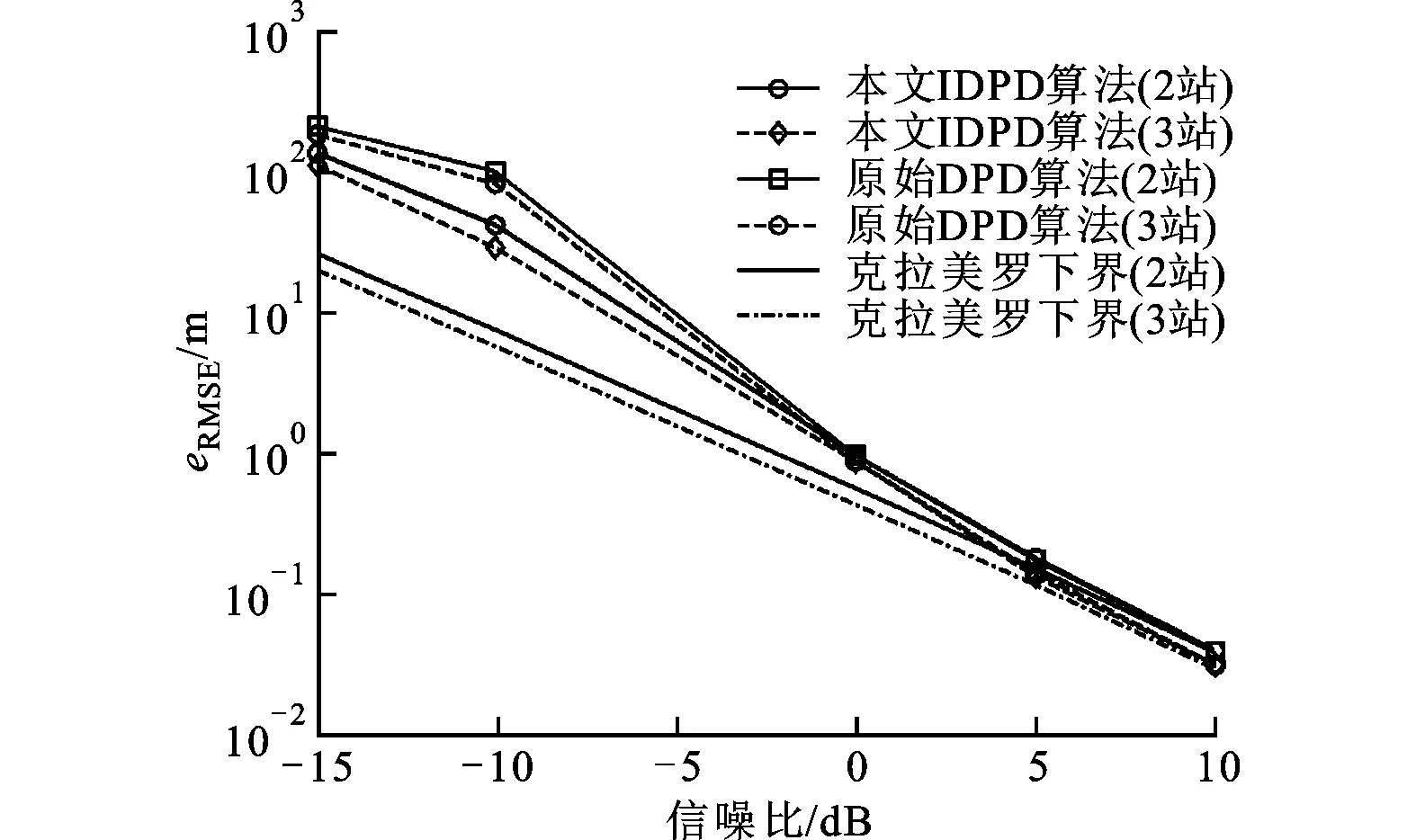
图3 观测站数量对估计性能的影响

图3给出了增加一个观测站3后本文算法与原始DPD算法的估计性能对比。从图中可以看出,2种算法在对单发射源定位的情况下,增加观测站均能进一步提高定位的精度。图4显示了当观测站存在误差时对不同算法定位性能的影响,可以看出,DPD算法对误差的敏感程度远小于两步定位法。这是因为在两步定位过程中,位置误差经过参数估计可能被放大,再经过位置解算进一步引入误差,最终导致的估计偏差较大,因此对于位置的误差也相对比较敏感。

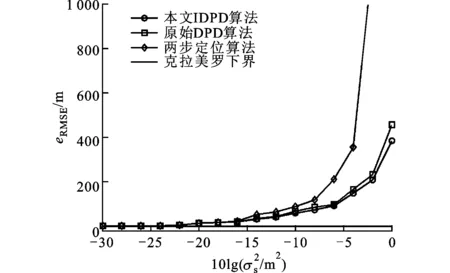
图4 观测站位置误差对估计性能的影响

4.2 多发射源

文献[14]中指出DPD算法融合了所有的观测信息,解决了“数据-发射源关联”的问题,即相对于传统的两步定位法还需要对目标和数据进行匹配,而直接定位法仅通过增加额外维度的发射源信息并通过网格搜索就能得到多个发射源的位置估计。文献[12]中讨论DPD算法的性能时仅对单目标进行讨论,而没有讨论对于多发射源存在时算法的分辨性能。下面将对这一问题进行分析。

设置发射源位置间隔由远至近,并分析算法对发射源位置的估计性能,仿真选择信噪比为5 dB,其余仿真条件同4.1。图5和图6分别显示了利用2个观测站和3个观测站对2个发射源定位时的等高线图;表2和表3给出了2个发射源间隔变化时算法对发射源位置的估计误差。

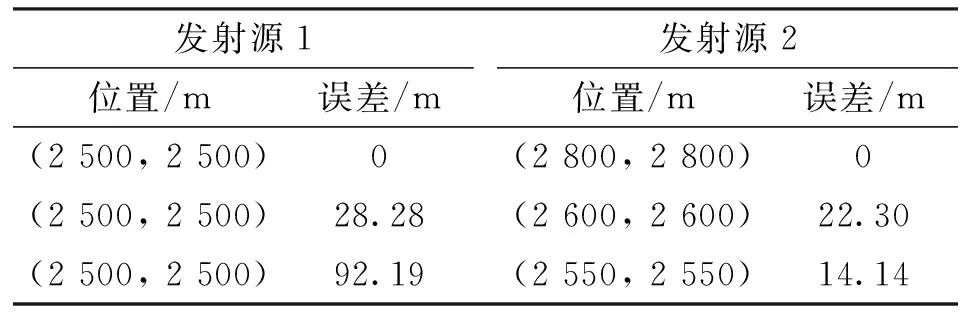
表2 2站对2个发射源的定位误差

考虑发射源间的位置关系:①发射源相对较远时,观测站对目标的位置估计结果如图5a、图6a所示,算法能够区分出2个发射源的位置;②发射源相对较近时,观测站对目标的位置估计结果如图5b、图6b所示,由于对目标进行定位时,观测站对于2个发射源定位的交汇谱互相重合,因此叠加在一起的谱线造成了真实峰值的模糊并出现了大量的伪峰。

表3 3站对2个发射源的定位误差

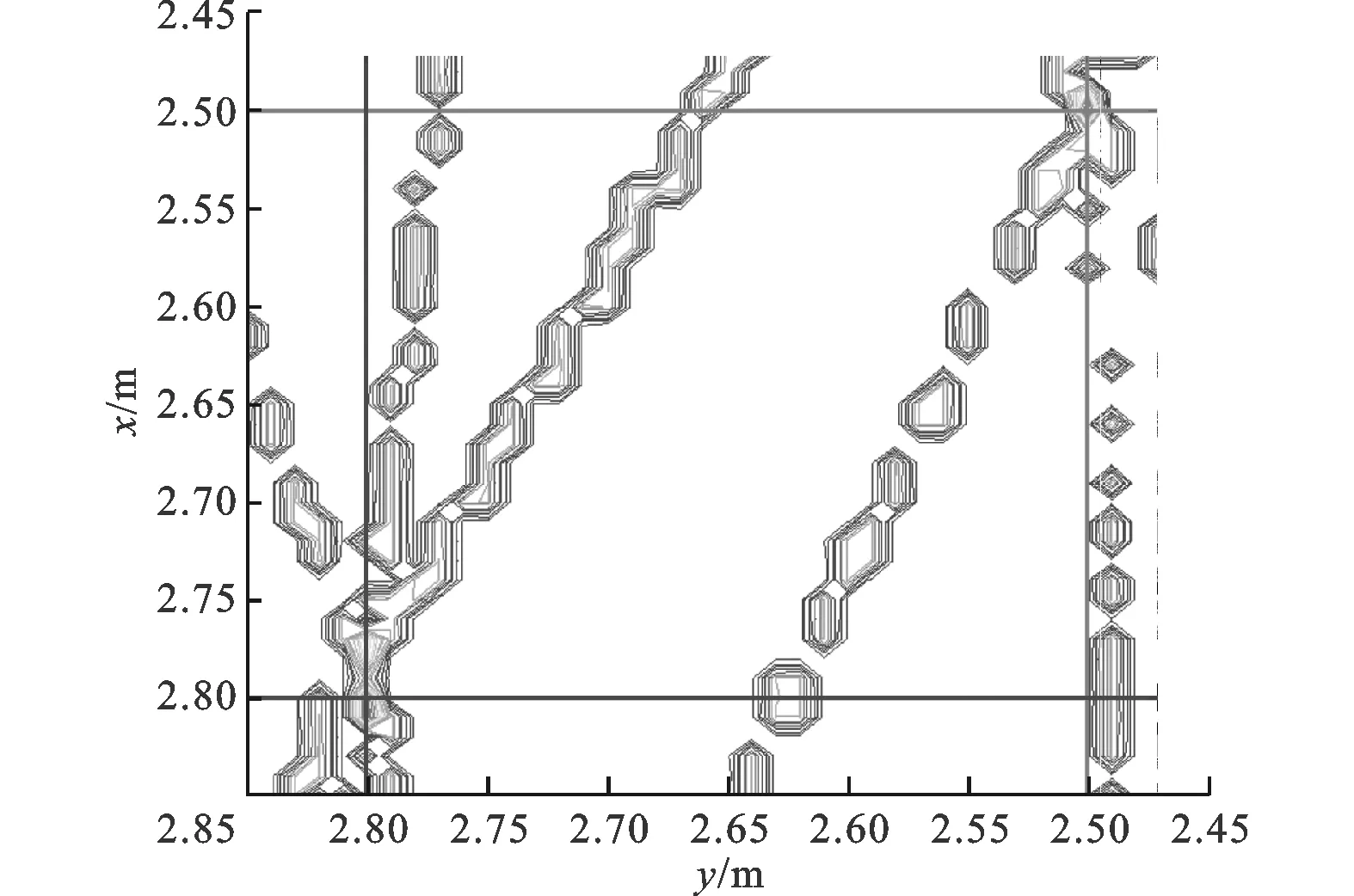
(a)发射源相对较远时的定位等高线图(2站)

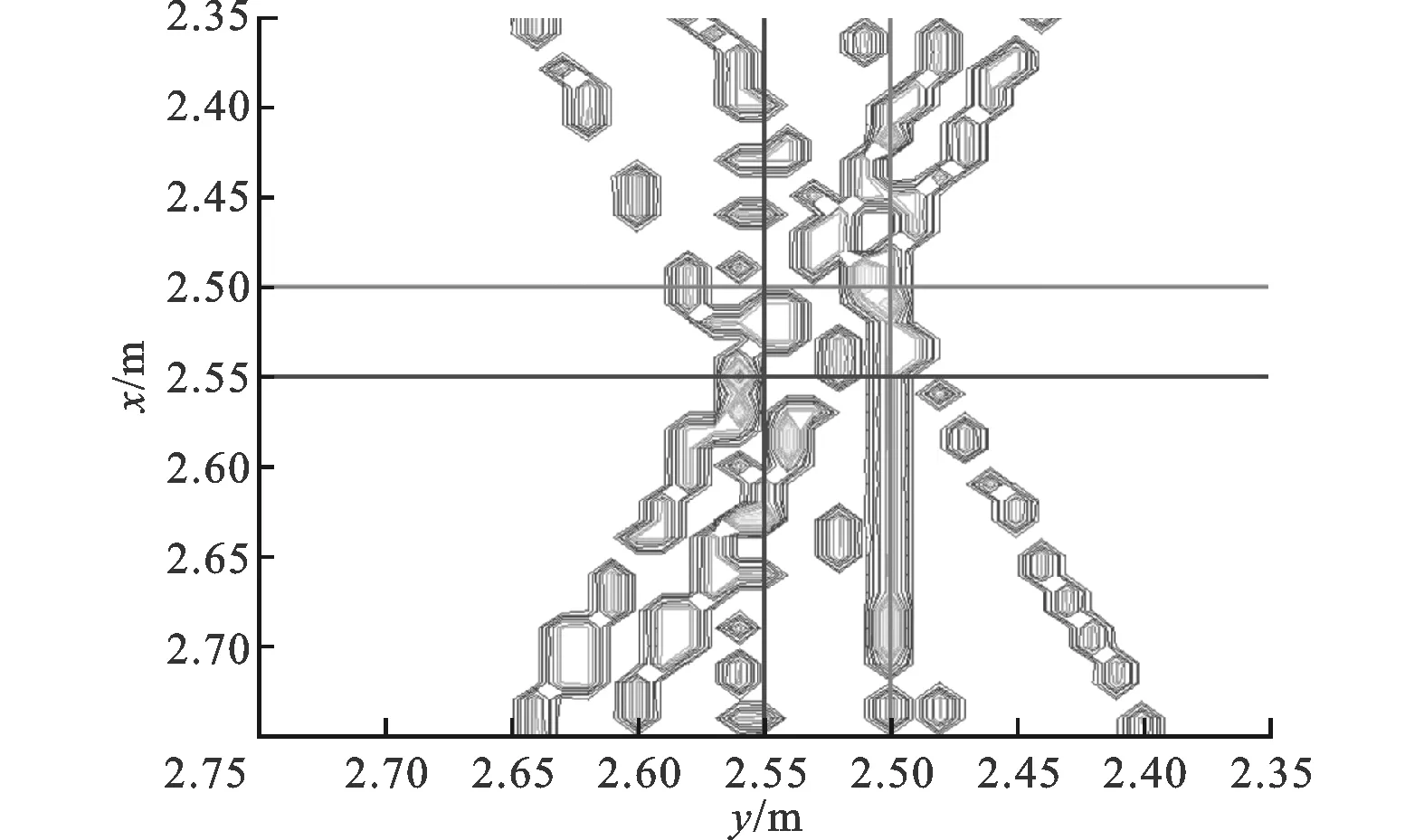
(b)发射源相对较近时的定位等高线图(2站)图5 2站对2个发射源的分辨效果图

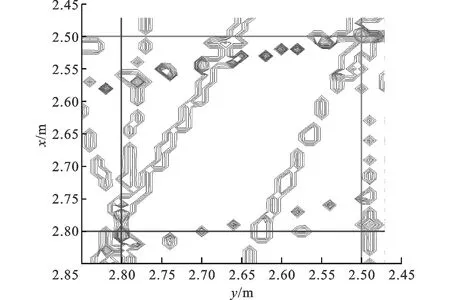
(a)发射源相对较远时的定位等高线图(3站)

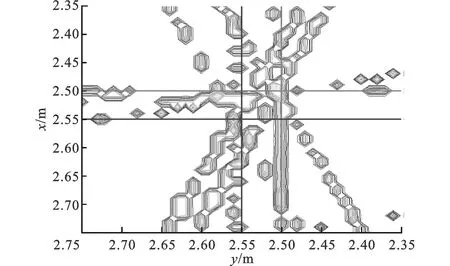
(b)发射源相对较近时的定位等高线图(3站)图6 3站对2个发射源的分辨效果图

对比图5和图6可以看出:对于近距离的发射源,增加观测站会进一步增加定位谱的交汇,导致伪峰增多,使得定位性能下降。对比表2和表3也可以看出:当2个发射源位置较为接近时,算法往往只能对其中一个具有较好的估计,另外一个目标则可能受到伪峰的影响而估偏,所以增加观测站对间距较近的发射源反而会增大定位误差,这是因为更多的交汇轨迹会造成大量的伪峰出现,致使估计不准确。当2个发射源位置较远时,增加观测站能够加强发射源真实位置的谱峰,而对伪峰的影响相对较弱,此时能够提高估计的性能。

5 结束语

本文给出了一种利用时延与多普勒频率信息的直接定位改进算法,将含有目标位置信息的数据构造成信息矩阵,将问题转化为求信息矩阵的最大特征值,进一步提高了算法的定位精度。仿真给出了单发射源条件下与其他算法的性能对比,以及多发射源条件下算法的性能分析,与传统的两步定位法相比,本文的IDPD算法无需参数估计,算法简单易于实现,且在低信噪比条件下的估计精度较高。

[1]XU Jun, MA Maode, LAW C L.AOA cooperative position localization [C]∥IEEE Global Telecommunications Conference on Signal Processing.Piscataway, NJ, USA:IEEE, 2008:1-5.

[2]OH D, KIM S, YOON S H, et al.Two-dimensional ESPRIT-like shift-invariant TOA estimation algorithm using multi-band chirp signals robust to carrier frequency offset [J].IEEE Transactions on Wireless Communications, 2013, 12(7):3130-3139.

[3]GARDNER W A, CHEN C K.Signal-selective time-difference-of-arrival estimation for passive location of man-made signal sources in highly corruptive environments:part I Theory and method [J].IEEE Transactions on Signal Processing, 1992, 40(5):1168-1184.

[4]杨洁, 刘聪锋.迭代频差定位算法及其性能分析 [J].西安电子科技大学学报, 2014, 40(5):8-14.YANG Jie, LIU Congfeng.Iteration FDOA location algorithm and its performance analysis [J].Journal of Xidian University, 2014, 40(5):8-14.

[5]KOWEERAWONG C, WIPUSITWARAKUN K, KAEMARUNGSI K.Indoor localization improvement via adaptive RSS fingerprinting database [C]∥2013 International Conference on Information Networking.Piscataway, NJ, USA:IEEE, 2013:412-416.

[6]HO K C, CHAN Y T.Geolocation of a known altitude object from TDOA and FDOA measurements [J].IEEE Transactions on Aerospace Electron System, 1997, 33(3):770-783.

[7]曲付勇, 孟祥伟.基于约束总体最小二乘方法的到达时间差到达频差无源定位算法 [J].电子与信息学报, 2014, 36(5):1075-1080.QU Fuyong, MENG Xiangwei.Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm [J].Journal of Electronic and Information Technology, 2014, 36(5):1075-1080.

[8]YEREDOR A, ANGEL E.Joint TDOA and FDOA estimation:a conditional bound and its use for optimally weighted localization [J].IEEE Transactions on Signal Processing, 2011, 59(4):1612-1623.

[9]束峰, 朱伟强, 陆锦辉, 等.基于最大比合并的最大似然TDOA/FDOA联合定位算法 [J].宇航学报, 2010, 31(4):1143-1148.SHU Feng, ZHU Weiqiang, LU Jinhui, et al.Maximum ration combing based maximum likelihood TDOA/FDOA joint localization [J].Journal of Astronautics, 2010, 31 (4):1143-1148.

[10]DORON M A, WEISS A J.Maximum likelihood localization of wideband sources [C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing.Piscataway, NJ, USA:IEEE, 1992:23-26.

[11]WEISS A J.Direct position determination of OFDM signals [J].IEEE Transactions on Signal Processing Letters, 2007, 44(6):225-230.

[12]WEISS A J.Direct geolocation of wideband emitter based on delay and Doppler [J].IEEE Transactions on Signal Processing, 2011, 59(6):2513-2521.

[13]AMAR A, WEISS A J.Localization of radio emitters based on Doppler frequency shifts [J].IEEE Transactions on Signal Processing, 2008, 56(11):5500-5508.

[14]HUANG Ling, LU Yilong.Performance analysis of direct position determination for emitter source positioning [J].American Journal of Signal Processing, 2012, 2(3):41-45.

[15]AMAR ALON, WEISS A J.Direct position determination in the presence of model errors-known waveforms [J].Elsevier Digital Signal Processing, 2006, 16:52-83.

[16]KAY S M.Fundamentals of statistical signal processing:estimation and detection theory [M].Beijing, China:Publishing House of Electronics Industry, 2012.

[本刊相关文献链接]

李彬,王文杰,殷勤业,等.一种利用天线旋转的无线传感器网络定位算法.2011,45(4):60-66.[doi:10.7652/xjtuxb 201104011]

王文杰,张渭乐,殷勤业.利用离去角度的无线传感器网络分布式节点定位方法.2010,44(2):61-66.[doi:10.7652/xjtuxb201002013]

魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法.2014,48(6):1-6.[doi:10.7652/xjtuxb 2014 06001]

屈鉴铭,刘志镜,贺文骅.结合有向场景运动模式的粒子滤波行人跟踪方法.2014,48(12):74-79.[doi:10.7652/xjtuxb 201412012]

吴仁斌,姚敏立,贾维敏,等.采用幅度响应约束的鲁棒自适应波束形成算法.2014,48(4):109-114.[doi:10.7652/xjtuxb201404019]

赵梦琰,李扩,鲍刚,等.利用小波包的脑电源定位算法仿真研究.2013,47(12):130-136.[doi:10.7652/xjtuxb2013 12022]

司栋森,李增智,王晓旭.采用四象限探测器的智能跟踪定位算法.2012,46(4):13-17.[doi:10.7652/xjtuxb201204003]

刘学,焦淑红.拟蒙特卡罗自适应粒子滤波的机载无源定位算法[J].西安交通大学学报,2011,45(9):34-39.[doi:10.7652/xjtuxb201109007]

朱磊,水鹏朗,章为川,等.利用区域划分的合成孔径雷达图像相干斑抑制算法.2012,46(10):83-88.[doi:10.7652/xjtuxb201210015]

李彬,王文杰,殷勤业,等.无线传感器网络节点协作的节能路由传输.2012,46(6):1-6.[doi:10.7652/xjtuxb201206001]

(编辑 刘杨)

An Improved Direct Position Determination Algorithm with Combined Time Delay and Doppler

WANG Yunlong,WU Ying

(Institute of Information System Engineering, Information Engineering University of PLA, Zhengzhou 450000, China)

An improved direction position determination (IDPD) algorithm with combined time delay and Doppler is proposed to solve the problem of positioning errors due to the information loss from the mismatch between measured parameters and actual location in traditional two steps localization algorithm.A Gaussian maximum likelihood estimator is employed to transform the problem of extracting target position information into the problem of calculating the maximum eigenvalue of a Hermite matrix which contains the emitter’s location information.Then, the property of eigenvalue keeping unchanged after matrix transpose is used to simplify the calculation.The emitter’s position is finally estimated through the search of two-dimensional geo-grid.Compared with the traditional direct position determination (DPD) algorithm, the IDPD does not need any special requirements for signals and restrains the effect of noise by taking the maximum eigenvalue as the cost function, therefore the position accuracy can be improved.Simulation results show that the performance of the proposed algorithm reaches a 102meter magnitude even under low signal to noise ratio.Comparison with the DPD shows that the positioning accuracy of the IDPD increases by 30% and is closer to the Cramér-Rao lower bound.

direct position determination; maximum likelihood; passive location; eigenvalue decomposition; Cramér-Rao lower bound

2014-09-05。 作者简介:王云龙(1990—),男,硕士生;吴瑛(通信作者),女,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61201381);信息工程学院未来发展基金资助项目(YP12JJ202057)。

时间:2015-01-16

http:∥www.cnki.net/kcms/detail/61.1069.T.20150116.1510.002.html

10.7652/xjtuxb201504020

TN911.7

A

0253-987X(2015)04-0123-07