基于二元液滴碰撞模型的喷雾计算研究

张 璜，薄涵亮，张 帆

（清华大学 核能与新能源技术研究院，北京 100084）

喷雾装置广泛存在于核能设备中。稳压器顶部设置喷雾管，当内部压力偏高时，通过喷雾降低系统压力；压水堆安全壳中采用喷淋装置，通过喷淋出的喷雾降低严重事故下安全壳内的温度和去除泄漏的含放射性的气态碘［1-3］。因此喷雾装置的设计关系到核电站运行的安全性。

喷雾中含有大量液滴，它们在运动过程中相互碰撞，导致喷雾内液滴数目、大小和速度等参数的改变，从而影响喷雾的形态。而喷雾的形态是设计喷雾装置的关键参数。因此通过数值模拟方法建立并求解液滴运动碰撞模型，从而定量模拟喷雾的形态，会为喷雾装置的设计提供依据。

喷雾中大量液滴在运动的同时发生碰撞。由于液滴碰撞过程的复杂性，一般在模型中仅考虑两个液滴同时发生碰撞（二元液滴碰撞）。二元液滴碰撞模型由O'Rourke于1981年 首 次 提 出［4］，并 在KIVA 和FLUENT 等 商用软件中得到广泛使用。O'Rourke模型仅考虑二元液滴碰撞后发生聚合和分离两种机制，对聚合或分离后液滴的速度和大小进行模化。然而Qian和Law［5］在实验中观察到二元液滴碰撞会发生反弹、聚合、拉伸分离和反溅分离等机制。他们的实验结果也被后来的学者证实［3］。然而目前尚无较为完整的判别准则对以上几种碰撞机制进行描述，而且对于碰撞后液滴的速度和大小也无相应的模型进行刻画。

基于以上不足，本文提出二元液滴碰撞的新型模型。该模型综合Rabe等［3］和Post等［6］的研究成果，完整地考虑二元液滴碰撞的反弹、聚合、拉伸分离和反溅分离等机制，对每种机制建立判别准则。同时根据质量和动量守恒关系，综 合Munnannur等［7］、Kim 等［8］和Ko等［9-10］关于碰撞后液滴的研究结果，建立相应的模型计算碰撞后新生成液滴的数目、大小和速度。

1 碰撞机制

二元液滴碰撞存在反弹、聚合、拉伸分离和反溅分离等机制。常用以下3 个无量纲数来表述。

直径比Δ：定义为Δ＝ds／dl，其中ds和dl为小液滴和大液滴的直径。

韦伯数We：定义为We＝ρddsu2／σ，表示惯性力与表面张力的比值，其中ρd 为液滴密度，u为液滴间相对速率，σ为液滴表面张力系数。

碰撞参数I：定义为I＝2b／（ds＋dl），其中b表示两液滴接触时的几何关系（图1）。

图1 碰撞参数bFig.1 Collision parameter b

Qian和Law 通过实验确定了二元液滴碰撞的所有机制，并将其总结成为We-I 相图［5］（图2）。由图2可知，二元液滴碰撞共有5 种机制，即聚合（Ⅰ）、反弹（Ⅱ）、聚合（Ⅲ）、反溅分离（Ⅳ）和拉伸分离（Ⅴ）。其中，机制Ⅰ和机制Ⅲ虽都为聚合，但它们发生的条件不同。

图2 二元液滴碰撞机制Fig.2 Binary-droplet collision regime

1）考虑聚合（Ⅰ）的判别准则

当液滴相对运动的速度非常低时，液滴间的气体压强与环境压强相同，无法对两液滴的相对运动起阻碍作用，此时两液滴直接聚合。Post等［6］认为聚合（Ⅰ）和反弹（Ⅱ）的分界线为直线，并假设We 和I 满足如下关系时发生聚合：

2）考虑反弹（Ⅱ）的判别准则

两液滴相对运动，当液滴快速靠近时，导致液滴间气体压强变大，这些气体形成气膜阻止液滴继续前进。当相对速度减为0时两液滴还未发生接触，则它们反弹开来。Post等［6］考虑液滴间气体密度变化对反弹结果的影响，提出判断反弹机制的判别关系式为：

式（2）中Ф′为形变参数，它表征液滴间气膜密度对反弹作用的影响，可由下式确定：

其中，ρg 为液滴周围环境气体的密度。

3）考虑聚合（Ⅲ）、反溅分离（Ⅳ）和拉伸分离（Ⅴ）的判别准则

当两液滴相对速度较大时，中间气膜无法阻止它们直接接触。在接触后，由于液滴内部流体黏性耗散和液滴表面张力的共同作用使液滴速度减小，以致液滴无足够动能使两者分开，从而两液滴发生聚合。

如果液滴间相对速度足够大，以至于两液滴碰撞接触后，即使由于液滴内部流体黏性耗散和表面张力的作用也无法维持两液滴的聚合状态，则两液滴发生分离。根据两液滴碰撞时的相对位置，将分离分为拉伸分离和反溅分离两类。

Rabe等［3］为简化聚合（Ⅲ）、拉伸分离（Ⅳ）和反溅分离（Ⅴ）的判别准则，将We 和Δ 转换为对称韦伯数Wes，其定义式为：

聚合只发生在Wes＜2.5 时，此时发生聚合的判据为：

发生反溅分离的判别式为：

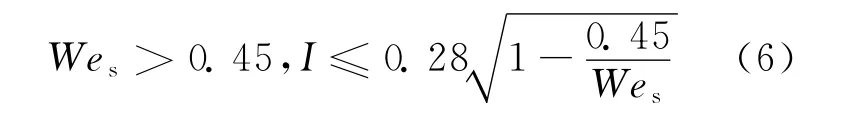
发生拉伸分离的判别式为：

当Wes≥2.5时，二元液滴碰撞后不再发生聚合，只发生反溅分离和拉伸分离。在这种情况下，当I＞0.253时，发生拉伸分离；反之，发生反溅分离。

2 碰撞后液滴

如前文所述，二元液滴碰撞会出现反弹、聚合、拉伸分离和反溅分离等现象。假设液滴为球形，二元液滴碰撞后如果反弹，那么液滴数目、大小不发生变化，只是各自的速度发生改变。

设碰撞前大液滴和小液滴速度分别为ul和us，半径分别为rl和rs，直径分别为dl和ds。在质心系中考察反弹前后液滴速度的大小［11］。碰撞前两液滴在质心系中的速度与ul和us的关系为：

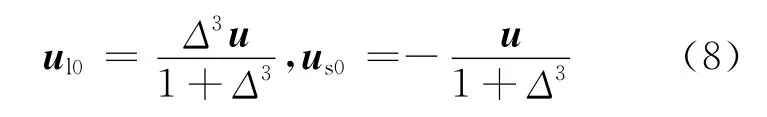
其中：u＝ul-us；ul0和us0分别为大液滴和小液滴在质心系中的速度。

假设碰撞前后动量守恒，那么在质心系中，两液滴碰撞后速度方向相反；又由于液滴间气膜作用会消耗掉一部分动能，则它们各自速率减小。因此在质心系中两液滴碰撞后的速度为：

其中：un，l0和un，s0为大液滴和小液滴碰撞后在质心系中的速度；e为恢复系数，大小为0.85［12］。

两液滴碰撞后在实验室系中的速度为：

其中，un，l和un，s为 大 液 滴 和 小 液 滴 碰 撞 后 在 实验室系中的速度（真实速度）。

二元液滴碰撞聚合成为一个新液滴，由于碰撞前后质量和动量守恒，可得新液滴的半径rn和速度un为：

拉伸分离和反溅分离的过程中会形成较小的卫星液滴，因此碰撞后计算新生成液滴的大小、速度的模型较为复杂。首先需要引入一些模型参数［9］。定义分离体积效率CVS表示二元液滴分离所需的能量和二元液滴总能量的比值，则有：

其中，Estretch、Esurten和Edissip分别为液滴的总拉伸能、总表面能和总耗散能，它们的大小分别为：

其中，α为经验常数，表示黏性耗散掉的能量占入射总动能的比值，此处假设为30%［7］。

发生分离时，可能会形成卫星液滴。卫星液滴的体积从小液滴和大液滴得到的部分分别记为ψs 和ψl，其大小分别为：

其中，φs 和φl 为体积份额系数。

当0.5（ds＋dl）（1-I）＞0.5ds时：

当0.5（ds＋dl）（1-I）≤0.5ds时：

为确定拉伸分离和反溅分离产生卫星液滴的大小和速度，做如下假设：1）若分离能产生卫星液滴，则其大小和速度相同；2）所有液滴均认为圆球状。

对于刚开始形成的卫星液滴，拉伸分离时其半径r0为：

反溅分离时r0为：

此时定义两个无量纲参数如下：

rbu的值可由下式解出：

其中，k1和k2分别为11.5和0.45［8］。卫星液滴的半径rsat由下式确定：

为确定卫星液滴和主液滴（除卫星液滴外的液滴）的最终状态，引入特征时间T：

对于拉伸分离，卫星液滴的速度usat

［9］为：

为确定卫星液滴个数nsat、碰撞后主液滴的半径rn，l和rn，s等参数，有以下选择关系：

当CVS≥0，T≤2时：

当CVS≥0，T＞2时：

以上两个关系式成立时，假设主液滴的速度与碰撞前一致，有下式成立：

其中：un，l、un，s分别为碰撞后 大 液 滴 和 小 液 滴 的速度。

但当CVS＜0时，无卫星液滴产生，因而有：

此时主液滴的速度需重新计算：

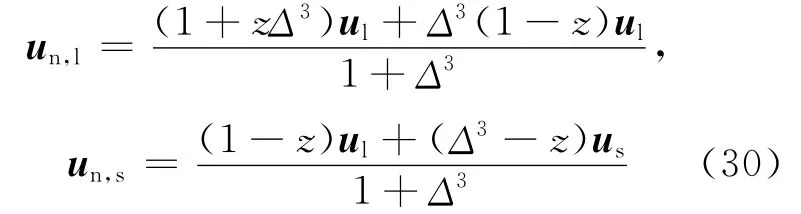
其中，z的大小由下式确定：

对于反溅分离，由于在分离过程中黏性耗散较大，主液滴的动能有所损失，因此可首先得出主液滴的速度［9］：

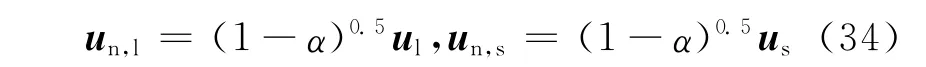
卫星液滴的速度由动量守恒定律［10］得到：）

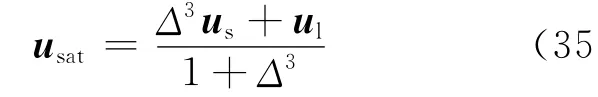
卫星液滴的个数nsat为：

上式求得的nsat不一定为整数，而卫星液滴的个数必为整数，因此需用以下选择关系式确定nsat及主液滴半径。

如果nsat＜0，有：

如果0＜nsat≤1，有：

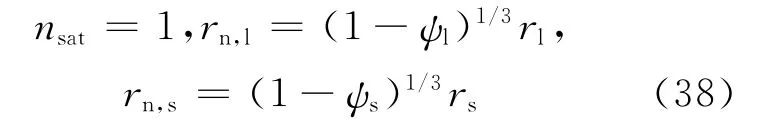
如果nsat＞1，有：

其中，［·］表示取整函数。

1、2章给出的结果统称为CZB模型。

3 模拟结果

分别采用O'Rourke模型和新建立的CZB模型模拟两股互射喷雾。喷雾示意图如图3所示，其中x 轴为水平方向，y 轴负方向为重力方向。喷雾初始参数列于表1。此外，液滴密度ρd与周围环境气体密度ρg 分别为998.23kg／m3和1.2kg／m3，液滴和气体的动力黏性系数μd和μg 分别为1.005×10-3Pa·s和1.808×10-5Pa·s。液滴与气体的表面张力系数为0.073 1N／m。

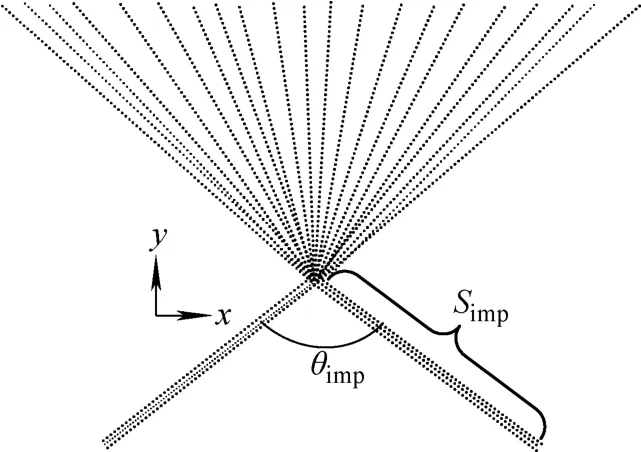
图3 两股互射喷雾示意图Fig.3 Schematic of two mutual-impingement sprays

表1 喷雾初始参数Table 1 Spray initial parameters

图4示出分别采用O'Rourke模型和CZB模型模拟所得两股互射喷雾的形态。两股喷雾相遇后的区域称为碰撞区域。对比图4a、b可知，O'Rourke 模型得到的喷雾碰撞区域较CZB模型的稀疏。同时，在整个喷雾区域外，O'Rourke模型会得到少量液滴；而对于CZB模型，此区域几乎无液滴。同时，O'Rourke模型所得喷雾碰撞区域中心位置处存在1条较为明显的液滴聚集线，而CZB 模型所得中心区域无此聚集线，而是被大量液滴覆盖。

图4 采用不同模型模拟两股互射喷雾形态Fig.4 Simulating shapes of two mutual-impingement sprays by different models

图5～7示出了喷雾左、右和下侧的局部图像。以图5 为例，O'Rourke模型得到的喷雾在左侧区域的非喷雾区存在大量液滴，这与实验图像（图8）不符。而CZB模型在左侧的非喷雾区无液滴产生，这与实验图像相符。图6、7同样可说明CZB 模型得到的喷雾在非喷雾区不会产生液滴。

图5 喷雾左侧区域比较Fig.5 Comparison of spray left zone

图6 喷雾右侧区域比较Fig.6 Comparison of spray right zone

图7 喷雾下侧区域比较Fig.7 Comparison of spray down zone

图8 两股互射喷雾的实验图像［11］Fig.8 Experimental photographof two mutual-impingement sprays［11］

综合图4～7 可知，CZB 模型模拟的喷雾较O'Rourke模型而言，能更好地反映喷雾的形态。

4 结论

本文建立了二元液滴碰撞的新型模型（CZB模型）。应用该模型模拟了两股互射喷雾的形态，得出结论如下：

1）CZB模型综合考虑了二元液滴碰撞后发生反弹、聚合、拉伸分离和反溅分离等机制，并给出了每种机制的判别准则。

2）CZB模型可计算碰撞后新生成液滴的个数、大小和速度。

3）采用CZB 模型模拟的两股互射喷雾，不会在非喷雾区域出现液滴。其模拟得到的喷雾整体形态较O'Rourke模型更接近实验值。

［1］ 林诚格.非能动安全先进核电厂AP1000［M］.北京：原子能出版社，2008.

［2］ 王琳，段永强，崔怀明.磷酸三钠在安全壳喷淋系统中的应用研究［J］.核动力工程，2011，32（2）：137-140.WANG Lin，DUAN Yongqiang，CUI Huaiming.Study on application of tri-sodium phosphate in containment spray system［J］.Nuclear Power Engineering，2011，32（2）：137-140（in Chinese）.

［3］ RABE C，MALET J，FEUILLEBOIS F.Experimental investigation of water droplet binary collisions and description of outcomes with a symmetric Weber number［J］.Physics of Fluids，2010，22：047101

［4］ O'ROURKE P.Collective drop effects on vaporizing sprays［D］.New Jersey：Princeton University，1981.

［5］ QIAN J，LAW C K.Regimes of coalescence and separation in droplet collision［J］.Journal of Fluid Mechanics，1997，331：59-80.

［6］ POST S L，ABRAHAM J.Modeling the outcome of drop-drop collisions in diesel sprays［J］.International Journal of Multiphase Flow，2002，28：997-1 019.

［7］ MUNNANNUR A，REITZ R D.A new predictive model for fragmenting and non-fragmenting binary droplet collisions［J］.International Journal of Multiphase Flow，2007，33：873-896.

［8］ KIM S，LEE D J，LEE C S.Modeling of binary droplet collisions for application to inter-impingement sprays［J］.International Journal of Multiphase Flow，2009，35：533-549.

［9］ KO G H，RYOU H S.Droplet collision processes in an inter-spray impingement system［J］.Journal of Aerosol Science，2005，36：1 300-1 321.

［10］KO G H，RYOU H S.Modeling of droplet collision induced breakup process［J］.International Journal of Multiphase Flow，2005，31：723-738.

［11］朗道，栗弗席兹.力学［M］.5版.李俊峰，译.北京：高等教育出版社，2007.

［12］BACH G A，KOCH D L，GOPINATH A.Coalescence and bouncing of small aerosol droplets［J］.Journal of Fluid Mechanics，2004，518：157-185.