基于有限元法的曲轴扭振模态分析

周 煜，孙赛龙，王昊尘

Zhou Yu，Sun Sailong，Wang Haochen

（北京航空航天大学 交通科学与工程学院，北京 100191）

曲轴是内燃机中最重要的运动部件之一，在工作过程中，曲轴的每个曲拐上都作用着大小和方向呈复杂周期变化的作用力，可能在发动机工作转速范围内发生共振，从而产生噪声和与曲轴相连齿轮系的磨损，甚至使曲轴扭断[1]。随着内燃机向轻量化和高速化方向发展，扭振成为曲轴破坏的主要原因。因此对曲轴进行扭转振动模态分析对曲轴的合理设计具有重要意义。

相关研究[2-4]在进行曲轴的模态分析时，多同时对曲轴的弯曲和扭转振动进行分析，而且很少考虑曲拐上连杆大头旋转质量的转动惯量以及活塞组、连杆小头等往复质量的等效转动惯量对曲轴固有频率产生的影响。曲轴的弯曲刚度一般很大，很少因弯曲振动引起破坏，为使研究更有针对性，文中针对某型号两缸汽油机曲轴模型的扭转振动进行了模态分析，求出各阶固有频率和振型。并对附加集中质量和未加集中质量的 2种三维有限元模型进行了对比，为曲轴的优化设计提供了参考。

1 计算模型的建立

1.1 模态分析的基本方程

用有限元方法将连续结构离散为有限个单元组成的模型，其结构的动力学平衡方程[5]为

式中，M 为总质量矩阵，C为阻尼矩阵，K为总刚度矩阵，˙˙u为加速度向量，˙u为速度向量，u为位移向量，F(t)为整体载荷向量。固有频率可以通过分析结构在无载荷时的动态响应得到，此时不考虑阻尼，式（1）简化为无阻尼的自由振动方程

由此得到特征值问题方程

式中，ω为自由振动的固有频率，φ为特征向量。求解式（3）即可求出离散模型的固有频率和相应振型。

1.2 曲轴模型基本参数

以某型号两缸二冲程汽油发动机曲轴为对象进行扭振模态分析，曲轴模型几何参数见表1。

表1 曲轴模型的几何参数

1.3 三维模型

采用整体曲轴模型，在三维实体设计软件UG中建立曲轴的三维模型，计算曲轴作为一个整体在转动方向上的自由振动特性。根据相关研究经验，在建模过程中，综合考虑有限元分析的计算工作量以及计算精度要求，对曲轴模型进行适当简化，忽略对计算结果影响不大的圆角和油道，建成的三维曲轴模型如图1所示。

进行曲轴的扭振模态分析时，除了曲轴本身各元件的转动惯量外，曲拐上连杆大头旋转质量的转动惯量以及活塞组、连杆小头等往复质量的等效转动惯量也会对曲轴扭振的固有频率产生影响。因此，采用 2种模型进行对比分析，一种为直接由 UG导入有限元分析软件中的曲轴三维模型，另一种为在导入的三维模型的基础上，在曲轴两个曲拐中心位置添加相应集中质量，如图 2所示。

1.4 有限元模型

在有限元分析软件中为模型添加材料属性，曲轴所用材料为 40Cr，该材料的主要力学性能见表2。

表2 40Cr的主要力学性能

根据曲轴模型的结构特点，选择有限元分析系统单元库中的4节点线性四面体单元C3D4对模型进行网格划分，网格数量为48340个。网格划分后模型如图3所示。

1.5 边界条件

在曲轴的模态分析中计算曲轴在无载荷时的动态响应，因此不加载任何力边界条件，只加载约束边界条件。因要分析曲轴扭转方向上的自由振动，因此限制曲轴在其他方向上的运动。建立柱坐标系，在其中约束曲轴所有节点的径向和轴向的自由度，保留其绕 Z轴旋转的自由度。添加约束后的有限元模型如图4所示。

2 模态分析结果

利用Lanczos模态分析方法，分别提取加集中质量和未加集中质量2种曲轴模型的前5阶模态。2种模型的固有频率值见表3，振型如图5～图10（仅给出前3阶）所示。

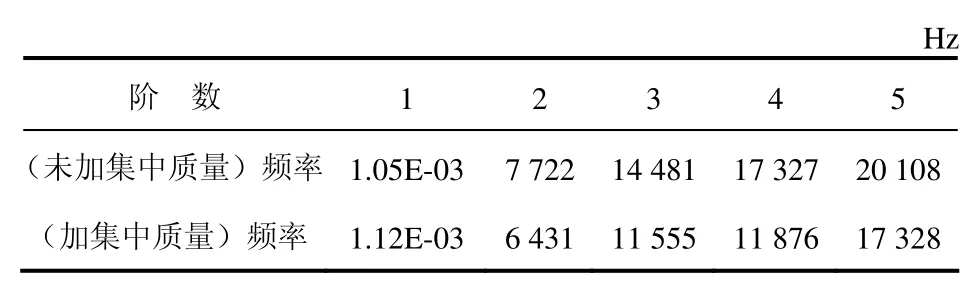
表3 曲轴模型的固有频率

由模态分析的计算结果可知，2种模型的第1阶固有频率近似为零，为转动刚体运动，可以不考虑在内，因此加集中质量和未加集中质量的 2种模型的最低扭振固有频率分别为 6431 Hz和7722 Hz。发动机的标定转速为7500 r/min，对应的频率为125 Hz。2种模型的最低阶扭振固有频率均高于发动机转速对应的频率，曲轴发生共振的可能性较小。从2种模型前5阶固有频率对比中可以看出，添加的集中质量使曲轴模型的总体质量增加，曲轴模型的固有频率值降低，各阶振型的振动型式也有所不同。2种模型的2阶振型相似，振型的节点位置位于2曲拐之间，2曲拐转动方向相反。未加集中质量曲轴的 3阶振型的节点位置位于2曲拐两侧，2个曲拐转动方向相同，而与 2曲拐间的曲柄臂转向相反；加集中质量曲轴的 3阶振型，由于曲拐处集中质量的影响，振动主要发生在曲拐两侧的曲柄臂处，曲拐振动较小。

3 结 论

针对曲轴轴系扭转振动的固有频率特性进行了有限元分析，求出其前 5阶固有频率和振型。由于其最低阶扭振固有频率高于发动机转速对应的频率，曲轴发生共振的可能性较小。

通过对加集中质量和未加集中质量 2种模型的对比分析可知，曲拐上连杆大头旋转质量的转动惯量和活塞组、连杆小头等往复质量的等效转动惯量，对曲轴扭振的固有频率有很大的影响。在对曲轴进行模态分析时，考虑活塞组和连杆的影响对模型的特定位置添加相应的集中质量，可以使计算结果更加准确。

[1]周龙保.内燃机学[M].北京：机械工业出版社，2005：299.

[2]朱发新，林少芬，陈跃坡.船舶柴油机曲轴的模态分析[J].船舶工程，2008，30（1）：23-25.

[3]吴武辉，程俊，黎水平.整体曲轴疲劳强度与自由模态有限元分析[J].机械设计与制造，2008（7）：59-61.

[4]樊晓霞，张建斌，李海刚.基于Ansys的六缸柴油机曲轴的模态分析[J].机械设计与制造，2008（9）：107-108.

[5]Hibbitt，Karlsson & Sorensen，Inc.Abaqus/Standard有限元软件入门指南[M].庄茁，译.北京：清华大学出版社，1998：165-166.