基于FP算法的电动汽车动力学协调控制

周逢军，王庆辉

Zhou Fengjun，Wang Qinghui

（北京汽车股份有限公司汽车研究院，北京 101300）

0 引 言

车辆动力学控制的目的在于提高汽车行驶的操作稳定性及安全性。在一般行驶工况下，驾驶员可通过操纵转向盘和加速/制动踏板来实现上述控制要求，但在恶劣工况下，只通过驾驶员的操作，不但会加大驾驶员操作负担，而且难以达到驾驶要求。随着汽车安全性技术需求的提高，ABS、ASR、ESP等车辆行驶稳定性控制器应运而生，因此对各种执行器进行统一协调控制分配至关重要。在车辆动力学协调控制中，控制分配的主要作用是将整车力/力矩指令信号转换成4个车轮驱动电机（冗余执行器）的转矩命令信号。控制分配方法主要分为2类[2]：基于非优化的分配方法和基于优化的控制方法。基于非优化的分配方法主要包括直接控制分配方法（面搜索算法、对边搜索算法等）和链式递增控制分配方法。直接控制分配方法由于算法复杂，计算成本高，不适于在线实时应用[1-2]，链式递增控制分配方法具有操作量大，易受执行机构速率限制等不足点[3]。基于优化的分配方法主要分为广义逆法、线性规划法、二次型规划法等。其中广义逆法只适用于目标可达的情况，当目标不可达或未知时，使用该法误差较大，同时广义逆法计算量大，实时应用性差[6]。线性规划方法需要沿着边界检验所有极点，不适合大规模控制应用[4-5]。二次型规划方法中的 FP（Fixed Point）算法是一种简单的数值算法，计算量适中，适用于实时控制分配，且算法对较小虚拟控制量的收敛速度较快[7]。因此FP算法适用于分布式驱动电动汽车的动力学协调控制分配。

在对比几种控制分配算法的基础上，首先对分布式驱动电动汽车动力学控制分配问题进行分析，建立电动车辆动力学模型，然后根据FP算法，设计分布式驱动电动汽车动力学协调控制策略，最后通过仿真对比，证明算法策略的有效性和合理性。

1 车辆建模与控制分配问题分析

分布式驱动电动汽车动力学协调控制系统架构如图 1所示。其工作原理为：根据驾驶员输入的转向盘转角、加速/制动踏板开度，得到目标纵向车速、目标侧向车速及目标横摆角速度，计算整车传感器/状态观测器反馈值与目标值的差值，根据差值计算目标纵向力、目标侧向力及目标横摆力矩，通过全局协调控制器转换成各车轮执行器的驱动力矩，以实现对整车运动状态的控制，从而保证车辆的操作稳定性及行驶安全性。

1.1 车辆建模

在车辆坐标系xoy平面内建立整车模型，模型包括7个自由度：车辆纵向运动、侧向运动、绕z轴的横摆运动、4个车轮的旋转运动。整车受力方程如下。

式中，Fx为整车纵向受力；Fy为整车侧向受力；Mz为整车横摆力矩；fl、fr、rl、rr分别为左前、右前、左后及右后车轮；δ为转向角；Bf、Br分别为前、后轮轮距；lf、lr分别为整车质心与前轴、后轴的距离。

[8]采用魔术轮胎模型，具体公式如下。

有关轮胎模型各参数的详细资料见参考文献[9]。

相比传统内燃机汽车，驱动电机具有电机力矩响应快，力矩响应精确等特点[10-11]，因此可将电机模型简化为理想模型，使用查表法输出电机的驱/制动力矩，建立模型如图2所示。

1.2 控制算法

1.2.1 控制分配协调问题分析

控制分配问题可描述为

式中，vd∈ℜm为虚拟控制量，即力/力矩；B∈ℜm×p为控制效率矩阵；U∈ℜp为控制分配解。用不动点法求解控制分配，目标函数如下

式中，Wv=diag(wv1,wv2,…,wvm)＞0，Wu=diag(wu1,wu2,…,wup)＞0为加权矩阵；ε∈(0 ,1)用来调节平衡控制分配误差和控制量。

1.2.2 控制算法设计

通过对轮胎动力学特性分析可知，轮胎纵向力（驱动力/制动力）为车轮滑移率的函数。轮胎侧向力为轮胎侧偏角的函数。因此分布式驱动电动汽车的动力学协调控制，最终可以通过分配控制算法，将目标横摆力矩Mzd、纵向力Fxd、侧向力Fyd转化成分配到各个轮胎的滑移率s、侧偏角α来实现。xyz平面上整车运动学方程为

令 x1=Vx，x2=Vy，x3=Ωz，则整车动力学系统状态空间表达式为北京汽车

将控制输入解耦分解成3个SISO（Sinble-Input Single-Output，单输入单输出）系统，具体如下

式中，v1=Fxd；v2=Fyd；v3=Mzd；wi( i=1,2,3)对应系统的外部扰动。取滑模面为反馈值与跟踪目标值之差

设计目标使 Si→ 0(i =1,2,3)。

滑膜控制律为

式中，Φi(i=1,2,3)为饱和函数；Ki(i=1,2,3)为切换增益。通过对轮胎力求导，可得控制效率矩阵为

3 仿真结果

整车模型采用的基本参数见表1，二次型优化求解时执行器约束极限见表2。

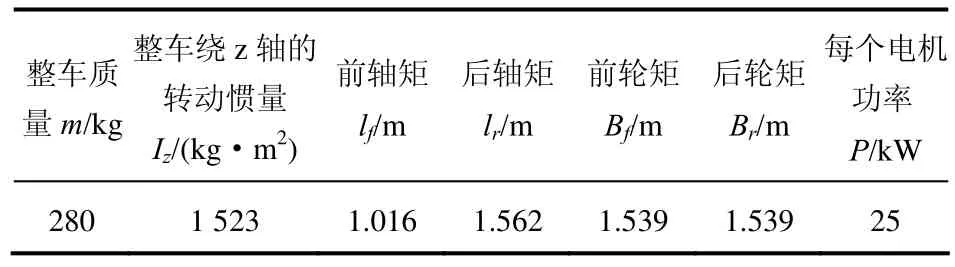
表1 整车基本参数

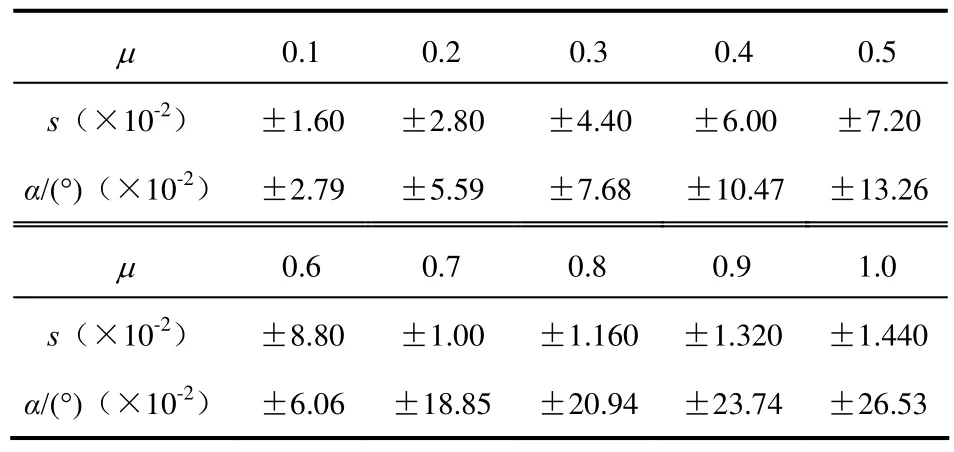
表2 控制约束极限

根据控制算法及控制分配问题分析，在Matlab/Simulink中搭建整车动力学协调控制系统模型如图3所示。

在路面附着系数为0.85、车速为120km/h条件下进行双移线仿真试验，对比FP算法控制及无算法控制，得到仿真结果如图4～图8所示。

4 结 论

将FP算法用于电动汽车冗余执行器动力学协调控制分配中，能够明显改善电动汽车轨迹保持能力及操作稳定性，同时也可以降低驾驶员驾驶强度，这对电动汽车整车动力学控制系统的开发具有重要意义，对于传统汽车动力学协调控制也具有一定的意义。

从图 4中可以看出，无控制的侧向位移与目标侧向位移最大偏差为1.3932 m，已经失控，而FP算法侧向位移与目标侧向位移最大偏差值为0.3794 m，反映了FP算法具有良好的轨迹保持能力。从图5中可以看出，经FP算法控制后的转向盘输入转角要小于无控制条件下输入转角，与后者最大偏差值为6.6174°，降低了驾驶员的驾驶强度。从图6、图7可以看出，FP算法控制的车辆横摆角速度最大值为5.5547°/s，无控制下的车辆横摆角速度为7.4063°/s，两者之间的差值为1.8516°/s；车辆质心侧偏角最大值为0.6004°，无控制下的车辆质心侧偏角为0.8005°，两者之间的差值为0.2001°，反映了FP协调控制算法能保证车辆操作稳定性。经过FP算法分配协调控制后，各个电机的力矩输入到车轮的力矩值如图8所示。

参考文献

[1]Durham W C.Constrained Controller Allocation[J].Journal of Guidance，Control and Dynamics，1993，16（4）：717-725.

[2]Ola H.Resolving Actuator Redundancy-Optimal Control Allocation[J].Automatica，2005，41（1）：137-144.

[3]Durham W C，Bordgon K A.Multiple Control Effectors Rate Limiting[J].Journal of Guidance，Control，and Dynamics，1996，19（1）：30-37.

[4]Buffington J，Chandler P，Pachter M.On-line System Identification for Aircraft with Distributed Control Effectors[J].International Journal of Robust and Nonlinear Control，1995，9（14）：1033-1049.

[5]Bodson M，Frost S A.Control Allocation With load Balancing [C].AIAA Guidance Navigation and Control Conference，2009.

[6]Bodson M.Evaluation of Optimization Methods for Control Allocation[J].Journal of Guidance，Control，and Dynamics，2002，25（4）：703-711.

[7]Fletcher R.Practical Methods of Optimization[M].2rd ed.New York：Johen Willey&Sons，2000：76-83.

[8]Bernard J E，Clover C L.Tire Modeling for Low–speed and High–speed Calculations[R]. SAE Paper1995：NO950311.

[9]Pacejka，Hans B.Tire and Vehicle Dynamics，Warrendale[M].PA，USA： MPG Books Ltd，Bodmin，Cornwall，2002：187-191.

[10]Takuya Mizushima，Pongsathorn Raksincharoensak，Masao Nagai.Direct Yaw-moment Control Adapted to Driver Behavior Recognition[C].International Joint Conference，Oct.18-21，2006，Bexco，Busan，Korea：SICE-ICASE：534-539.

[11]Motoki Shino，Masao Nagai.Independent Wheel Torque Control of Small-scale Electric Vehicle for Handling and Stability Improvement[J].JSAE Review 24（2003）：449-456.