双向双领蹄式液压鼓式制动器优化设计

胡国强，封万程，巨建辉

Hu Guoqiang，Feng Wancheng，Ju Jianhui

（中国第一汽车股份有限公司技术中心，吉林 长春 130011）

0 引 言

制动器制动效能因数是制动摩擦力与轮缸蹄端推力之比，是单位蹄端推力所产生的制动摩擦力，是评价不同结构型式制动器制动效能的指标，它表征了制动器把一定大小的制动蹄端促动力转化为制动器制动力矩进而转化为地面制动力的能力。文中选用某一带斜面支座的双向双领蹄式制动器为优化对象，以制动效能因数为优化目标[4]，利用Matlab优化工具箱代替传统设计方法，对带斜面支座的双向双领蹄式制动器进行设计计算。

1 制动器优化数学模型的建立

双向双领蹄式制动器采用 2个双活塞式制动轮缸，两制动蹄的两端都采用浮式支承，且支点的周向位置也是浮动的。制动底板上的所有固定元件，如制动蹄、制动轮缸、回位弹簧等都是成对的，而且既按轴对称又按中心对称布置。主要结构如图1所示，在张紧力Fa作用下，通过左右2个制动蹄靠紧制动鼓产生摩擦阻力矩而制动。F1为制动蹄的法向合力，R1为摩擦力μLF1的作用半径，δ1为x1轴和F1之间的夹角。其他主要位置参数有张紧力 Fa的作用线至制动器中心的距离 a、制动蹄支座销中心的坐标位置c和o。

1.1 目标函数

左领蹄制动效能因数[1]：

其中，α0为摩擦片包角，°；为α0的反三角函数(rad)；μL为衬片的摩擦系数，当前国产的制动摩擦片材料在温度低于 250℃时，摩擦系数稳定值在0.35～0.40之间，当摩擦系数超过0.4时，有可能产生制动噪声，工作稳定性变差，同时考虑到增大摩擦系数对成本的影响，文中取μL=0.35，μs为支座面摩擦系数；r为制动鼓半径；β为摩擦片中线与X轴间夹角，°；ψ为支座面与Y轴的夹角，°。

在相同的促动力下，效能因数越大，表明制动力矩越大，制动效果越好，工作效率越高。效能因数的倒数为优化的目标函数，目标函数为

其中，BF1、BF2分别为左、右领蹄制动效能因数，BF为总的制动效能因数。因双向双领蹄式制动器按中心对称布置，故BF1=BF2。

1.2 设计变量

参照目标函数，可优化的设计变量包括制动鼓半径 r，张紧力 Fa的作用线至制动器中心的距离a，制动蹄支座销中心的坐标位置c和o，摩擦片包角α0，摩擦片中线与X轴间夹角β，支座面摩擦系数μs和支座面与Y轴的夹角ψ。

引入设计灵敏度分析方法，对设计变量进行选取。设计灵敏度即设计函数对设计变量的灵敏度，表示在某设计点处设计变量的微小变化所引起的设计函数的变化程度。

设计变量的量纲不同对设计函数的影响程度不同，需要选取相对灵敏度分析方法来量化。相对灵敏度为

1.3 约束条件

1）自锁约束

在设计鼓式制动器时，必须检查蹄有无自锁的可能。

不发生自锁的条件是[2]

2）衬片表面最大压力约束

摩擦衬片上承受的最大压力应少于规定值[3]，因此有

其中，Mμ为领蹄产生的制动力矩，N·m；df为轮缸直径，mm；Pi为管路压力，MPa。

3）压力分布均匀约束

希望摩擦衬片上的压力在全长上分布均匀，该系数没有考虑摩擦力方向的影响，因此

2 优化方法

对上述数学模型进行求解，得到目标函数，即

3 计算分析

3.1 参数设定

以某车型为例，输入车辆参数：满载总质量5540 kg，满载前桥轴荷2007 kg，后桥轴荷3533 kg，车轮滚动半径363 mm，管路压力8 MPa，轮缸直径30.16 mm，制动力分配系数0.528。

汽车轮辋型号为 16吋，轮辋直径 Dr=406.4 mm，制动鼓直径D与轮辋直径Dr之比的一般范围为：货车 D/Dr=0.70～0.83，考虑到与轮辋的干涉，因此制动鼓半径取值为142≤ r≤160 mm。在保证制动轮缸能够布置于制动鼓内的条件下，应使 a尽可能小以提高制动性能，设计最小允许值根据轮缸与中心孔不发生干涉（间距L1）、拧紧制动底板的固定螺栓需要气动扳手足够的操作空间（间距 L2）等条件确定，取a≥100 mm。o的选取受到轮缸尺寸的限制，双向双领蹄制动器活塞行程S≈2×S1+b，S1为制动间隙，取0.5 mm，b为摩擦片厚度，b=9 mm，则S=10 mm，为保证活塞行程至最大值时的工作可靠性，S≤，则L≥ 20 mm，如图2所示。

两活塞间可以相互接触，即e=0，皮碗高度尺寸等设计推荐值如图 3所示；o的选取范围为o≥ 39 mm ；摩擦衬片的包角可在90°～120°范围内选取； -1 0°≤β≤10°。

3.2 设计变量灵敏度分析

该实例存在一个设计函数BF（X），7个设计变量，因此式（3）中i=1，j=7。存在3个不同的量纲，需确定相对灵敏度的取值。计算结果如表1所示。

表1 相对灵敏度计算结果

由表 1可知，r、a、o、α0和β对制动效能因数影响较大，应选取这5个变量进行优化，μs、Ψ 2个变量对制动效能因数影响较小，且约束条件中不存在此变量，故可根据变化趋势，选取合适参数值。

3.3 制动效能因数优化

优化结果如表2所示。

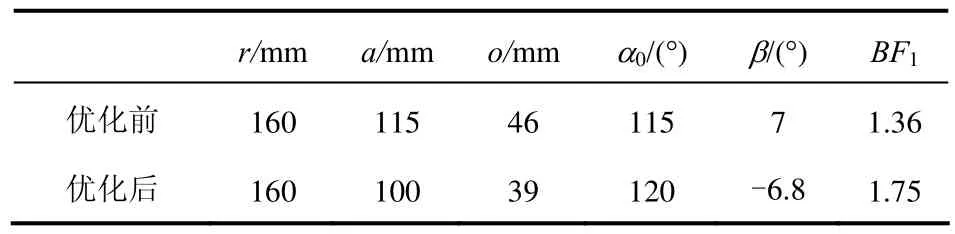
表2 优化前后参数对比

优化结果与原始数据相比，制动效能因数较优化前明显提高，制动效果更好。

3.4 单位压力特性验证

评价汽车制动器的主要性能指标是制动效能因数的数值及稳定性以及制动蹄摩擦片的使用寿命。所以需要对优化后结构参数的改变对制动稳定性及摩擦片磨损特性的影响进行分析，即对摩擦片单位压力特性进行验证。

制动蹄沿支座面的滑动基本是由蹄与鼓之间的间隙造成，这种滑动是蹄的刚体位移，不引起蹄的弹性变形，从而对蹄的压力分布没有影响，这种情况下，压力分布可用式（9）描述[2]如图5所示，最大压力点在α=90°处，制动蹄最大压力线与包角平分线间夹角

优化前 ω=atan（o/a）+β=28.8°；

优化后 ω=atan（o/a）+β=14.5°。

为了适应单位压力的分布情况，应将衬片相对于最大压力点对称布置，以改善磨损的均匀性和制动效能，因此应使夹角ω尽可能小。

对优化前后最大压力pmax和不均匀系数Δ进行对比。图6所示为优化前后最大压力与不均匀系数随β变化的趋势。由图（a）可知，优化前最大压力pmax0=1.1030；由图（b）可知，优化前不均匀系数Δ=1.3579；由图（c）可知，优化后最大压力pmax1=1.2516，稍大于优化前的值；由图（d）可知，优化后不均匀系数Δ=1.2491，小于优化前的值。β越小最大压力pmax和不均匀系数越小，即在其他结构参数已知的情况下，起始角越小，最大压力pmax和不均匀系数越小，制动稳定性越好。

通过对比优化前后制动蹄最大压力线与包角平分线间夹角，以及优化前后最大压力与不均匀系数随β变化规律，得出优化后的压力分布特性较优化前相比有所改善，磨损均匀性提高。

4 结 论

针对双向双领蹄式制动器，以制动效能因数为优化目标，通过Matlab优化工具箱，引入灵敏度分析方法，对制动器的重要参数进行了优化，并对优化后的参数进行了单位压力特性验证。优化结果表明了该设计思路的可行性，该设计思路对今后的工作具有一定的指导意义。

[1]鲁道夫L.汽车制动系统分析与设计[M].张蔚林，译.北京：机械工业出版社，1985.

[2]王霄峰.汽车底盘设计[M].北京：清华大学出版社，2010.

[3]张洪欣.汽车设计[M].北京：机械工业出版社，1999.

[4]陈克.利用 Matlab优化设计汽车鼓式制动器[J].机械设计与制造，2003（4）：18-19.