基于拉伸线法的振荡器型THz-FEL波荡器积分场测量

王艳冰 刘遐龄 秦斌 刘旭 杨磊 陈炜 刘开锋 杨军



基于拉伸线法的振荡器型THz-FEL波荡器积分场测量

王艳冰 刘遐龄 秦斌 刘旭 杨磊 陈炜 刘开锋 杨军

（华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074）

为精确、快速测量波荡器磁场积分，研制了一套基于拉伸线法的测磁系统。该系统采用Agilent 3458A八位半数字万用表实现微电压信号采集，使用Kohzu高精度位移平台实现拉伸线的精确同步移动，测量软件平台采用LabVIEW实现。使用测磁系统在一台7周期混合永磁型波荡器样机上进行了测量实验，结果同霍尔探头点测吻合，一次积分和二次积分的重复测量精度分别优于2.5´10-6T·m和2.5´10-6T·m2。该系统将用于华中科技大学在研的一套紧凑型THz波段自由电子激光装置中波荡器磁场测量。

波荡器，拉伸线法，磁场积分

华中科技大学与国家同步辐射实验室合作，目前正在研制一台振荡器型的THz波段自由电子激光装置(Huazhong University of Science and Technology THz Free-electron Laser, HUST THz-FEL)，设计相干辐射波长50-100mm（对应电子束能量8.1-11.7 MeV），峰值功率约1 MW[1-3]。波荡器是自由电子激光装置中的核心部件，作为能量“耦合器”，因其精确的周期性磁场，使得通过的电子束做横向扭摆运动，产生相干辐射电磁波。对于亚毫米波段振荡器型FEL波荡器，其参数需要根据电子束品质，在FEL引出效率和单程增益间进行平衡。HUST THz-FEL波荡器采用线性极化的铷铁硼纯永磁结构，周期数u=30，周期长度32mm，间隙可调，最小间隙16mm，值范围1.0-1.3。该波荡器在完成物理设计后，由意大利Kyma公司制造，目前已完成装配和指标验收，达到设计指标[1,4]，变间隙下相位误差<2°，一次积分与二次积分好于±5´10−6T·m和±5´10−6T·m2。

波荡器的磁场分布特性包括相位误差、积分场偏差等，对辐射光源品质起到极为重要作用。对于长波长FEL振荡器，电子束仅单次通过，影响束流工作点的多极场误差不重要。从导致闭轨畸变(Closed Orbit Distortion, COD)角度，一次、二次磁场积分也没有特别高的要求。但是由于电子束能量较低，磁场一次积分和二次积分分别决定电子束的角度和位置，需控制在较小水平。

积分场测量可采用基于霍尔探头的点测方法，以及基于拉伸线、脉冲线和翻转线圈等技术的快速测量方法[5-9]。其中，脉冲线方法虽然可测量积分场沿束流轴分布，但对Cu-Be线参数、测量环境要求很高，导致测量重复性差；而拉伸线和翻转线圈方法相对稳定，测量精度和重复性好，是一种主要的快速积分场测量方法。考虑到30周期波荡器总长为1m，包含边缘场，测量范围要求达到1.5m，超出实验室目前一台直角坐标测磁系统范围。同时为实现快速积分场测量，搭建了一套基于拉伸线的积分场测量系统。本文主要介绍拉伸线法(Stretch-wire Method, SWM)测量原理、测磁系统构架和实现方法、环境影响因素以及该测磁系统在一台7周期波荡器样机上积分场测量结果。

1 基于拉伸线的积分场测量原理

SWM最初用于四极磁铁磁场特性测量，随后在波荡器等插入件磁场测量中得到了应用[10]。该方法采用一定匝数闭合金属线，对波荡器磁场进行切割，根据电磁感应定律，将在线圈两端产生感应电压。采用不同的切割方式，将感应电压积分后可得出相应的一次和二次磁场积分[5,8-9]。

1.1 一次积分

如图1(a)所示，将处于拉伸状态的匝数为的闭合金属线圈置于波荡器磁场中，同束流轴线垂直，平行移动，保持处于磁场外面的部分固定不动，切割磁力线所产生的感应电压正比于线圈包围的磁通变化d/d。

图1 拉伸线测量一次积分(a)及二次积分(b)原理图

当线圈沿轴平行移动一个小距离d，线圈产生的感应电压对时间积分等于线圈包围磁通变化：

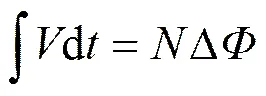
磁通的变化为：

(2)

由此得出磁场垂直分量沿轴线的一次积分为：

同理，可得出水平分量一次积分：

(4)

1.2 二次积分

如图1(b)所示，保持拉伸线一端固定，另一端向正方向运动，线圈中产生的感应电压随时间积分为：

(6)

由此，可推出二次场积分计算式：

(8)

同理，可得出水平分量二次积分：

2 SWM积分场测量系统搭建

SWM测量系统的布局如图2所示。测量拉伸线圈采用Elektrisola 50股直径80mm的利兹线串联绕制。由于绞合线单股线径太细，焊接难以控制，极易造成短路及虚焊，为此设计了电路板以加强各股线的连接。

图2 拉伸线积分场测磁系统原理图

在波荡器两端安装了日本Kohzu公司的两套水平方向和垂直方向的线性运动平台(XA10A-L2/ ZA16A-X1)，该平台集成了5相步进电机和编码器。运动控制器选用Kohzu SC410 4轴控制器，内含电机驱动器，可实现最多三轴同步控制。驱动器带有细分脉冲技术，该技术可以减弱或消除步进电机的低频振动，提高电机的运转精度。采用二十细分之后，水平和垂直方向运动精度分别为0.2mm和0.1mm。结合运动控制器与两套二维运动平台，可实现水平方向或垂直方向的高精度同步移动，重复定位精度达到±2mm。对于移动速度，结合感应电压输出要求及噪声的抑制，对一次和二次积分的测量分别取2mm·s-1和6mm·s-1。

感应电压的测量采用实验室已购置的安捷伦3458A八位半数字万用表，当设置NPLC=1（采样率50Hz）时，设置电压量程0.1V，分辨率可达到10nV，远小于背景噪声1mV。

考虑到在测量时需要同时控制位移平台和电压测量装置，采用了GPIB总线串联SC410和3458A，连接至控制笔记本。使用LabVIEW编写了测量控制软件系统，控制程序从功能上可分为运动控制、数据采集两部分。运动控制部分可对线性运动控制器SC410的运行速度、测量的起始点和位移、运动模式等进行设定。数据采集通过对3458A的远程控制，采集直流电压信号并进行积分。为简化系统，未采用硬件触发方式，而是利用LabVIEW软件触发进行运动和电压测量的时序控制。

图3为搭建的拉伸线积分场测磁系统，为验证测量精度，对一台7周期波荡器进行了测试。该波荡器长度260mm，周期32mm，固定间隙16mm，采用混合型结构，由于未安装端部垫补线圈，积分场较大。

图3 基于拉伸线圈法的积分场测量系统

3 测量数据分析

3.1 霍尔探头测量法(Hall Probe Method, HPM)

为比对参照，采用HPM对7周期波荡器样机进行了磁场测量。受霍尔点测装置范围限制，测量纵向长度仅取860mm，但波荡器两端边缘场区域达到300mm，认为已降低至地磁水平。为对点测数据进行修正，单独测量了地磁轴向分量，约0.2Gs。而在对波荡器点测时，将背景磁场置零。测量了波荡器横向=0mm、=-5mm、=+5mm处纵轴长860mm的磁场，重复测量5次，并以此为依据计算出波荡器一二次积分。图4为=0mm时波荡器样机磁场分布。

图4 霍尔探头点测磁场分布

3.2 SWM

为减少实验误差、提高测量的准确性和验证实验的重复性，我们在不同的日期对一次积分和二次积分分别进行了三组实验测量，每组实验进行20次测量。图5(a)、(b)分别为=0mm两端平行移动时一次积分电压及电压积分信号，测量速度为2mm·s−1。图6为=0mm单端移动时二次积分电压及电压积分信号，测量速度为6mm·s−1。图5、6显示了其中5次测量数据。图7为一、二次积分随的变化曲线图。表1为SWM和HPM测量一次积分和二次积分的结果。

图5 一次积分电压(a)及电压积分(b)信号

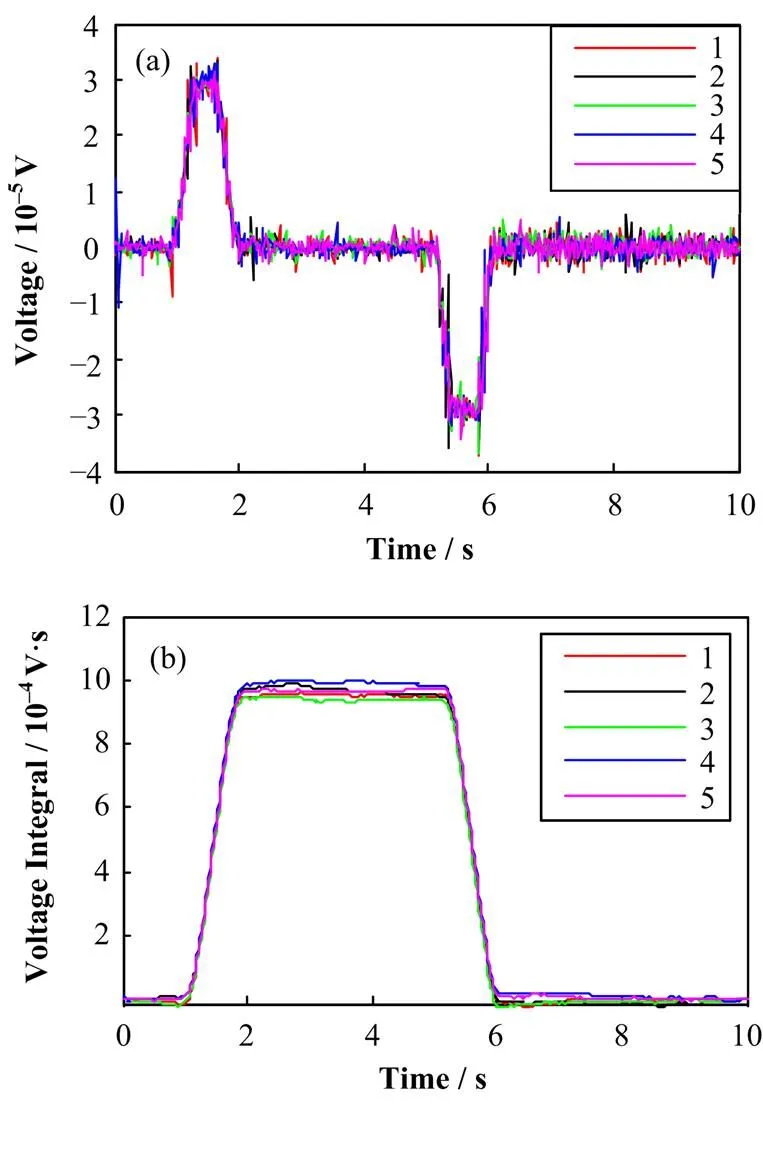
图6 二次积分电压(a)及电压积分(b)信号

图7 一次积分(a)、二次积分(b)随x的变化曲线

表1 拉伸线法与霍尔探头积分结果对比(Iy / 10−6T·m，IIy/ 10−6T·m2)

在拉伸线法测磁系统中，拉伸线长度取110cm，考虑到拉伸线法导线的有效测量长度比霍尔探头测量范围长，对霍尔点测数据进行了修正，即增加了地磁轴向分量在拉伸线长度的影响，约为0.2´110=22Gs·cm。对点测数据进行修正后，两种方法的测量结果吻合。

4 测量结果的干扰因素及处理

SWM具有系统搭建相对简单、积分场测量快速等优点，但是由于所产生感应电压较弱，测量结果易受环境干扰，需要仔细分析若干干扰因素并进行处理，以获得较高的重复测量精度。

4.1 感应电压的测量

SWM的关键就是获取相对准确的感应电压。对于小的磁场积分，感应电压较弱，通常在微伏量级，因此提高测量系统的信噪比成为一个主要问题，可通过下述两方面解决。

4.1.1 提高拉伸线圈感应

根据式(3)和(8)，一次及二次磁场积分的感应电压同拉伸线圈匝数和移动速度成正比，的选取由所测量磁场积分的重复测量精度、电压积分测量精度及环境噪声决定，本实验装置采用=50的设置。更大的匝数可提高测量精度，但对于极细的利兹线串联焊接带来了困难。线圈的移动速度需要考虑过大时带来的线圈振动噪声，因此结合信号增益需要取一个平衡值，通过实验，对一次和二次积分测量分别取2mm·s−1和6mm·s−1。

4.1.2 降低感应电压背景噪声

影响感应电压的噪声有如下因素[8,11]：(1) 拉伸线圈的振动对获取感应电压的干扰，虽然电机的运动速度越快得到的感应电压越大，但是电机的运行速度、线的张紧程度等因素产生的驻波是影响线的振动的主要因素，采用细分脉冲数的方法控制电机的运行速度和增加线的张力，可以减小线的振动，特别在拉伸线上放置橡皮对较小线的振动具有明显效果；(2) 日光灯产生的电磁干扰也会对测量设备产生影响，关灯前后背景噪声相差为3.5mV，相对于测量电压，占据了相当大的比重；(3) 测量设备本身存在随机误差和本底误差也会对测量电压产生影响，利用拉伸线来回运动可消除所产生本底误差。

4.2 测量二次积分时导线的切割方式

在进行二次积分测量时，导线的切割运动方式对测磁结果也产生影响。除了§1.2介绍的单端运动方式以外，还有一种两端相对运动方式[10]。我们对两种方法进行了实验比较：当两端相对移动时，电机的运动带来的线圈振动较大，同时，相向对称运动带来了磁通变化的抵消，感应电压很小，导致信噪比过低；而对于相同的二次积分场和移动速度，单端移动的感应电压幅值约为两端相对运动方式的4倍。因此，选择了单端切割运动的方式。

5 结语

精确快速测量波荡器磁场的一次积分和二次积分，对于波荡器的垫补、调试和运行有重要意义。本文介绍了SWM测量积分场的基本原理，对基于该方法的积分场测量系统的搭建、影响测量结果因素的分析与处理进行了详细阐述。使用拉伸线测磁系统在一台7周期混合永磁型波荡器样机上进行了测量实验，结果同霍尔探头点测数据吻合，一次积分和二次积分的重复测量精度好于2.5´10-6T·m和2.5×10−6T·m2。该系统将用于华中科技大学在研的一套紧凑型THz波段自由电子激光装置中波荡器磁场测量，为变间隙下波荡器校正线圈的设计提供依据。

1 Qin B, Tan P, Yang L,. Design considerations of a planar undulator applied in a terahertz FEL oscillator[J]. Nuclear Instruments and Methods in Physics Research, 2013, A727: 90−96. DOI: 10.1117/12.2182164

2 Pei Y J. Design of 14 MeV linac for THz source based FEL[C]. The 4thInternational Particle Accelerator Conference, Shanghai, 2013

3 Tan P. Optical cavity losses calculation and optimization of THz FEL with a waveguide[C]. The 4thInternational Particle Accelerator Conference, Shanghai, 2013

4 秦斌. HUST THz-FEL波荡器及其积分场测量系统[C]. 第二届中国粒子加速器会议(CPAC 14), 武汉, 2014 QIN Bin. Undulator and field measurement system in HUST THz-FEL[C]. Chinese Particle Accelerator Conference (CPAC 14), Wuhan, 2014

5 Wolf Z. Undulator field integral measurements[R]. SLAC-TN-10-076, SLAC National Accelerator Laboratory, US, 2005

6 Tripathi S, Gehlot M, Hussain J K,. Field integral measurement of a six period undulator in a pulsed wire set up[J]. Optics Communications, 2011, 284: 350-357. DOI: 10.1088/1748-0221/9/01/T01002

7 王宏飞, 陆杰, 周巧根, 等. 翻转线圈系统在波荡器积分场测量中的应用[J]. 强激光与粒子束, 2008, 22(4): 871-875 WANG Hongfei, LU Jie, ZHOU Qiaogen,. Flipping coil system application in the undulator integral field measurement[J]. High Power Laser and Particle Beams, 2008, 22(4): 871-875

8 汪涛. 插入件积分场测量装置研制及相关技术研究[D].合肥: 中国科技大学, 2009 WANG Tao. Development of field integral measurement facilities and research on related technology of insertion devices[D]. Hefei: University of Science and Technology of China, 2009

9 王宏飞, 张继东, 周巧根. 精确测量波荡器磁场的伸展线磁测系统[J]. 核技术, 2009, 32(9): 653-656 WANG Hongfei, ZHANG Jidong, ZHOU Qiaogen. The stretch-wire system for accurate measurement of the undulator magnetic field[J]. Nuclear Techniques, 2009, 32(9): 653-656

10 Zangrando D, Walker R P. A stretched wire system for accurate integrated magnetic field measurements in insertion devices[J].Nuclear Instruments and Methods in Physics Research, 1996, A776: 275-282. DOI: 10.1016/0168-9002(96)00207-0

11 刘遐龄. 太赫兹FEL波荡器磁场分析及积分场测量技术研究[M]. 武汉: 华中科技大学, 2014 LIU Xialing. Magnetic field analysis of an undulator applied in THz-FEL oscillator and research on field integral measurement facility[M]. Wuhan: Huazhong University of Science & Technology, 2014

Integral magnetic field measurement of THz-FEL oscillator undulator based on stretch-wire method

WANG Yanbing LIU Xialing QIN Bin LIU Xu YANG Lei CHEN Wei LIU Kaifeng YANG Jun

(State Key Laboratory of Advanced Electromagnetic Engineering and Technology, Huazhong University of Science & Technology, Wuhan 430074, China)

Background: In collaboration with the National Synchrotron Radiation Laboratory, Huazhong University of Science and Technology is developing an oscillator-based THz free-electron laser (HUST THz-FEL). Purpose:In order to measure the magnetic field integrals of the undualtor accurately and quickly, a measurement system based on the stretch-wire method (SWM) was established.Methods: In the system, an eight and a half digital multimeter, Agilent 3458, was adopted to acquire the micro-volt voltage signal, and a Kohzu high precision positioning platform was employed to realize the high synchronized wire movement. The software of this system was implemented by LabVIEW programming Results:The field measurement system was tested in a prototype hybrid permanent undulator with 7 periods, which shows consistent results with the Hall probe mapping. The repeatability precision for first integral and second integral are better than 2.5´10-6T·m and 2.5´10-6T·m2respectively. Conclusion:The system met the design requirements and will be applied to the compact THz FEL oscillator located in Huazhong University of Science and Technology.

Undulator, SWM, Magnetic field integral

TL503.8

TL503.8

10.11889/j.0253-3219.2015.hjs.38.070103

国家自然科学基金(No.11375068)资助

王艳冰，男，1991年出生，2014年毕业于华中科技大学，现为硕士研究生，从事波荡器装置研究

秦斌，E-mail: bin.qin@mail.hust.edu.cn

2015-01-15，

2015-02-06