BP神经网络在DNBR计算中的应用

黄禹 刘俊强 刘乐



BP神经网络在DNBR计算中的应用

黄禹 刘俊强 刘乐

（深圳中广核工程设计有限公司上海分公司 上海 200241）

在压水堆事故分析中，通常采用系统分析程序、热流密度计算程序和子通道分析程序分步计算堆芯偏离泡核沸腾比(Departure from Nucleate Boiling Ratio, DNBR)。利用该方法计算的堆芯DNBR结果准确性较好，但是计算过程繁琐、费时。对于系统分析程序自带的堆芯DNBR简化计算模型，由于其根据堆芯限制线偏微分近似得到，适用范围较窄，准确性也难以保证。利用神经网络中的误差反向传播(Back Propagation, BP)算法，基于堆芯核功率、入口温度、流量和压力4个变量对应的一系列DNBR值，选取部分数据进行训练并建立模型，以达到快速和准确地预测堆芯DNBR的目的。根据误差分析，建立的计算模型具有较好的准确性，而且在部分失流事故和汽机停机事故下可较好地预测堆芯DNBR。

偏离泡核沸腾比，神经网络，误差反向传播算法，事故分析

偏离泡核沸腾(Departure from Nucleate Boiling, DNB)是压水堆核电厂安全分析中的一个重要参数，一旦发生DNB就有可能导致燃料棒烧毁，所以核电厂实际运行中，应避免发生堆芯DNB。反映实际运行中距离堆芯DNB的程度一般采用偏离泡核沸腾比(Departure from Nucleate Boiling Ratio, DNBR)来表示，因此在核电厂实际运行中，监测或预测堆芯最小DNBR对于防止燃料棒烧毁是非常重要的。另外，在II类设计基准事故以及部分III类事故下将堆芯最小DNBR是否满足验收准则作为事故分析结果是否通过的判据，因此建立一套快速和准确预测堆芯DNBR的方法具有重要意义。

在20世纪80年代中期，形成了一股神经网络的研究热潮，目前在核电领域，特别是核电站故障诊断以及堆芯参数预测等方面有较多的研究[1–4]。黄彦平等[3]根据圆管临界热流密度(Critical Heat Flux, CHF)实验数据，建立了一套基于人工神经网络的圆管CHF预测系统，其预测精度要好于其它几种常规方法的预测结果。武俊梅等[4]通过建立预测CHF的人工神经网络模型来分析压力、流量、热平衡含汽率和进口过冷度对CHF的影响。考虑到在堆芯在线监测以及事故分析中堆芯DNBR是重要参数，目前国外也有较多关于堆芯DNBR分析方法的研究[5–9]，主要关注不同算法以及拓扑结构对预测结果的影响，其中包括的算法有误差反向传播(Back Propagation, BP)、支持向量回归(Support Vector Regression, SVR)、模糊支持向量回归(Fuzzy Support Vector Regression, FSVR)和模糊神经(Fuzzy Neural, FN)等算法，部分研究取得了较好的预测效果。Kim等[5]通过BP网络，建立了瞬态堆芯DNBR计算模型，训练数据主要集中在额定功率附近，对于轴向功率分布固定的模型取得了较好的预测结果。但是，对于堆芯轴向功率分布不固定的模型，预测误差较大。Na等[8]根据模糊神经网络，建立了堆芯最小DNBR监测模型，通过与实际核电厂堆芯运行限值监测系统(Core Operation Limit Supervisory System, COLSS)的数据进行比较，显示该模型具有一定准确性，误差稍大的地方主要在于COLSS对于热棒的功率分布假设较保守导致。

本文的工作内容主要是基于AP1000压水堆核电厂的设计参数，根据系统程序计算的堆芯参数（核功率、入口温度、压力和流量）以及子通道程序计算的堆芯DNBR结果，对单隐层BP神经网络进行训练和测试，经过训练后的数据即可根据系统程序计算的4个堆芯参数直接计算堆芯DNBR。通过对部分失流和汽机停机事故的瞬态堆芯DNBR结果[10]进行预测发现，所训练的模型能够准确地预测在事故情况下的瞬态堆芯DNBR。本文所提供的训练数据在较宽的功率和流量范围内，它覆盖了15%–120%额定功率以及反应堆冷却剂失流的情况，消除了系统分析程序中简化堆芯DNBR计算模型适用范围较窄的限制，可适用于失流等事故的瞬态堆芯DNBR计算分析。

1 计算模型

1.1 BP算法

BP神经网络[11–12]由Rumelhart等在1986年提出，它是目前应用最广泛的神经网络模型之一，它是一种按误差逆传播算法训练的多层前馈网络。BP网络能学习和存储大量的输入输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络拓扑结构包括输入层、隐层和输出层，输入层和输出层一般为一层，隐层可以有一层或以上的层数，每一层中的变量称为一个神经元，单隐层BP神经网络如图1所示。

图1 单隐层BP网络结构图

对于单隐层网络，BP算法学习过程如下：

网络输入向量P=(1,2,…,a)；

网络目标向量=(1,2,…,y)；

隐层输入向量=(1,2,…,s)，输出向量=(1,2,…,b)；

输出层输入向量=(1,2,…,l)，输出向量=(1,2,…,c)；

输入层至隐层的连接权W，=1, 2,…,，=1, 2,…,；

隐层至输出层的连接权V，=1, 2,…,，=1, 2,…,；

隐层各神经元的输出阈值，=1, 2,…,；

输出层各神经元的输出阈，=1, 2,…,；

参数=1, 2,…,。

利用输入样本、连接权w和阈值计算隐层各神经元的输入s，用s通过传递函数计算隐层各神经元的输出 b。

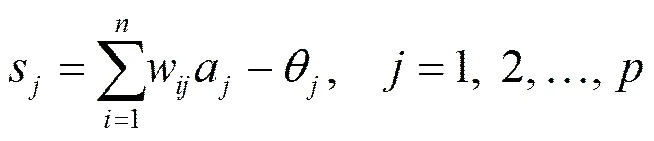
(2)

利用隐层输出b、连接权v和阈值γ计算输出层各神经元的输入l，用l通过传递函数计算输出层各神经元的输出c。

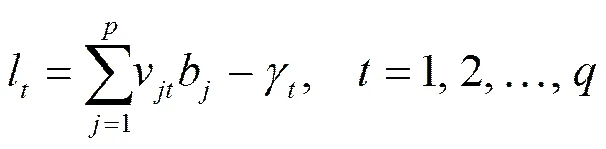
(4)

利用网络目标向量=(1,2,…,y)和网络实际输出c，计算输出层各神经元一般化误差d。

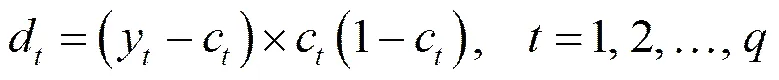
利用连接权v、输出层的一般化误差d和隐层的输出b计算隐层各神经元的一般化误差e。

(6)

利用输出层各神经元的一般化误差d与隐层各单元的输出b来修正连接权v和阈值。

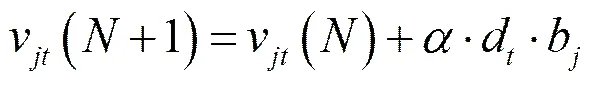
(8)

式中，=1, 2,…,，=1, 2,…,，0<<1。

利用隐层各神经元的一般化误差e，输入层各神经元的输入P=(1,2,…,a)来修正连接权w和阈值。

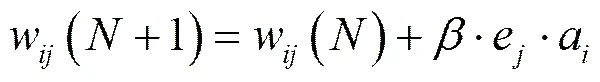
(10)

式中，=1, 2,…,，=1, 2,…,，0<<1。

通过这种正向计算输出和反向传播误差的多次迭代，直到计算误差达到期望值，同时获得一组稳定的权值和阈值。

1.2 数据取样

考虑到文中所建立的堆芯DNBR预测模型主要为安全分析使用，可假设建模所采用的子通道分析模型计算数据准确，建模数据主要分训练数据和预测数据两部分。为提高模型的预测性能，训练数据的选取适当考虑各变量之间合理搭配，并且尽可能扩大变量的范围。考虑在压水堆核电厂安全分析中，对部分II类设计基准事故而言，堆芯径向和轴向功率分布可采取保守考虑，为确保所建模型的准确性及稳定性，本分析仅考虑了以下4个变量：核功率、入口温度、压力和流量，各变量的数据范围详见表1。

表1 输入及输出参数范围

1.3 预测模型建立

本文的预测模型采用含有一个隐层的BP神经网络，各层神经元个数分别为4-8-1，输入和输出层神经元个数根据分析的问题决定，隐层中神经元个数则无固定要求，可根据训练时间以及收敛程度决定，一般需要进行试算或实验。网络结构的选取原则应尽量使结构简单且具有较强的泛化能力。单隐层培训误差下降速度较双隐层快，在精度达到要求的前提下可选择较少的隐层数，对于BP网络应有一个最佳隐层神经元数。训练算法采用Levenberg-Marquardt，该算法对于加快BP网络的收敛速度有较大好处。输入层及隐层传递函数为transig函数，输出层为线性函数。

文中根据100个稳态DNBR数据进行训练，采用均方误差(mean square error, mse)训练性能函数，由图2看出，在经过58次训练后mse值下降到1.1697×10−5，它表明所建立的分析模型较好。

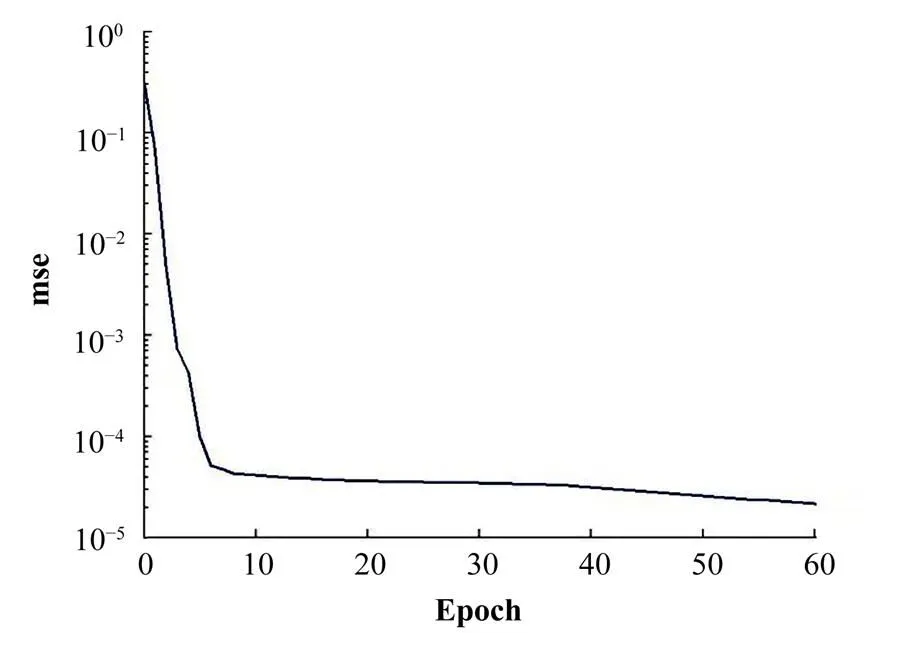
图2 训练误差收敛曲线

2 堆芯DNBR预测及结果分析

根据训练后的BP网络预测模型，本文搜集了文献[10]中多个事故的数据，共计591个数据点进行预测，BP网络预测值(BP Prediction DNBRs)和子通道分析值(Subchannel Results)之间的预测误差结果详见表2，其中单侧95/95误差限为6.4%，图3显示了数据点的分布和比较情况。图4对所有数据点的误差分布进行了统计，发现误差分布基本满足正态分布要求。

表2 预测误差结果Table 2 Results of prediction error.

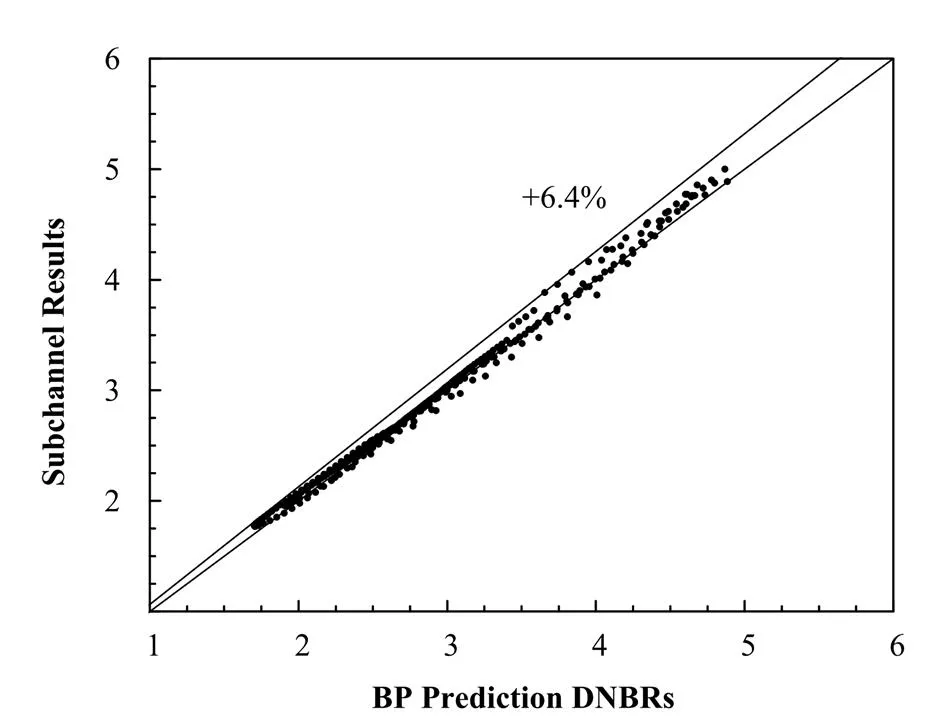
图3 预测结果

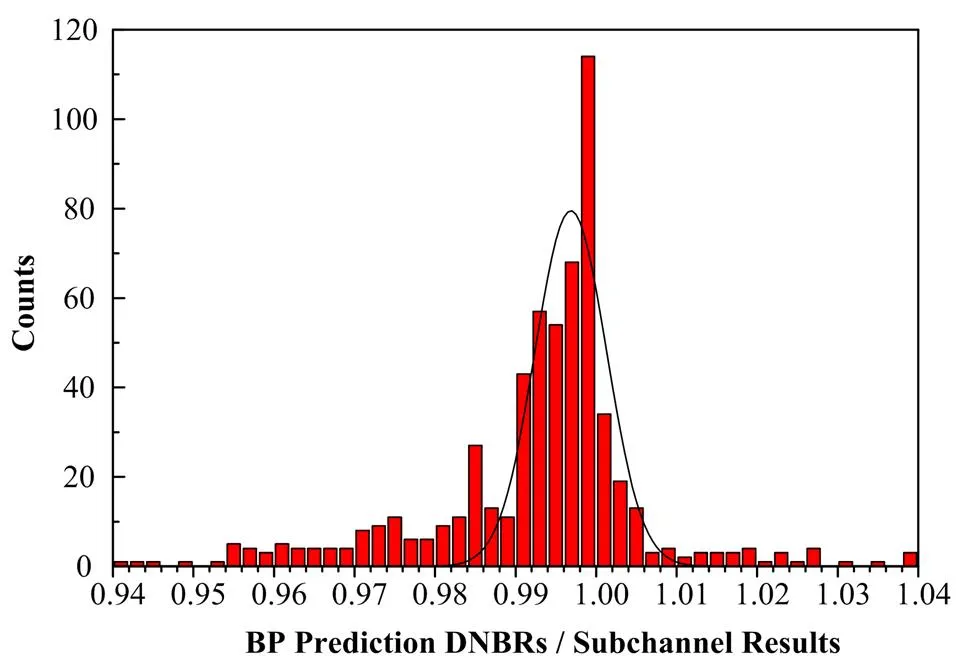
图4 预测误差统计

本分析对事故下的瞬态堆芯DNBR进行了预测，图5和6分别对文献[10]中部分失流事故和汽机停机事故下的堆芯DNBR结果进行了比较，无论是瞬态堆芯DNBR变化趋势还是数值大小，BP网络预测结果与子通道分析值都很接近。另外，在图6中还将BP网络预测结果与系统程序自带的堆芯DNBR计算结果进行了比较，发现系统程序自带计算结果与子通道分析值之间有较大偏差，而BP网络预测结果相对较好。

图5 部分失流事故堆芯DNBR预测

图6 汽机停机事故堆芯DNBR预测

3 结语

本文根据子通道分析程序的计算数据建立单隐层BP神经网络，训练后的网络模型在事故下堆芯DNBR预测中显示了较好的预测能力，计算误差较小。与系统分析程序自带的堆芯DNBR简化计算模型相比，BP神经网络预测的趋势和数值都较好。若将该模型植入于系统分析程序中，可较快地查看在事故中的瞬态堆芯DNBR的分析结果。就其准确性而言，预测值具有一定的参考价值。

1 刘永阔, 夏虹, 谢春丽, 等. 核电设备状态监测与故障诊断系统的研究[J]. 原子能科学与技术, 2008, 42(3): 200–205 LIU Yongkuo, XIA Hong, XIE Chunli,. Research on state monitoring and fault diagnosis system of nuclear power equipment[J]. Atomic Energy Science and Technology, 2008, 42(3): 200–205

2 谢春丽, 夏虹, 刘永阔, 等. BP神经网络改进算法在核电设备故障诊断中的应用[J]. 核动力工程, 2007, 28(4): 85–90. DOI: 10.3969/j.issn.0258-0926.2007.04.020 XIE Chunli, XIA Hong, LIU Yongkuo,. Application of improved BP algorithm in fault diagnosis of nuclear power equipment[J]. Nuclear Power Engineering, 2007, 28(4): 85–90. DOI: 10.3969/j.issn.0258-0926.2007.04.020

3 黄彦平, 单建强, 陈炳德, 等. 人工神经网络在圆管临界热流密度数据分析中的应用研究[J]. 核科学与工程, 2003, 23(1): 45–51. DOI: 10.3321/j.issn:0258-0918.2003.01. 008 HUANG Yanping, SHAN Jianqiang, CHEN Bingde,. Application of artificial neural networks in analysis of CHF experimental data in tubes[J]. Chinese Journal of Nuclear Science and Engineering, 2003, 23(1): 45–51. DOI: 10.3321/j.issn:0258-0918.2003.01. 008

4 武俊梅, 苏光辉. 临界热流密度的人工神经网络预测法[J]. 核动力工程, 2007, 28(1): 41–44. DOI: 10.3969/ j.issn.0258-0926.2007.01.010 WU Junmei, SU Guanghui. Prediction of critical heat flux by using artificial neural network[J]. Nuclear Power Engineering, 2007, 28(1): 41–44. DOI: 10.3969/j.issn. 0258-0926.2007.01.010

5 Kim H C, Chang S H. Development of a back propagation network for one-step transient DNBR calculations[J]. Annals of Nuclear Energy, 1997, 24(17): 1437–1446. DOI: 10.1016/s0306-4549(97)00051-0

6 Koo B H, Kim H C, Chang S H. Development of real-time core monitoring system models with accuracy-enhanced neural networks[J]. IEEE Transactions on Nuclear Science, 1993, 40(5): 1347–1354. DOI: 10.1109/23.234549

7 Lim D H, Yang H Y, Na M G. Monitoring minimum DNBR using a support vector regression model[J]. IEEE Transactions on Nuclear Science, 2009, 56(1): 286–293. DOI: 10.1109/tns.2008.2009216

8 Na M G, Lee S M, Shin S H,. Minimum DNBR monitoring using fuzzy neural networks[J]. Nuclear Engineering and Design, 2004, 234: 147–155. DOI: 10.1016/j.nucengdes.2004.08.022

9 Lee S W, Kim D S, Na M G. Prediction of DNBR using fuzzy support vector regression and uncertainty analysis[J]. IEEE Transactions on Nuclear Science, 2010, 57(3): 1595–1601. DOI: 10.1109/tns.2010.2047265

10 AP1000 design control document (Rev.19)[R]. Westinghouse Electric Company, 2011

11 飞思科技产品研发中心. 神经网络理论与MATLAB7实现[M]. 北京: 电子工业出版社, 2005 The Research Center of Feisi Science and Technology. Theory of neural network and MATLAB 7 application[M]. Beijing: Publishing House of Electronics Industry, 2005

12 丛爽. 面向MATLAB工具箱的神经网络理论与应 用[M]. 合肥: 中国科学技术大学出版社, 2009 CONG Shuang. Neural network theory and applications with MATLAB toolboxes[M]. Hefei: Press of University of Science and Technology of China, 2009

Application of BP neural network in DNBR prediction

HUANG Yu LIU Junqiang LIU Le

(,.,.(),,)

Background:In safety analysis of pressurized water reactor (PWR), departure from nucleate boiling ratio (DNBR) is usually calculated by three codes: a system transient analysis code, a heat flux calculation code and a subchannel analysis code, or by simplified model through a partial derivative approximation of the core DNB limit lines, but either procedure has problems of cumbersome or low accuracy.Purpose:The aim of this study is to gain a simple DNBR calculation method with high accuracy.Methods:A 3-layers back propagation (BP) neural network was proposed with a training data set to quickly predict DNBR using four variables of reactor coolant system (nuclear power, core inlet temperature, mass flow rate and pressure).Results:The error of the developed BP network is very small, and has similar results compared with the subchannel code calculations in two typical events. Conclusion:The trained BP network is accurate enough to be used in predicting DNBR, even in transient conditions.

DNBR, Neural network, BP algorithm, Accident analysis

TL33

TL33

10.11889/j.0253-3219.2015.hjs.38.070606

黄禹，男，1986年出生，2010年于上海交通大学获硕士学位，反应堆热工水力

2015-02-10，

2015-03-09