基于载波和空间矢量调制之间联系的多电平VSI降低和消除共模电压的PWM策略

佘阳阳 杨柏旺 吴志清 李王敏 姜卫东

（合肥工业大学 合肥 230009）

1 引言

自1981年日本长岗大学教授Akira Nabae提出三电平结构[1]以来，三电平结构已在高压（中压）电机交流传动、电网无功补偿和吸收、FACTS和电网质量管理等多个领域得到广泛应用。与传统的两电平结构相比，三电平结构具有如下的优点：①每个功率管承受的电压为直流侧的一半；②在相同的开关频率下，输出波形的谐波分量大幅降低；③每个功率管开通和关断时，器件开关损耗降低[2,3]。

在某些应用场合，例如在交流传动中，往往需要降低共模电压（Common Mode Voltage, CMV），避免轴电流对于电机的损坏，并且降低电磁干扰[4-6]。按照文献[7-10]中的观点，当电机采用PWM控制的电压源逆变器供电时，主要有三种共模电流产生：①当润滑油膜被破坏以后，电机定转子之间等效电容的放电作用；②当轴电流通路的等效阻抗较低时，共模电压的dv/dt的作用；③电机三相零序电流分量导致电机磁通产生三相环流。

目前降低共模电压方法的研究主要集中于：①在逆变器输出端添加有源或者无源共模滤波器[11-13]；②采用软开关技术或者改善器件的吸收电路，从而降低逆变器输出的 dv/dt[11]；③对硬开关电路改变PWM 调制策略[15,16]。在工程应用中，往往需要低成本且易于实现的解决方案，改变PWM调制策略不会增加新的器件，因此改变 PWM调制策略的解决方案最具吸引力。

现已有多种控制策略可应用于多电平逆变器的控制中，最为广泛的是空间矢量 PWM 调制策略（Space Vector PWM，SVPWM）和基于载波的PWM调制策略（Carrier Based PWM，CBPWM）。已有研究表明[17,18]，当CBPWM和SVPWM之间满足一定关系时，这两者具有相同的频谱特征。由于CBPWM本质比较简单且易于实现，因而被广泛应用于多电平逆变器的调制算法中。

在CBPWM和SVPWM调制中，如何降低共模电压，已有文献进行了研究，但大多针对的是NPC三电平逆变器，少有文献将算法扩展到多电平逆变器。另外，这些研究成果中没有明确地给出给定参考电压（或者空间电压矢量）与能够降低共模电压矢量之间的关系。本文中，针对任意奇数电平的逆变器，提出了降低和消除共模电压的调制策略。并通过 Matlab仿真和实验，对所提出的算法加以验证。

2 NPC三电平逆变器拓扑与SVPWM算法

图1a为NPC三电平逆变器的电路拓扑，分压电容电压取自两路独立的直流电源，中点电位不需要控制，避免了利用冗余电压矢量对中点电位进行平衡控制时，造成对算法的影响。每相有四个功率管，分别为 S1、S2、S3、S4，当 S1、S2导通时，输出1电平；当S2、S3导通时，输出0电平；当S3、S4导通时，输出-1电平。

图1 三电平NPC VSI的电路拓扑结构和空间矢量图Fig.1 Topology and space vector of three level NPC VSI

每相均可输出三个电平，一共有 27个空间矢量，用三维有序数组(ka,kb,kc)表示。矢量(ka+1,kb+1,kc+1)和矢量(ka,kb,kc)是一对冗余矢量，对负载来说效果是一致的。独立矢量个数为19（含零矢量），三电平逆变器的空间矢量图如图1b所示，空间矢量图在0～60°扇区（A扇区），被分为4个小三角形，如图1c所示。

将逆变器的调制度采用线电压定义，定义为

式中，VL为逆变器输出线电压的有效值，V6,step为逆变器6步方波调制时相电压峰值，且V6,step=4VDC/π，VDC为直流母线单电源电压[19]。在线性调制区内，SPWM的最大调制度为0.785；SVPWM的最大调制度为0.907。

当参考矢量的方位角θ∈ [ 0,π/3]时，参考矢量位于A扇区内，三电平逆变器的空间矢量算法可以分为三步进行，①确定参考矢量位于的小三角形，选择该小三角形的三个顶点对应的电压矢量来合成参考矢量V*；②计算电压矢量的作用时间；③安排电压矢量作用的序列。当参考矢量位于 A3三角形内时，合成参考矢量的电压矢量选择V1、V2和V7：

式中，T为控制周期；t1为V1的作用时间，t2为V2的作用时间，t7为V7的作用时间。由于V1对应两个电压矢量V1,1(0, -1, -1)和V1,2(1,0,0)，V2矢量也对应两个电压矢量V2,1(0,0,-1)和V2,2(1,1,0)。中央对称的 SVPWM策略（CSVPWM），要求将矢量作用时间对称的分配给两个冗余矢量，并以冗余矢量作为过渡，产生的脉冲序列如图2所示。

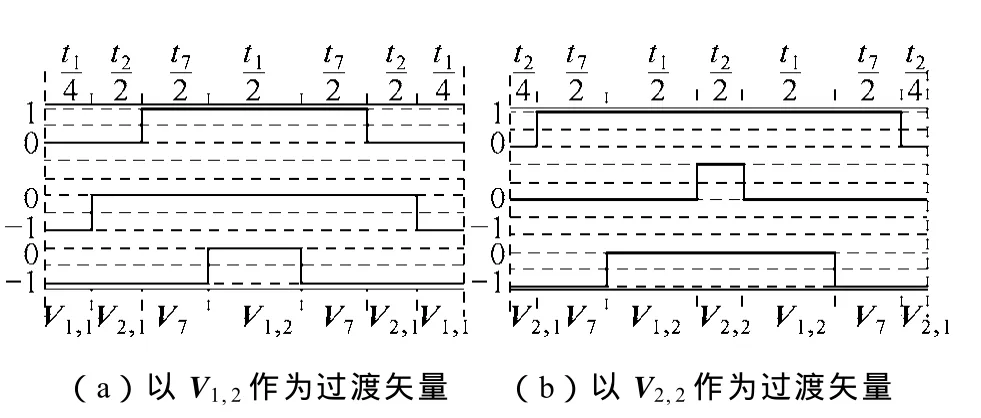
图2 CSVPWM在A3三角形内的序列脉冲Fig.2 The pulse sequences of CSVPWM in A3triangle

3 部分共模电压减小的PWM算法（PCMVPWM）

逆变器输出的每个电压矢量的共模电压Vcom可采用下式计算得到。

在A扇区内每个电压矢量对应的共模矢量见下表。

表 A扇区内每个电压矢量对应的共模电压Tab. The common mode voltages of each voltage vector in A sector

3.1 合成参考矢量的电压矢量选择

在三电平逆变器的空间矢量调制中，V0、V1、…、V6存在冗余，选择适当的电压矢量，可将共模电压降低到DC/3V±。当选择矢量(0,0,0)实现V0，选择矢量(1,0,0)实现V1时，图2所对应的脉冲序列如图3所示。从图3中可看出，B相在该采样周期内无开关动作，开关损耗有所降低。PCMVPWM具有如下特点：①开关损耗降低，在一个采样周期内开关次数降低了三分之一；②由于采用了最近相邻三矢量合成原则（NTV），谐波特性相对较好。

图3 PCMVPWM在A3三角形内的脉冲序列Fig.3 The pulse sequences of PCMVPWM in A3 triangle

3.2 PCMVPWM与CBPWM的联系

除了指定谐波消去 PWM 算法（SHEPWM），其余 PWM算法都存在采样周期的概念，均为次谐波消除PWM算法（Sub-harmonic PWM，SHPWM），所有SHPWM算法都可等效为调制信号为非正弦的载波 PWM算法，载波周期等于控制周期。在一个采样周期内，三相调制Va、Vb、Vc满足

则有ka+kb+kc=-1或者ka+kb+kc=-2。再令

当ka+kb+kc=-1时，

图4 PCMVPWM和CSVPWM等效的调制波Fig.4 The equivalent modulation waveforms of PCMVPWM and CSVPWM

4 完全共模电压消除PWM算法（FCMVPWM）

若进一步限制矢量选择的条件，PCMVPWM算法可以转换为FCMVPWM算法。选择V0,2、V7、…、V12合成参考电压矢量，如图5所示。

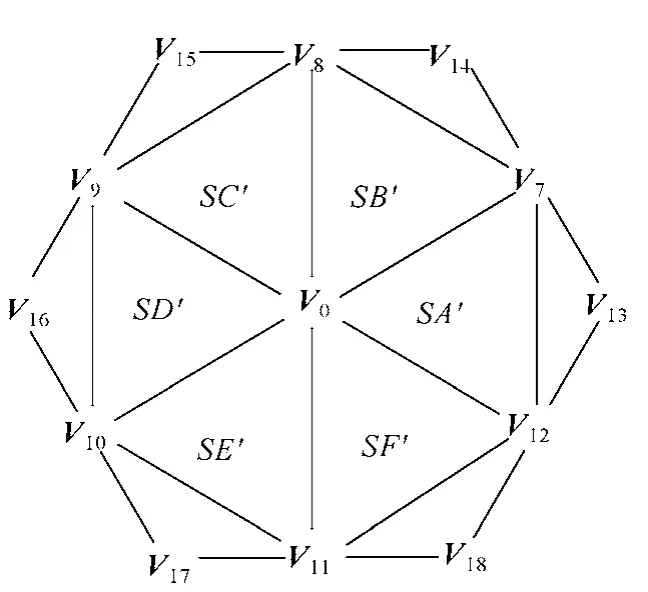
图5 三电平VSI FCMVPWM的空间矢量图Fig.5 The three level VSI space vector of FCMVPWM

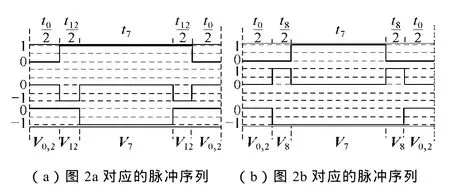
图6 FCMVPWM在A3三角形内的脉冲序列Fig.6 The pulse sequences of FCMVPWM in A3 triangle

5 FCMVPWM与CBPWM的联系

多电平逆变器的载波产生方式大多出自于Carrara等提出的载波移位（carrier disposition）法[20]。FCMVPWM 与 CBPWM 的联系可以通过变换载波与调制波的关系获得，一个采样周期内，取Vx=max(Va,Vb,Vc)，Vy=min(Va,Vb,Vc)。假定 a相电压最高，C相电压最低，B相电压处于中间，对应的双调制波为

任何一相输出的 PWM波形为对应两个调制波与载波比较之和，如图7所示，与图6a的序列是完全一致的。其余5种情况分析类似。FCMVPWM的调制度受到最高电压和最低电压的限制，在线性调制区内最大调制度为0.785。

图7 双调制波及其脉冲序列Fig.7 Double modulation waveforms and pulse sequences

6 算法的仿真与实验

6.1 仿真结果与分析

为了验证算法的有效性，在Matlab/Simulink平台上建立了系统仿真模型，通过仿真验证和分析CSVPWM、SPWM、PCMVPWM和FCMVPWM算法的线电压、相电压、共模电压的特点。仿真参数VDC=100V，载波比为24。仿真结果如图8所示。

6.2 实验验证

为了验证算法的有效性，搭建了NPC三电平逆变器原型机。功率器件为2MBI400N－060 IGBT，钳位二极管为 2FI200A－060D，直流侧电容为2 200μF。TMS320C2812 DSP完成系统的采样和输出矢量的时间计算，为了保证所有驱动信号的同步，采用 FPGA EPM7128ElC8420作为驱动信号的分配部分。图9是整个控制系统的控制框图和原型机照片。逆变器输出频率为 50Hz，调制度m为0.75，每周期采样24次，逆变器输出电流峰值为1.9A。

图8 仿真结果Fig.8 The simulation results

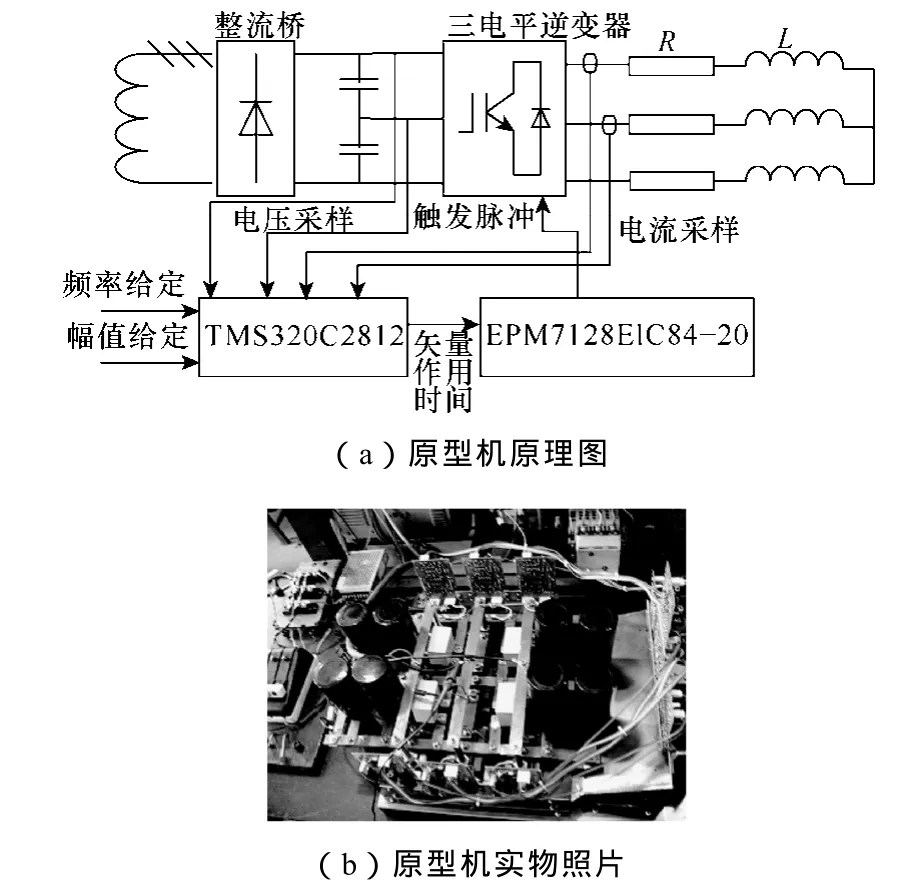
图9 实验室原型机结构图与实际系统照片Fig.9 Laboratory prototype structure diagram and photo

为了能够克服死区时间对调制策略的影响，采用文献[21]所提出的死区补偿方法，将每个采样周期内的三相PWM补偿为对称的PWM波形。比较图10和图11，可看出SVPWM和SPWM两种调制策略在线电压、相电压、电流和共模电压方面的特性是非常相似，这种相似源于两者均采用了七段合成的最近相邻三矢量合成原则（NTV）。PCMVPWM能将共模电压降低到±VDC/3，从图12a中可以看出，此时电流还是比较平滑的。FCMVPWM 调制方法能够完全消除逆变器输出的三相共模电压，但是电流谐波含量有所增高，这是由于FCMVPWM采用的不是NTV矢量合成方式。总的来说，NTV矢量合成方式优于NNTV矢量合成方式[22,23]。

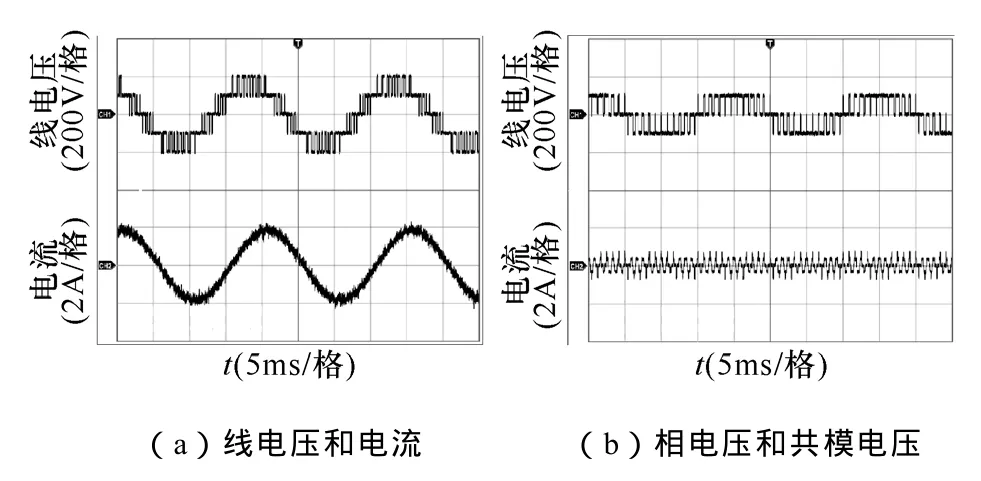
图10 SPWM调制时的实验结果Fig.10 The experimental results under SPWM

图11 SVPWM调制时的实验结果Fig.11 The experimental results under SVPWM

图12 PCMVPWM调制时的实验结果Fig.12 The experimental results under PCMVPWM

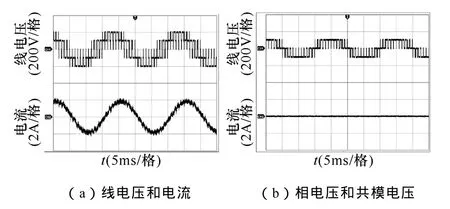
图13 FCMVPWM调制时的实验结果Fig.13 The experimental results under FCMVPWM

7 算法向更多电平的推广

二极管钳位型N（N为奇数）电平逆变器的拓扑如图14所示，从式（4）～式（7）的证明过程（见附录）可知，对任意电平逆变器，上述四式所产生的调制波仍可降低共模电压。

图14 二极管钳位型N电平逆变器电路拓扑Fig.14 Topology of diode clampedN-level inverter

当采用载波反相层叠法的双三角波双载波调制时，按照式（9）的方法给出双调制波，FCMVPWM可以不加任何修正的应用到N（N为奇数）逆变器的调制中。

PCMVPWM 的调制度范围为min(0.907,0.785+0.525N- 1)，而FCMVPWM的电压利用率为0.785。因此三电平逆变器 PCMVPWM 调制时电压利用率等于SVPWM的电压利用率0.907，而在FCMVPWM调制时电压利用率等于SPWM的电压利用率0.785。

8 结论

本文主要介绍了一种三电平逆变器降低共模电压的调制方法。分析了PCMVPWM和FCMVPWM的调制方法，并讨论了这两种算法与CBPWM之间的本质联系，这种联系可以简化 PWM脉冲产生计算，将基于空间矢量调制简化为基于载波的调制。仿真与实验结果表明PCMVPWM能够局部降低共模电压，FCMVPWM能够完全消除共模电压。最后，将该算法推广到任意电平逆变器的控制中。

附录：式（4）～式（7）的证明

已知Va+Vb+Vc=0 ，根据式（4）有kaVDC++kbVDC++kcVDC+=0 ，化简为

因为VDC＞≥0，所以-3＜ (ka+kb+kc)≤0，ka+kb+kc取值为0、-1、-2。当取值为0时，共模电压为零。

当ka+kb+kc=-1时，假设式（5）中Vn=，则

A相输出电平始终为ka，B相输出为kb、kb+1，C相输出为kc、kc+1，则根据式（3）有Vcom=-VDC/3、0、VDC/3。其他两种情况与此类似推导。

当ka+kb+kc=-2 时，设式（5）中Vp=VDC-，则

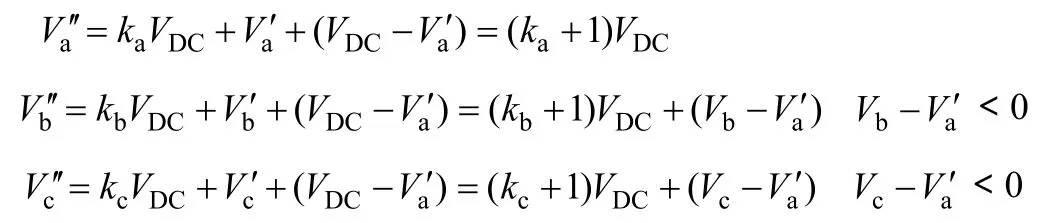
A相输出电平始终为ka+1，B相输出为kb、kb+1，C相输出为kc、kc+1，则根据式（3）有Vcom=-VDC/3、0、VDC/3。其他两种情况与此类似推导。

[1] Nabea A, Takahashi I, Akagi H. A new neutralpoint-clamped PWM inverter[J]. IEEE Transactions on Industrial Application, 1981, IA-17(5): 518-523.

[2] Teichmann R, Bernet S. A comparison of three-level converters versus two-level converters for lowvoltage drives, traction, and utility applications[J].IEEE Transaction on Industry Applications, 2005,41(3): 855-865.

[3] Newton C, Sumner M. MuIti-level convertors, a real solution to medium/high-voltage drives[J]. Power Engineering Journal, 1998, 12(1): 21-26.

[4] 钟玉林, 赵争鸣. 改进式 SHEPWM 对三电平变频器系统的共模电压和轴电压的抑制作用[J]. 电工技术学报, 2009, 24(6): 48-55.

Zhong Yulin, Zhao Zhengming. Common mode voltage and shaft voltage suppression on a three-level NPC inverter system applying improved SHEPWM[J].Transactions of China Electrotechnical Society, 2009,24(6): 48-55.

[5] 刘铮, 王翠, 彭永进, 等. 级联多电平逆变器空间矢量调制算法零序电压分布及优化算法[J]．电工技术学报, 2008, 23(12): 92-98.

Liu Zheng, Wang Cui, Peng Yongjin, et al. Zero order voltage distribution and optimized algorithm of SVPWM method for multi-level cascaded inverter[J]. Transactions of China Electrotechnical Society, 2008, 23(12):92-98.

[6] 姜艳妹, 刘宇, 徐殿国, 等. PWM 变频器输出共模电压及其抑制技术的研究[J]. 中国电机工程学报,2005, 25(9): 47-53.

Jiang Yanshu, Liu Yu, Xu Dianguo, et al. Research on Common-mode voltage generated by a PWM inverter and its cancellation technology[J]. Proceedings of the CESS,2005, 25(9): 47-53.

[7] Chen Shaotang, Thomas A Lipo. Modeling of motor bearing current in PWM inverter drives[J]. IEEE Transaction on Industrial Application, 1996, 32: 1365-1370.

[8] Chen S, Lipo T A. Bearing currents and shaft voltages of an induction motor under hard and soft switching inverter excitation[C]. IEEE Transactions on Industry Application, 1998, 34(5): 1042-1048.

[9] S Chen, Lipo T A, Fitzgeraid D. Source of induction motor bearing currents caused by PWM inverters[J].IEEE Transaction on Energy Conversion, 1996, 11(1):25-32.

[10] S Chen, Lipo T A, Novotny D W. Circulating type motor bearing current in inverter drives[C]. IEEE Industry Application Society Annual Meeting, 1996:162-167.

[11] Akagi H, Doumoto T. An approach to eliminating high-frequency shaft voltage and ground leakage current from an inverter-driven motor[J]. IEEE Transactions on Industry Application, 2004, 40(4): 1162-1169.

[12] Chen X, Xu D, Liu F, et al. A novel inverter-output passive filter for reducing both differential- and common-mode dν/dtat the motor terminals in PWM drive systems[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 419-426.

[13] Mei C, Balda J C, Waite W P. Cancellation of common mode voltages for induction motor drives using active method[J]. IEEE Transactions on Energy Conversion, 2006, 21(2): 380-386.

[14] H Xiangning, A Chen, W Hongyang, et al. Simple passive lossless snubber for high-power multilevel inverters[J]. IEEE Transactions on Industry Electronics,2006, 53(3): 727-735.

[15] Cacciato M, Consoli A, Scarcella G, et al. Reduction of common mode currents in PWM inverter motor drives[J]. IEEE Transactions on Ind. Appl. , 1999,35(2): 469-476.

[16] Kim H J, Lee H D, Sul S K. A new PWM strategy for commonmode voltage reduction in neutral point clamped inverter-fed AC motor drives[J]. IEEE Transactions on Industry Application, 2001, 37(6): 1840-1845.

[17] Bowes S R, Lai Y S. The relationship between spacevector modulation and regular-sampled PWM[J]. IEEE IEEE Transactions on Industry Electronics, 1997,44(5): 670-679.

[18] Zhou K, Wang D. Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis[J]. IEEE Transaction on Industrial Electronics, 2002, 49(1): 186-196.

[19] 张兴, 杜少武, 黄海宏. 电力电子技术[M]. 北京:科学出版社, 2010.

[20] G Carrara, S Gardella, M Marchesoni, et al. A new multilevel PWMmethod: A theoretical analysis[J].IEEE Transaction on Power Electronics, 1992, 7(3):497-505.

[21] Dongsheng Zhou, Rouaud D G. Dead-time effect and compensations of three-level neutral point clamp inverters for high performance drive applications[J].IEEE Transactions on Power Electronics, 1999, 14(4):782-788.

[22] Brendan P M, Donald G H, Thierry M. Reduced PWM harmonic distortion for multilevel inverters operating over a wide modulation range[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 941-949.

[23] Gupta A K, Khambadkone A M. A space vector PWM scheme for multilevel inverters based on two-level space vector PWM[J]. IEEE Transaction on Industrial Electronics, 2006, 53(5): 1631-1639.