基于空间直角坐标系的逆变器调制波研究

卢远宏 郑琼林 马 亮

（1. 北京交通大学电气工程学院 北京 100044 2. 北京京仪绿能电力系统工程有限公司 北京 100009）

1 引言

空间矢量调制（SVPWM）与正弦脉宽调制（SPWM）这两种调制方法具有各自的优缺点。SVPWM有电压利用率高、易于数字化[1-4]、运算量小和谐波畸变少等优点[5-8]，SPWM具有易于硬件实现、计算简单和易于建模等优点，但其电压利用率比SVPWM低约15%。通过分析SVPWM和SPWM方法之间的内在关系，建立了两者的统一调制函数表达式[9,10]，基于零序空间矢量基本函数确定的零序分量，建立从载波角度研究SVPWM的新方法，具有计算简单、易于实现的优点[11-14]。但这些研究主要基于abc三相平面坐标系[15]、αβ两相静止平面坐标系[16]和 dq两相旋转平面坐标系，均为二维平面坐标系，对于调制波本身尤其是其零序分量没有直观的几何表示。还有一些文章都用到了空间坐标系研究电压[17-19]，但其建立的并不是数学上常用的3轴正交的空间直角坐标系，而是 4轴耦合空间坐标系，研究对象也为3P4W系统。文献[15]提出abc坐标下对SVPWM算法实现方法进行了研究，避免了αβ和dq坐标变换，计算简单快速，有一定参考价值。

本文第一部分建立空间直角坐标系xyzO，提出三维空间调制波矢量的概念和研究方法，将三相调制波分别作为三维矢量的三个坐标，在空间直角坐标系中研究其运行轨迹和分布范围，可以直观得到调制波零序矢量的物理含义。计算过程无需坐标变换，简化了计算过程。

本文的第二部分对调制波矢量允许添加的零序范围做了计算，添加不同的零序矢量，可以分别得到SPWM和SVPWM的解析表达式，使调制方法与控制策略及硬件建模成为一个解析的整体，便于分析研究。对于任何调制波矢量，均有其相对的零序矢量范围，可给出判断过调制的条件。

本文的第三部分，讨论了添加不同的零序矢量分析对SVPWM的影响，并利用Matlab仿真和分析。第四部分对仿真进行硬件实验。

2 三维矢量表示三相物理量

2.1 构造空间直角坐标系

构造空间直角坐标系xyzO，以三相电网电压为例，将三相电压分别作为空间直角坐标系中矢量E的三个坐标，设定E为理想的正弦波形，满足

以解析几何角度理解，式（1）表示以t为参变量的空间曲线参数方程，容易推出以x、y、z为变量的空间曲线方程

定义正负序平面 ∏pn:x+y+z=0 ，垂直于法向量 (1,1,1)=n。对任意一个三维矢量，均可分解为三个分量即正序、负序、零序矢量，其中正序与负序位于∏pn上，零序垂直于∏pn，平行于n。

由空间解析几何定理易得，矢量分解

正负序矢量

零序矢量

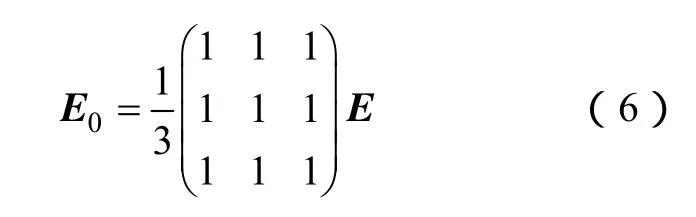
圆周C、E、Epn、E0、n与∏pn的空间位置如图1所示。

图1 三维矢量在空间直角坐标系中的表示Fig.1 3D vector in space Cartesian coordinate system

2.2 3P3W逆变器的三维矢量建模

3P3W下逆变器电路如图2所示。以Sk（k=a,b,c)表示上、下桥臂的状态为

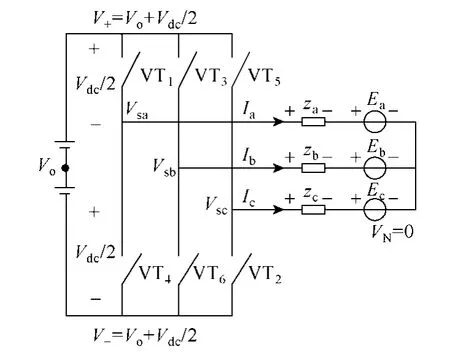
图2 3P3W下逆变器电路Fig.2 Three phases two levels inverter curcuit

则桥臂电压满足

设上桥臂开通时间为Ton，关断时间为Toff，对

式（8）在一个开关周期内积分得

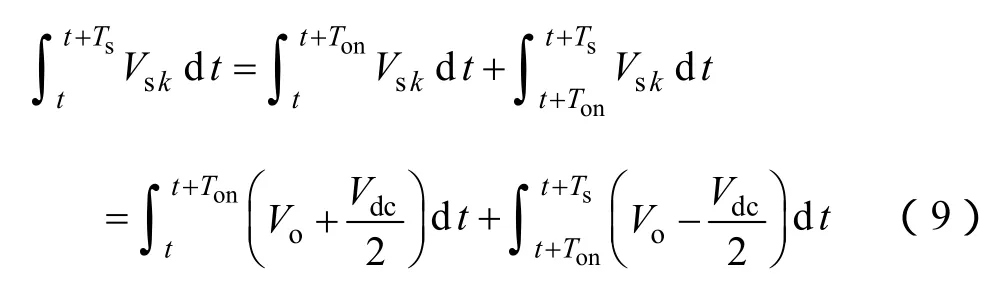
式（9）等号两边同时除以Ts得

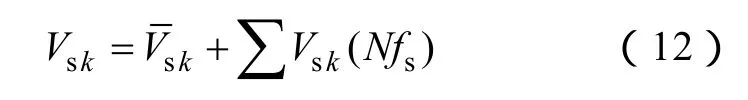
考虑开关频率较高情况下，高频分量很小，本文仅分析低于开关频率次的分量，所以忽略高次谐波得

定义瞬时调制波Dk(k=a ,b,c)如下

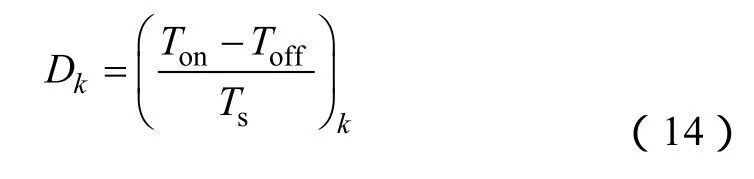
则易得

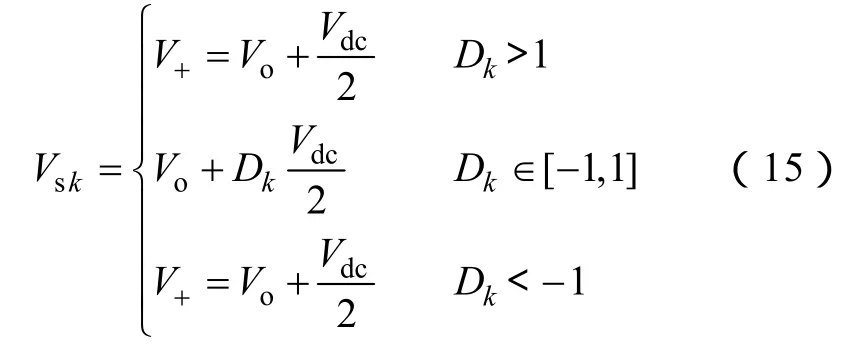
从式（15）看出，当Dk超出区间[-1,1]范围时，Vsk波形出现畸变，不再和Dk保持线性关系，无法有效利用直流电压，发生过调制。所以Dk∈[- 1 ,1]为不发生过调制的条件。

与式（1）类似，定义D为调制波矢量。

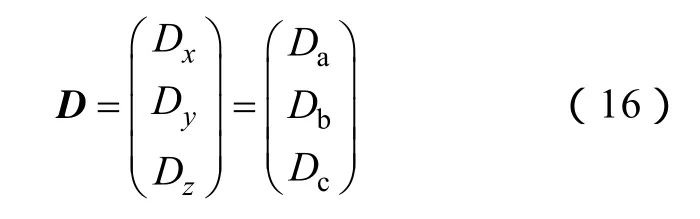
对图2逆变器进行三维矢量数学建模，将桥臂相电压Vsk，阻抗两端电压VZk，电网相电压Ek，负载电流Ik这些三相物理量均用三维矢量表示，令交流中性点电压VN为参考电压零点，则交流侧存在

对于3P3W系统，存在约束条件

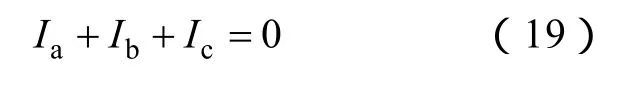
式（19）与式（6）联立得

直流侧存在以下等式

构造零序矢量

不发生过调制情况下，对式（15）进行矢量化

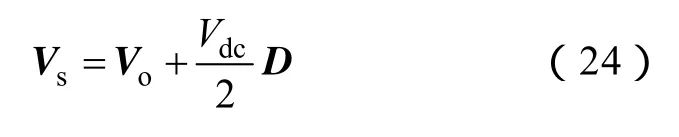
将式（5）和式（6）代入式（24）得

由式（17）和式（18）可得

式（6）分别代入式（27）等号两边得

将式（20）代入式（28）得

特殊地，E=零或者平衡情况下

将式（29）、式（30）代入式（24）得

综上，三个坐标独立的三维矢量有E和D，而只含有正、负序矢量的有Vs和I。式（31）表明，Vs本身不含有零序矢量，与正、负序矢量有关而与D的零序矢量无关。所以可以通过控制Dpn来控制Vs。

2.3 调制波矢量的空间几何分布特点

在不发生过调制的情况下，调制波矢量的三个坐标均属于[-1,1]区间，所以调制波矢量分布在图3中 ABCDEFGH 8个顶点所确定的空间正方体内，将正方体按A-O-G方向投影到正负序平面∏pn的投影图，如图4所示。

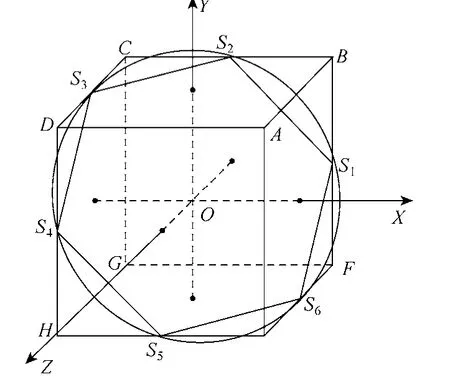
图3 调制波矢量的空间几何分布Fig.3 Distribution of modulation wave vector space rectangular coordinate system

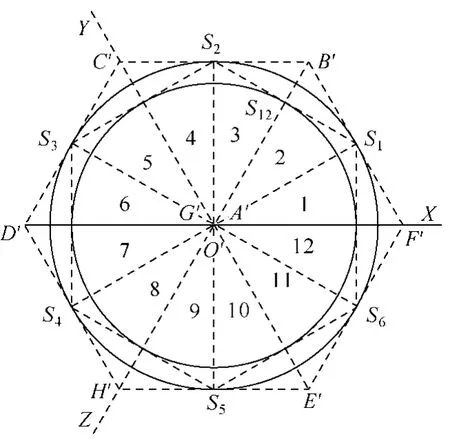
图4 正方体在正负序平面的投影Fig.4 The projection of the cube in the plane of positive and negative sequence

所述正方体具有如下特点：

（1）正方体六个面的方程分别是x=±1 ,y=± 1 ,z=±1，正方体的中心位于原点，并关于三个坐标轴中心对称。

（2）正方体的8个顶点坐标见表1。

（3）正方体与正负序平面相交的截面是正六边形，称之为“截面正六边形”，如图4所示，此六边形的顶点为S1、S2、…、S6，依次平分线段FB、BC、CD、DH、HE、EF，各点坐标见表。

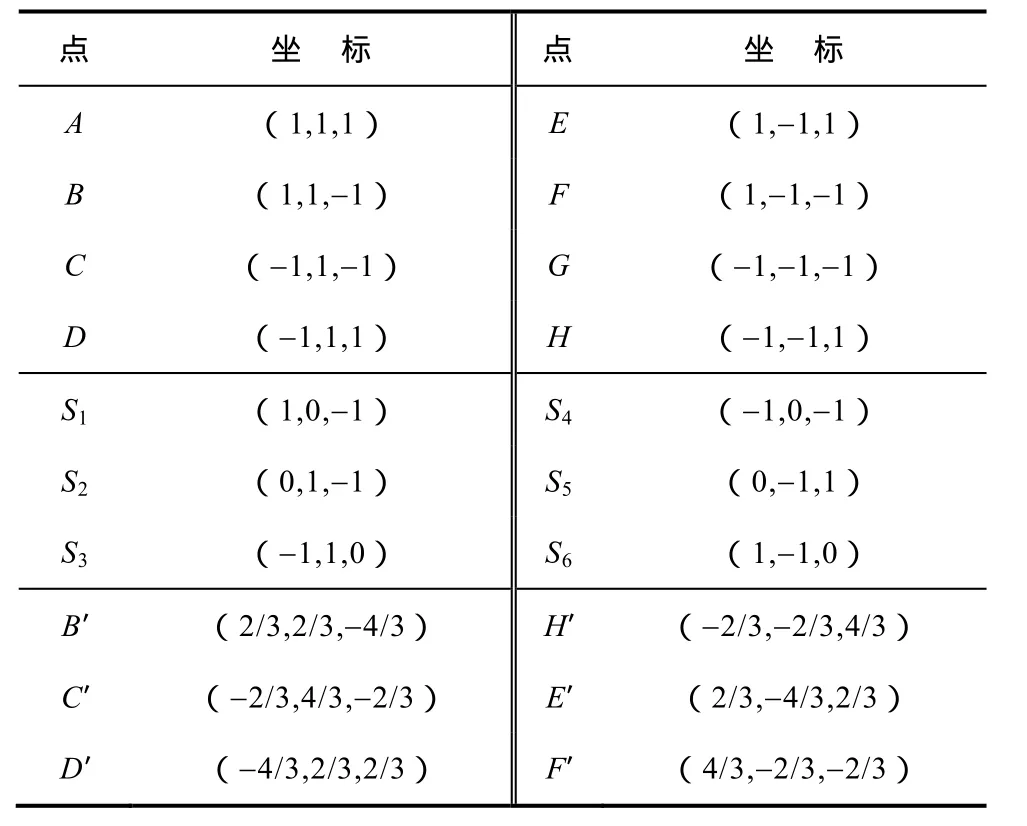
表 空间正方体中各点的坐标Tab. The vertex coordinates of the cube

（4）将正方体向正负序平面投影，投影图形的外轮廓线也是正六边形，称之为“投影正六边形”，如图4所示。六边形顶点坐标见上表。

（5）截面正六边形外接圆与投影正六边形内切圆相同；投影正六边形内切圆半径为，截面正六边形内切圆半径为/2，两圆半径比值为2/=1.154 7。

2.4 SPWM与SVPWM的空间几何表示

下面讨论调制波矢量的正负零序与调制方法的关系。如图5，取调制波空间正方体纵截面AGB：

图5 调制波空间正方体的纵截面AGBFig.5 Longitudinal section of the cube

图5中，S12是S1和S2连线的中点，也是S1和S2在纵截面的投影，OS12所在直线是正负序平面在纵截面的投影。线段AB=2，AG=2，OS12=/2，OB'=。

对于SPWM调制方式来说，在正常情况下，三相电网电压平衡且不发生过调制，其调制波矢量本身不含零序矢量，也就是调制波矢量与自身正负序矢量相等，即

满足式（32）的几何图形正是前文所述的截面正六边形S1～S6。当D位于图5所示的纵截面AGB时，D的分布范围仅限于OS12线段。根据式（31），当Dpn的模取最大值即OS12时，在相同的Vdc下可以得到最大幅值的Vs。即

当D位于所述纵截面之外的正方体内时，可以得到结论即D取得截面正六边形边上的点时，得到最大的Dpn和最高的电压利用率。由于O点到截面正六边形边上的所有点的距离不相等，到六边形顶点S1、S2、…、S6最长，到两相邻顶点中点如S12的距离最短，也就是瞬时的电压利用率是按六倍工频周期波动的。为了满足对不同相角的普适性，取最短距离OS12也就是截面正六边形内切圆半径作为计算恒定直流电压利用率的标准，则计算出直流电压利用率为

如果在 SPWM 的调制波矢量基础上允许添加零序矢量，同时保证调制波矢量位于空间正方体内，那么可以适当的零序矢量能使Dpn突破SPWM的限制，表达式为

如图5b所示，同样考虑D落在纵截面上，由于不再受D0=0的限制，D可以分布在AGB内任何一点（例如D1、D2、D3、D4均可）。过D作垂直于OS12、并与BA、BG相交所得的线段D0maxD0min，表示D0的允许范围。考虑D按D1、D2、D3、D4的顺序依次移动，D1的零序允许范围最大且符号包含正负；D2的零序允许范围减小，但是符号为非负；D3的零序允许范围进一步减小，但是Dpn已经突破了SPWM最大值的限制；最后D4的零序允许范围仅余一个点B，但是正负序矢量达到了最大值。所以，调制波矢量的零序矢量的适当添加，可以明显增大正负序矢量，从而提高电压利用率。

将D位于纵截面的结论推广到整个正方体内，则易得相应Dpn的取值范围扩展到了投影正六边形。与截面正六边形类似，投影正六边形的内切圆表示恒定直流电压情况下的Dpn的取值范围，则存在

对比式（34）和式（36）满足

式（37）表明，η2比η1的电压利用率高15.47%，反映了SVPWM电压利用率相对高的优点，也映证了本文的讨论。

综上，从几何角度解释，SPWM下的D被局限于正负序平面内，Dpn=D，所以Dpn被限制在最大半径为/2的圆内，从而限制了Vs的幅值及电压利用率；而SVPWM的D不局限在正负序平面，而是在正方体空间内，投影后得到的了Dpn的覆盖范围相对 SPWM 有明显扩大，从而达到了最大半径为的圆内，最大限度地提高了Vs的幅值。因此，调制波矢量的分布方式不同产生了所述两种调制方法。

3 利用调制波矢量构造SVPWM

3.1 调制波矢量的几何分布范围

其中满足

式（38）中γ(t)为t时刻的零序矢量的一个分量。Dpn取投影正六边形内切圆周，将圆周在垂直于∏pn的方向上下移动，形成轨迹的为圆柱面。正方体的与圆柱面相交的曲面与即为D的允许分布范围。对于每一个Dpn，以其矢量终点，垂直于∏pn作垂线，垂线与正方体的交线段便是允许零序的取值范围，超过了这个范围，就会出现过调制现象。如图 5b所示，与Dpn=D1，则零序分量的范围为[D0min,D0max]。

下面空间解析几何的角度分析各个区域内调制波矢量的特点。以图4的角F′OS1对应的扇形区域1为例，区域1内满足，圆柱面与x=1平面及z=-1平面相交。

根据几何定理，在所述区域内圆柱面与平面相交的轨迹曲线是空间椭圆。

平面x=1和圆柱面的联立方程为

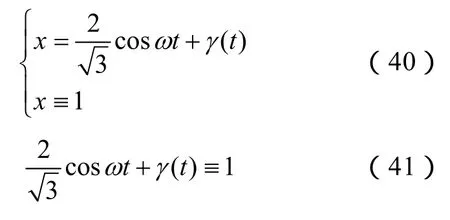
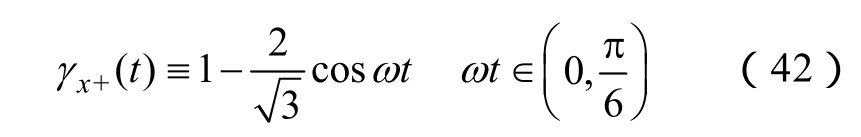
所以满足

平面z=-1和圆柱面的联立方程为

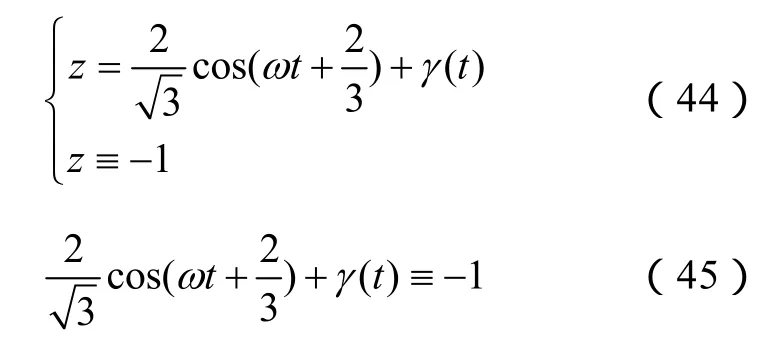
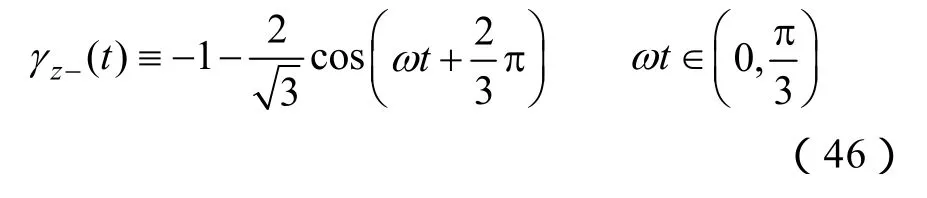
所以满足

对比式（43）和式（47）可得

所以，在区域1内，调制波矢量零序矢量的坐标取值为γx+(t)和γz-(t)组成的包络线区域内，并且所有取值均为负。

同理，可以得到圆柱面与正方体六个平面交线方程的零序矢量表达式。零序矢量在各个区域的分布范围如图6a所示，取零序上、下限的平均值绘制成空间曲面如图6b所示。

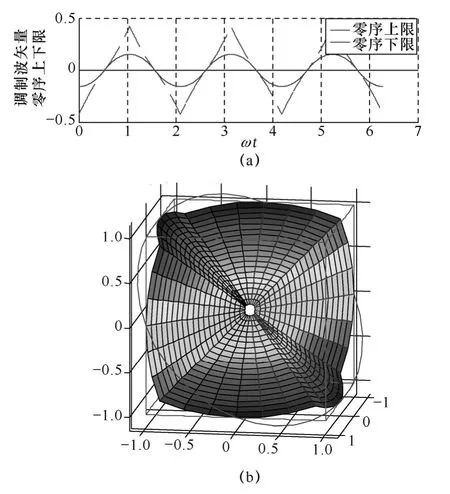
图6 调制波矢量的零序分量分布Fig.6 Zero sequence component of modulation wave vector

以上讨论了调制波矢量位于投影正六边形内切圆上的情况，调制波矢量位于内切圆内部时，分析方法类似，在此不作详细推导。图6a显示，零序矢量主体部分的分布呈3倍基波频率，因此可求得上、下限表达式。设定

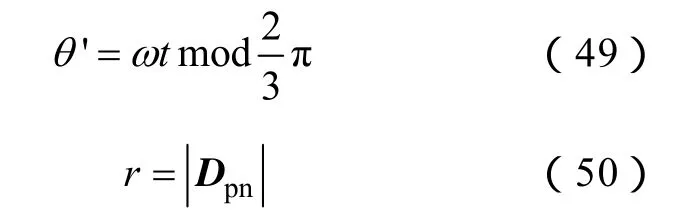
零序上限表达式

零序下限表达式

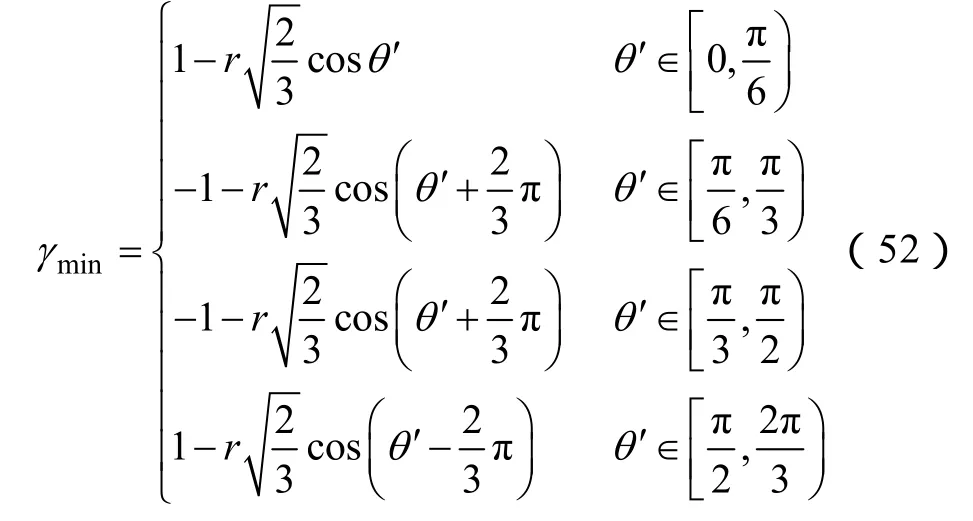
3.2 利用三维调制波矢量构造SVPWM

为了验证本文提出SVPWM构造法是否正确，以及超限是否为过调制，下面将以仿真和实验的形式分析，在含有不同零序矢量的SVPWM下的电压波形。本文采用零序上、下限加权叠加的方式来产生零序矢量：

将权值m和n不同组合产生的零序矢量注入三相平衡正弦波形来构造SVPWM。

4 仿真结果与分析

采用Matlab/Simulink进行仿真，仿真电路结构见图2，设定交流电压为零，直流电压为534V，负载Z为串联RC，其中R=10kΩ，C=2μF，载波频率为 3kHz。原始调制波为三相平衡正弦波，幅值为2/，根据m和n不同，添加零序矢量不同，分为以下5种情况：①m=0，n=0，SPWM过调制情况；②m=0，n=1。允许范围下限；③m=0.5，n=0.5，允许范围上下限中间值；④m=1，n=0，允许范围上限；⑤m=3，n=0，SVPWM过调制情况。

下面就这五种情况分别讨论，采样电压为RC端电压，仿真结果如图7所示。

图 7a～图 7e的 3个通道分别为三相调制波、调制波零序矢量、三相RC负载端电压。图7a～图7e为不同加权配置的对比，图7f是调制波A相与零序矢量的统一比较。下面对这五种情况分别分析。

图7 不同加权零序矢量情况下对比Fig.7 Comparison among different zero sequence component

图7a中，加权因子m=0，n=0，调制波矢量未添加零序矢量，调制波由于正弦峰值超过了1，处于SPWM过调制。从表中看出此时桥臂线电压THD达到5.53%，有效值有较小损失。

图7b、图7c和图7d中，加权因子m、n的作用使得零序矢量由本文给出的下限逐渐过渡到上限。全过程中，电压波形基本为正弦；桥臂电压THD较小；有效值几乎无损失。

图7e中，加权因子m=3，n=0，添加的零序矢量达到允许上限的3倍，处于SVPWM过调制。看到调制波在原正弦波峰谷处明显下陷，桥臂电压波形明显畸变，THD达到23.29%，有效值有较大损失。

从图7f可以看到图7a～图7e详细的渐变过程。

综上，Matlab仿真证明了利用调制波矢量构造SVPWM 方法是正确和有效的，能有效提高电压利用率，且给出的允许零序范围是正确的。

5 实验结果与分析

利用500kW逆变器并网实验平台，设定直流电压为 534V，经过串联 RC负载，其中C=2μF，R=10kΩ，载波频率为3kHz。原始调制波与仿真相同，幅值为2/。保持与仿真步骤一致，添加 5种的零序矢量，由加权因子m和n决定。图8表示三相RC负载端电压波形。

图8 不同零序矢量的实验结果比较Fig.8 Comparison among different zero sequence component in expriments

图8a表示m=0,n=0情况下B相负载端电压实际波形，波形含有开关频率次谐波。为了观察和分析低于开关频率的电压波形，用示波器自带的低通滤波（截止频率500Hz）进行滤波后得到图8b，其他情况下均进行相同滤波得到图8c～图8f。

图 8b、图 8f表明调制波矢量添加的零序超出允许范围即发生过调制时，桥臂电压有明显畸变，图8c、图8d、图8e表明调制波矢量添加零序在允许范围内时，桥臂电压波形正确，且波形几乎完全一致。实验结果与仿真一致，表明调制波矢量的研究与SVPWM的构造方法是正确有效的。

6 结论

本文基于空间直角坐标系，提出了三维空间调制波矢量的概念和研究方法。新方法将三相物理量进行三维矢量化，得到了简洁有效的表达式，并在空间中以图形化的方式表达了矢量，具有明确的几何含义，分析和计算非常直观，可以方便地使用空间解析几何理论以及矢量理论作为数学工具进行分析研究。

从调制波矢量的角度得到了SPWM和SVPWM解析表达式，使调制方法与控制策略及主电路成为一个整体，便于统一建模。

给出调制波矢量允许零序矢量的范围。对零序矢量范围上、下限进行加权叠加产生合适的调制波零序矢量，从而构造 SVPWM，实现过程简单，且不会发生过调制。若发生了过调制，利用本文给出的调制波矢量零序范围，可以精确计算出过调制的程度，研究过调制的抑制或补偿。

关于过调制的抑制或补偿控制，以及如何基于矢量化的控制策略、调制方法和主电路的建模提出更优的方法，以后将有进一步的研究。

[1] 王晶晶, 徐国卿, 王麾. 基于DSP的两种SVPWM技术实现方案研究[J]. 电工技术杂志, 2003, 22(1): 39-42.

Wang Jingjing, Xu Guoqing, Wang Hui. Study and realization of two different SVPWM technique with DSP[J]. Electrotechnical Journal, 2003, 22(1): 39-42.

[2] 刘家军, 姚李孝, 吴添森, 等. PSCAD/EMTDC中SVPWM 算法的实现[J]. 电力系统保护与控制,2010, 38(18): 120-125.

Liu JiaJun, Yao Lixiao, Wu Tiansen, et al. Implementation of SVPWM algorithm in PSCAD/EMTDC[J]. Power System Protection and Control, 2010,38(18): 120-125.

[3] Lai Y S, Bowes S R. Optimal bus-clamped PWM techniques for three-phase motor drives[C]. IECON 2004, Busan, 2004, 2: 1475-1480.

[4] 徐蕴婕, 邱阿瑞, 袁新枚, 等. 舰船交流电力推进系统 PWM 方式的比较[J]. 电工技术学报, 2006,21(2): 93-96．

Xu Yunjie, Qiu Arui, Yuan Xinmei, et al. A comparison of SVPWM and SPWM in AC ship power propulsion systems[J]. Transactions of China Electrotechnical Society, 2006, 21(2): 93-96.

[5] 熊健, 康勇, 张凯, 等. 电压空间矢量调制与常规SPWM 的比较研究[J]. 电力电子技术, 1999, 1(1):25-28.

Xiong Jian, Kang Yong, Zhang Kai, et al. Comparison study of voltage space vector PWM and conventional SPWM[J]. Power Electronics, 1999, 1(1): 25-28.

[6] 程启明, 程尹曼, 薛阳, 等. 三相电压源型PWM整流器控制方法的发展综述[J]. 电力系统保护与控制,2012, 40(3): 145-155.

Cheng Qiming, Cheng Yinman, Xue Yang, et al. A summary of current control methods for three-phase voltage-source PWM rectifiers[J]. Power System Protection and Control, 2012, 40(3): 145-155.

[7] 于飞, 张晓锋, 乔鸣忠. 基于零序信号注入的载波型多相 PWM 控制技术[J]. 电工技术学报, 2009,24(2): 127-131.

Yu Fei, Zhang Xiaofeng, Qiao Mingzhong. Multiphase carrier PWM control technology based on zerosequence signal injection[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 127-131.

[8] 周卫平, 吴正国, 唐劲松, 等. SVPWM的等效算法及SVPWM与SPWM的本质联系[J]. 中国电机工程学报, 2006, 26(2): 133-137.

Zhou Weiping, Wu Zhengguo, Tang Jinsong, et al. A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM[J].Proceedings of the CSEE, 2006, 26(2): 133-137.

[9] 文小玲, 尹项根, 张哲. 三相逆变器统一空间矢量PWM实现方法[J]. 电工技术学报, 2009, 24(10): 87-93.

Wen Xiaoling, Yin Xianggen, Zhang Zhe. Unified space vector PWM implementation method for threephase inverters[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 87-93.

[10] 李涛, 张晓锋, 乔鸣忠. SPWM与SVPWM的宏观对等性研究[J]. 中国电机工程学报, 2010, 12(30):178-184.

Li Tao, Zhang Xiaofeng, Qiao Mingzhong. Research on the macro-equivalence between SPWM and SVPWM[J]. Proceedings of the CSEE, 2010, 12(30): 178-184.

[11] 陆海峰, 瞿文龙, 张磊, 等. 基于调制函数的SVPWM算法[J]. 电工技术学报, 2008, 23(2): 37-43.

Lu Haifeng, Qu Wenlong, Zhang Lei, et al. SVPWM algorithm based on modulation functions[J]. Transactions of China Electrotechnical Society, 2008, 23(2):37-43.

[12] Van der Broeck H W, Skudelny H C, Stanke G V.Analysis and ealization of a pulsewidth modulatorbased on voltage space vectors[J]. IEEE Transactions on Industry Applications, 1988, 24(1): 142-150.

[13] Hava A M, Kerkman R J, Lipo T A. Simple analytical and graphical methods for carrier-based PWM-VSI drives[J]. IEEE Transactions on Power Electronics,1999, 14(1): 49-61.

[14] Implementation of a Speed Field Orientated Control of Three Phase AC Induction Motor using TMS320F240(BPRA076)[M]. Texas Instruments: TI Inc, 1998.

[15] 邱银锋, 梁志珊. abc坐标系下空间矢量PWM实现研究[J]. 电力系统保护与控制, 2011, 39(13): 36-40.

Qiu Yinfeng, Liang Zhishan. Research on implementation of the space vector PWM in abc coordinates[J].Power System Protection and Control, 2011, 39(13):36-40.

[16] Sun Qiang, Yin Zhonggang, Zhong Yanru. A dual single-input single-output model of PWM rectifier based on α-β stationary frame[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 73-79.

[17] 吴玉杨. 基于三维空间矢量调制的三相四桥臂逆变器研究[D]. 合肥: 合肥工业大学. 2007.

[18] 王晓刚, 谢运祥, 帅定新, 等. 四桥臂逆变器的快速三维 SVPWM 算法[J]. 华南理工大学学报(自然科学版), 2009, 37(7): 94-99.

Wang Xiaogang, Xie Yunxiang, Shuai Dingxin, et al.Fast three-dimension SVPWM algorithm for four-leg inverter[J]. Journal of South China University of Technology, 2009, 37(7): 94-99.

[19] 周娟, 吴漩, 蒋正友, 等. 四桥臂变流器新型三维空间矢量脉宽调制策略[J]. 中国电机工程学报,2011, 31(33): 1-8.

Zhou Juan, Wu Xuan, Jiang Zhengyou, et al. A novel 3D-SVPWM algorithm for four-leg converter[J].Proceedings of the CSEE, 2011, 31(33): 1-8.