基于优化虚拟矢量的三电平逆变器中点电位平衡闭环控制

范 波 赵伟刚 刘 刚 谢冬冬

（1. 河南科技大学电子信息工程学院 洛阳 471023 2. 中信重工机械股份有限公司 洛阳 471039）

1 引言

目前，多电平逆变器由于在电力转换方面具有诸多优点，逐渐成为一个特别活跃的研究方向[1-5]。相较两电平而言，多电平逆变器主电路开关管承受的电压应力、输出电压的谐波失真和转换损耗均有所降低。然而由于大量开关器件的应用，使其控制策略变得更复杂。

在多电平逆变器的诸多拓扑结构中，二极管中点钳位型（Neutral Point Clamped，NPC）三电平逆变器由于结构简单、输出波形质量高，得到了国内外学者的青睐[6-11]。但其存在直流侧电容电压的低频振荡，进而会增加开关管承受的电压应力，并会在输出电压中包含低频谐波。国内外学者针对这些问题做了许多研究工作。文献[12]提出一种预测控制策略来控制 NPC三电平逆变器直流侧电容电压的平衡。然而，该控制方法需要关于负载模型的先验知识。文献[13]提出利用最近三虚拟空间矢量（NTV2），能在输出电压的全局范围内有效控制中点电压平衡。文献[14]提出一种类似的 NTV2PWM控制方案实现对NPC逆变器的控制。文献[15]提出利用优化最近三虚拟空间矢量（ONTV2）来控制中点电位平衡。然而上述虚拟空间矢量（VSVPWM）算法，无法处理计算中近似处理与累积效应造成的中点电位不平衡。文献[16]提出利用 SVPWM 与VSVPWM 混合调制的方式。该方案虽然可有效弥补 VSVPWM控制方式的不足，但实现时必须分别根据两者的约束条件得到切换条件，使算法复杂化，并且 NPC逆变器仍会在输出电压中产生低频谐波失真。

本文提出一种基于ONTV2PWM的闭环控制方式，该调制方式是建立在dqo坐标系下，利用一种特定的方式——根据中点电压的反馈量来循环改变控制器的调制波形，对中点电压平衡进行快速控制；控制方案剩下的部分类似于两电平，通过恰当的方式与已选定的调制算法相衔接。另外，增加了对负载位移角的在线估计环节。仿真及实验验证了该控制方式的可行性。

2 优化虚拟空间矢量脉宽调制

首先定义dap、dbp、dcp、dan、dbn、dcn为 a-b-c坐标系下6个独立的相占空比，dpd、dpq、dpo、dnd、dnq、dno为d-q-o坐标系下6个独立的控制变量，其中dxy代表x相连接到直流侧y点时的占空比。两个坐标系下独立控制变量之间的转换关系

其中

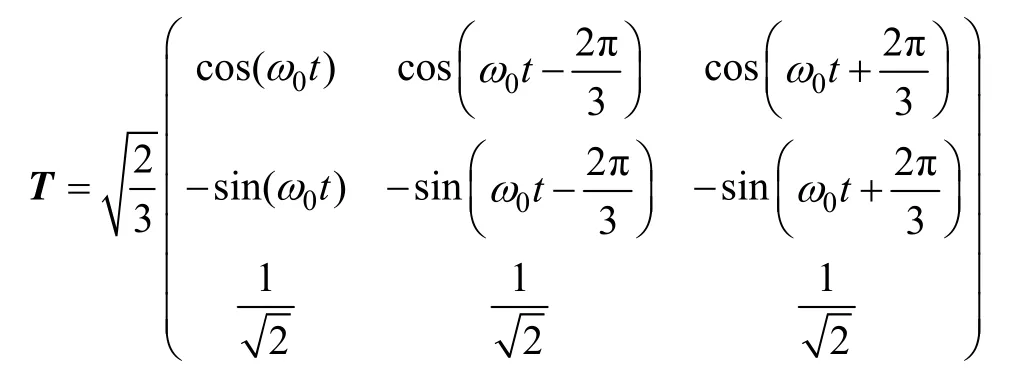
图1为ONTV2PWM调制算法下第一扇区空间矢量图，其中VG0、VGSi、VGMi、VGLi（i=1, 2,…, 6）是由基本空间矢量经过线性组合得到，线性组合的系数用r1～r7来表示。在每个开关周期内，参考电压矢量Vref=meiθ（m∈[0, 1],θ=ω0t）由最近的 3 个虚拟空间矢量来合成。在此，需要对线性组合的系数进行优化处理。

图1 虚拟空间矢量图Fig.1 Virtual space vector diagram

定义在nfs附近的输出电压的谐波失真为

式中，Vh为输出端线电压的h次谐波的方均根。为了能保证在每个开关周期时间内中性点的平均电流值io=0，关键是如何选择r1,k～r7,k的值来保证Vdis,1取得最小值。由于对称性，仅需求出第一扇区的r1,k～r7,k的值即可。类似于文献[17]所介绍的方法，为了能得到最小化的Vdis,1，那么在第一扇区内，则需要在每个开关周期内，k次谐波指标HD1,k为最小。因此，对于给定的调制度m和负载转矩角φ，此优化问题可用式（3）来进行论证。

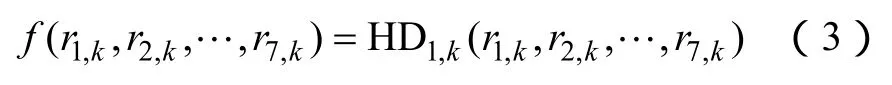
其中

通过上面的分析，利用式（4）来定义在d-q-o坐标系下，基于以上6个独立占空比的ONTV2PWM。

此处，m(∈[0, 1])和θ分别为参考电压矢量Vref的长度和角度，变量φ为负载位移角；参数K为m和φ的函数，即

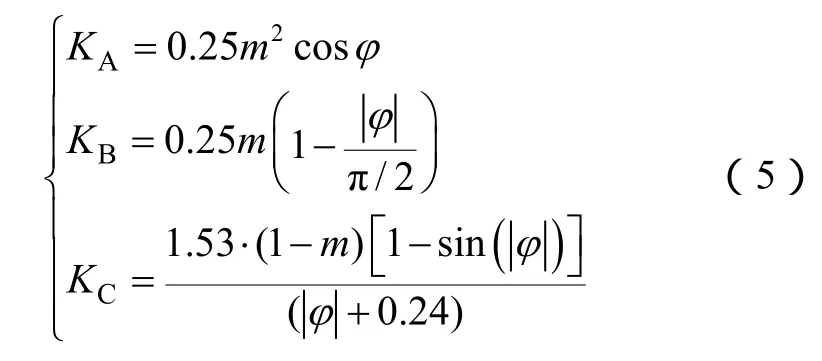
m-φ组成的区域被划分为A、B、C 3个区域，如图2所示，其中3个区域的分界线mbAB、mbBC由式（6）来表示。

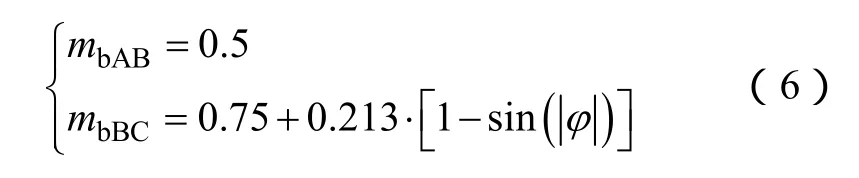
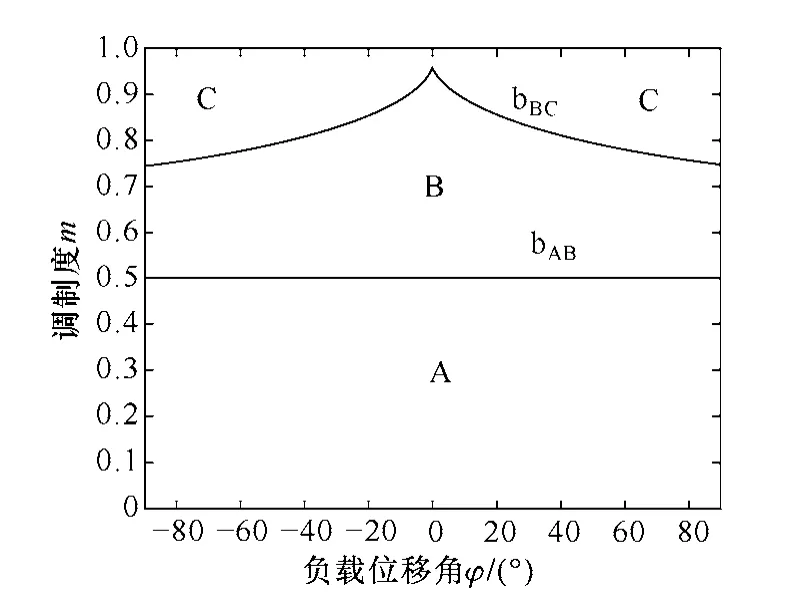
图2 负载位移角与调制指数的关系图Fig.2 Load displacement angle and modulation index relationship diagram

给定了m、θ和tanφ的值，由式（4）和式（5）可得到在dqo坐标下的占空比dap、dbp、dcp、dan、dbn、dcn。例如，在第一扇区，dap=dpoo+dpnn+ dppn+dpon+dppo，根据这些独立的占空比，在一个开关周期内，假设产生的序列是按照对称性p-o-o-p形式来控制每相如何连接直流侧端点，这样就会非常简单地产生12路开关控制信号。

3 闭环控制方案设计

本文提出的闭环控制方案如图3所示，主要有NPC三电平逆变器（见图3a）、控制器（见图3b）和调制器及调制波分配器（见图3c）组成。该闭环控制方案同样可应用于更高电平的逆变器系统。

3.1 直流侧中点电压平衡控制

NPC三电平逆变器的直流侧中点电位不平衡（或偏移），是指直流母线端的两个相互串联连接电容充放电时，由于充放电电流不平衡等各种原因，使得与其相连的中点电位发生波动或偏移的问题。它是该拓扑结构固有的一种现象，在变频器输出多电平工作时，电路输出的零电平是由二极管钳位到直流母线的中点得到的，随着电力电子开关状态的转换，电流伴随着电容的充电或放电，会流出或流入直流母线的中点，这样就可能造成中点电位发生偏移或不平衡。

（a）NPC三电平逆变器拓扑结构及控制方案

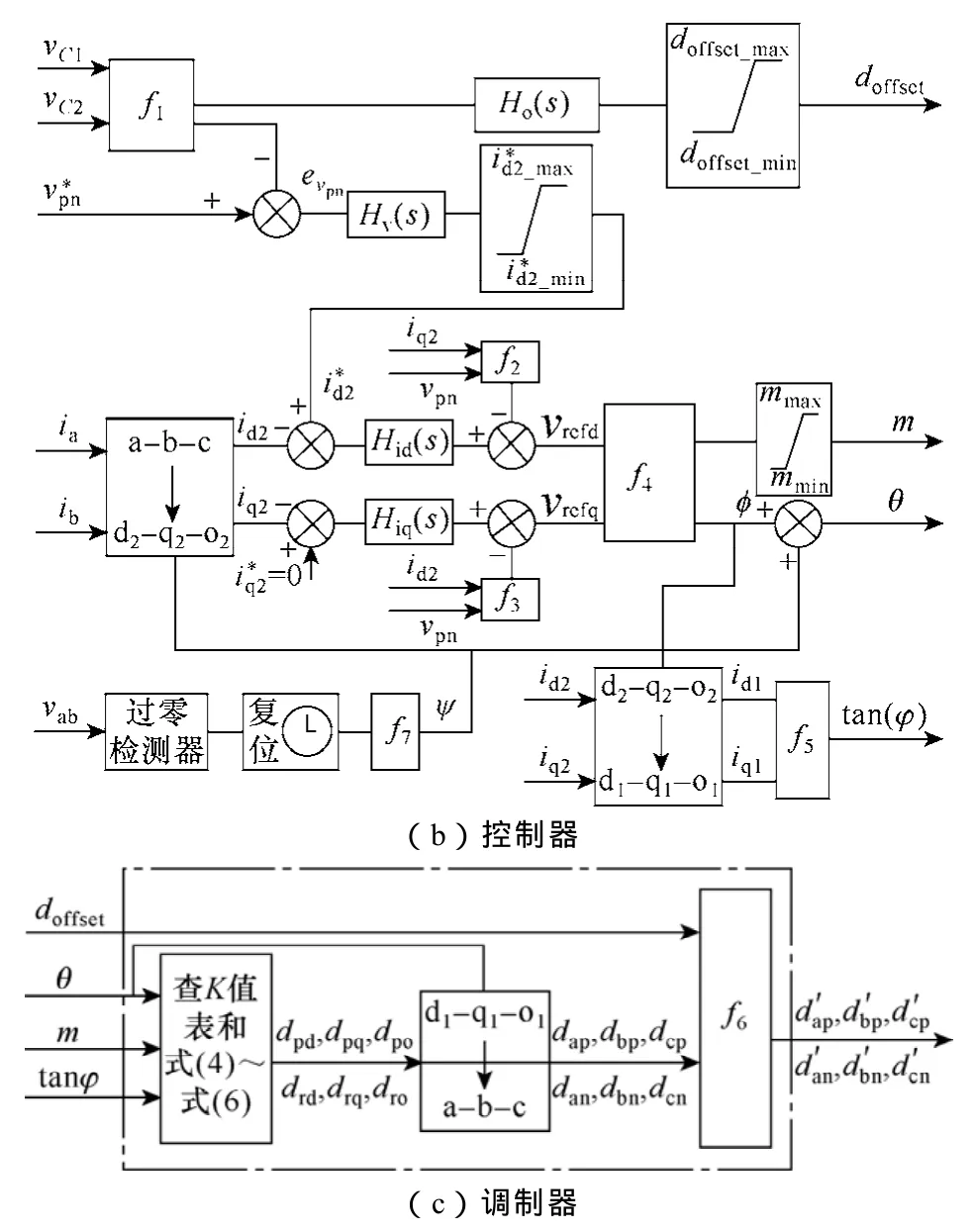
图3 闭环控制方案图Fig.3 The closed-loop control scheme block diagram

本文所提及的控制方案适用于 ONTV2PWM，将根据逆变系统的负载情况，保证不会产生类似于vunb=(vC1-vC2)/2的低频振荡。如果设置k=0，由式（1）可知：无论负载表现出多么严重的非线性和不平衡性，ONTV2PWM 对直流侧中点电压平衡调节均无影响，如图4a所示；若k＞0，ONTV2PWM可以使中点电位很自然地恢复到平衡，如图4b所示，且k值越大，调节速度越快，否则，响应速度会很慢。

图4 ONTV2PWM方案下电容电压波形Fig.4 The capacitive voltage waveform under ONTV2PWM

根据先验知识可知，引入共模电压模型后，哪个调制波形需要被修改变得不再明显，因此，每相中均引入两个调制波形（dxp和dxp）。在dap-dan，dbp-dbn，dcp-dcn的调制波形中分别增加一个补偿量。对增加的补偿量有3种设置：①在dxp上增加补偿量；②在dxp上减少补偿量；③在dxp上增加补偿量的一部分，同时在dxp上减去补偿量剩下的部分。

通过一个简单的策略来简化补偿量如何应用于占空比。考虑到占空比必须大于零，如果一个占空比接近于零，那与之对应的占空比将增加一个与之相匹配的补偿量。该控制策略可增加非零占空比趋近于零出现的次数，因此，可减少换向的次数。针对参考空间矢量，按照该策略，x相占空比可由如下规则表示

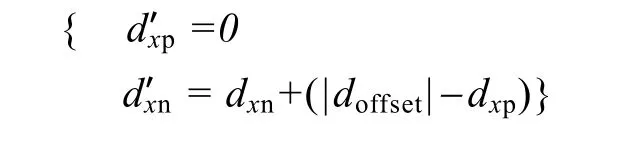
补偿量doffset的值，是由基于直流侧电容电压不平衡量vunb=(vC1-vC2)/2的补偿器决定的。在采样频率低于开关频率时，为了仅修正影响直流侧电容电压平衡的扰动，此补偿器必须具有低通特性。如果直流侧中点的功率流向发生变化，那么补偿量doffset也要随之发生变化。在实际应用中，功率流向是时刻变化的，因此，需要对该变量进行实时检测，以便及时采取一个合适的控制措施。

相比较文献[14]的控制方案，此处提出的方案具有以下优点：

（1）该方案适用于ONTV2PWM控制方案下所有的K值。

（2）具有非常有效地维持平衡性的措施，对于任意给定的开关周期，能同时恢复被干扰的a、b、c三相的平衡性，取代了之前仅能恢复单相的平衡性，并且所采取的维持平衡性的措施并未对所涉及的相占空比的最小值进行限制。

（3）具有较低次数的开关转换，因此，首次利用占空比得到补偿量的过程将被简化，它将最大化由非零占空比趋近零值的机会，进而减少开关转换次数。

（4）在单向功率传输应用中，不需要对相电流进行采样处理。

3.2 参考矢量的计算

从闭环控制的观点出发，两电平与三电平最大的不同点是后者引入了直流侧中点电压的动态。由于选择的调制方法及预先提出的针对中点电位平衡的控制方案，假设直流侧中点电压一直是平衡状态，那么三电平逆变器就类似于两电平逆变器，因此，针对两电平的传统控制方案和程序就可以直接应用到三电平上，来获得调制器设计中需要的参考矢量的长度m和角度θ。

针对本文选择的控制方案，首先，直流侧电压vpn=vC1-vC2，该值将与期望值相比较，所产生的误差evpn经过一个补偿器的处理后，产生id的期望值。由于ic=ia-ib，因此无需检测ic值。首先要进行a-b-c到 d2-q2-o2的坐标变换，d2轴与相对于中性点的线电压矢量VL-N所在的相重合。如图5所示，该矢量与α轴之间存在一个夹角ψ，其中

图5 参考矢量Vref与VL-N的位置关系图Fig.5 Location of vectorsVrefandVL-Nthat is withreference to the axis α

电流分量id2和iq2分别与它们对应的期望值作比较，在保证功率转换不变的前提下，为了获得一个与之相匹配的位移角，设定iq2的期望值为零。d轴和q轴上分量的误差分别要经过专用补偿器的处理。最后，对所有的分量进行解耦处理，得到的结果是参考空间矢量Vref在d2与q2上的分量。通过式（5）可得到参考矢量Vref的长度m（调制指数）和相对于d2轴的夹角φ。

另外，在调制过程中，从d1-q1-o1到a-b-c的坐标变换中，所需的角度θ可通过式（9）得到。

3.3 负载位移角的在线估计

为了实施 ONTV2PWM 控制方案，需要对 tanφ进行估值。角度φ对应于基本线电流矢量与Vref的夹角，因此，可简单地通过传感器测量线电流，利用坐标变换以及x相占空比规则，便可计算出tanφ的值。

负载位移角的计算仅需通过传感器对线电流进行采样，ONTV2PWM 调制方法的实施不再需要额外的传感器。

4 仿真与实验及结果分析

利用Matlab/Simulink软件对本文所提的控制方案进行仿真分析，验证方案的可行性，仿真结果如图6所示，可观察到：当直流侧给定电压从 720V降到 400V时，在一个短暂的时间内，直流侧电容电压很快恢复到新的平衡。考虑到ONTV2PWM调制方案已基本上可保证直流侧电容电压的平衡，所以控制器中的补偿量的范围较小（-0.001＜doffset＜0.001）。

图6 直流侧电容电压仿真波形Fig.6 DC side capacitive voltage simulation waveform diagram

实验平台结构如图7所示，主电路功率模块采用 IGBT，控制器模块及调制模块使用 TI公司的TMS320S2812，负载为交流笼型异步电机，其型号Y112M-4B，参数为PN=4kW，UN=380V，IN=8.8A，p=2，R=1 440r/min；另外，考虑到负载对直流侧分压电容的影响，即在一定的阈值范围内，直流侧电容中点电位波动随负载转矩增大而增大，然而在实际工程应用中，由于电压等级高，负载对其影响可忽略不计。在此，仅对异步电动机进行空载试验；另外，开关频率fs=1 0kHz ，中间直流侧电压600V，直流侧上、下电容值均为840μF，驱动电路采用PSHI2012驱动板。

图7 NPC三电平逆变器系统框图Fig.7 NPC three-level inverter system diagrams

实验结果如图8所示，可看出：在对中点电位未加控制时（见图8d），其波动幅值范围在±10V内，而在闭环控制条件下（见图8e），波动幅值范围在±1 V 内，显而易见，对中点电位平衡施加闭环控制方式后，直流侧中点电位的波动幅值得到显著减小。文献[13-15]提出VSVPWM控制方式下，直流侧中点电位虽得到了有效控制，但逆变器输出的相电压在一个采样周期内出现了2次开关动作，增加了器件的开关损耗，并使输出电流波形发生了畸变；文献[16]提出 VSVPWM和 SVPWM混合调制方式下，虽达到了有效控制中点电位平衡的目标，但逆变器输出的相电压明显在很少的采样周期内仍出现了 2次开关动作，未完全弥补 VSVPWM方式的不足。相比较以上滞环控制方式，本文提出的闭环控制方式，不仅可满足对中点电位平衡的有效控制，且NPC三电平逆变器输出的线电压、相电压及电流波形也更趋近于正弦波，谐波含量减少，减小了系统的EMI，这样有利于得到更良好的系统性能，验证了闭环控制方式的正确性和有效性。

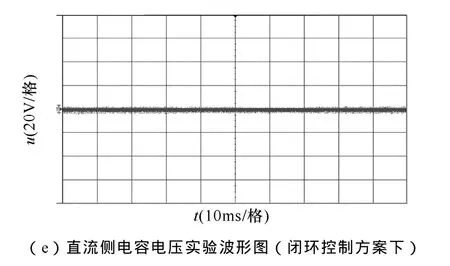
图8 实验结果波形Fig.8 The experimental result waveforms

5 结论

针对 NPC三电平逆变器的中点电位不平衡所引起的直流侧电容电压振荡、功率器件电压应力增加和输出电压谐波等问题，本文提出了一种基于ONTV2PWM 的闭环控制方案。利用一种特定的方式——根据中点电压的反馈量来循环改变控制器的调制波形，对中点电压平衡进行快速控制；控制方案剩下的部分类似于两电平，通过恰当的方式与已选定的调制算法相衔接，同时增加了对负载位移角的在线估计环节，有效提高了对中点平衡的控制性能，减小了直流侧电容波动。本文提出的闭环控制方案可扩展应用于多电平逆变系统中，对提高大功率、高压变频调速系统控制性能有一定实际意义。

[1] 李永东, 肖曦, 高跃. 大容量多电平变换器—原理·控制应用[M]. 北京: 科学出版社, 2005.

[2] Franquelo L G, Prats M A M, Portillo R C, et al.Three dimensional space-vector modulation algorithm for four-leg multilevel converters using abc coordinates[J]. IEEE Transactions on Industrial Electronics,2006, 53(2): 458-466.

[3] 赵辉, 李瑞, 王红君, 等. 60°坐标系下三电平逆变器 SVPWM 方法的研究[J]. 中国电机工程学报.2008, 28(24): 39-45.

Zhao Hui, Li Rui, Wang Hongjun, et al. Study on SVPWM method based on 60°coordinate system for three-level inverter[J]. Proceedings of the CSEE, 2008,28(24): 39-45.

[4] Lewicki A, Krzeminski Z, Abu-Rub H. Space-vector pulsewidth modulation for three-level NPC converter with the neutrai point voltage control[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5076-5086.

[5] Gupta K, Khambadkone A M. A space vector PWM scheme for multilevel inverters based on two-level space vector PWM[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1631-1639.

[6] Nabae A, Takahashi I, Akaja H. A new neutral pointclamped PWM inverter[J]. IEEE Transactions on Industry Application, 1981, 17(5): 518-523.

[7] 姜卫东, 王群京, 史晓锋, 等. 中点钳位型三电平逆变器在空间矢量调制时中点电位的低频振荡[J].中国电机工程学报, 2009, 29(3): 49-55.

Jiang Weidong, Wang Qunjing, Shi Xiaofeng, et al.Low frequency oscillation of neutral point voltage of neutral-point-clamped three-level VSI under SVPWM control[J]. Proceedings of the CSEE, 2009, 29(3):49-55.

[8] Maheswari Ramkrishan, Munk-Nielsen S, Busquets-Monge S. Design of neutral-point voltage controller of a three-level NPC inverter with small Dc-link capacitors [J]. IEEE Transactions on Industrial Electronics,2013, 60(5): 1861-1871.

[9] Yazdani A, Iravani R. A new neutral point-clamped PWM inverter[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 414-424.

[10] 宋文祥, 陈国呈, 陈陈. 基于矢量合成的三电平空间电压矢量调制方法[J]. 电工技术学报, 2007,22(10): 91-96.

Song Wenxiang, Chen Guocheng, Chen Chen. A space vector modulation method of three-level NPC inverter based on synthesizing vectors concept[J].Transactions of China Electrotechnical Society, 2007,22(10): 91-96.

[11] Pou J, Zaragoza J, Ceballos S, et al. A carrier-based PWM strategy with zero-sequence voltage injection for a three-level neutral-point clamped converter[J].IEEE Transactions on Power Electronics, 2012, 27(2):642-651.

[12] Vargas R, Cortes P, Ammann U, et al. Predictive control of a three-phase neutral-point-clamped inverter[J]. IEEE Transactions on Industrial Electronics, 2007,54(5): 2697-2705.

[13] Busquets-Monge S, Bordonau J, Boroyevich D, et al.The nearest three virtual space vector PWM-A modula-tion for the comprehensive neutral-point balancing in the three-level NPC inverter[J]. IEEE Power Electron.Lett. , 2004, 2(1): 11-15.

[14] Pou J, Zaragoza J, Rodriguez P, et al. Fast-processing modulation strategy for the neutral point-clamped converter with total elimination of low-frequency voltage oscillations in the neutral point[J]. IEEE Transactions on Industrial Electronics, 2007, 54(4):2276-2287.

[15] Busquets-Monge S, Somavilla S, Bordonau J, et al.Capacitor voltage balance for the neutral-point-clamped converter using the virtual space vector concept with optimized spectral performance[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1128-1135.

[16] 姜卫东, 杜少武, 史晓峰, 等. 中点箝位型三电平逆变器空间矢量与虚拟空间矢量的混合调制方法[J]. 中国电机工程学报, 2009, 29(18): 47-53.

Jiang Weidong, Du Shaowu, Shi Xiaofeng, et al.Hybrid PWM strategy of SVPWM and VSVPWM for neutral point-clamped three-level voltage source inverter[J]. Proceedings of the CSEE, 2009, 29(18):47-53.

[17] Busquets-Monge S, Bordonau J, Boroyevich D, et al.Output voltage distortion characterization in multilevel PWM converters[J]. IEEE Power Electronics Letters,2004, 2(1): 24-28.