基于新型四象限开关单元的并联型有源滤波器

陈 仲 王志辉 陈 淼

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

有源电力滤波器（Active Power Filter，APF）因其突出的优点得到了广泛的研究，在有源滤波器的拓扑结构[1-3]、谐波检测[4,5]和控制策略[6-8]等方面取得了大量的研究成果和应用。已有的有源滤波器几乎均采用电压源型桥式变换电路，其存在的桥臂直通隐患，难以满足某些场合，如航空航天领域、敏感性负载等对可靠性的高要求。为了避免直通往往在驱动信号中加入死区时间，但是由于引入非线性因素而必然导致有源滤波器补偿性能的下降；两者互相制约，往往不可兼得，而通过控制上的调整来抑制死区带来的负面效应则显得比较复杂[9,10]。

交错降压式电路（Interleaved Buck, IB）是近年来出现并得到研究的一种新型变流拓扑，其实质上是一种基于 DC-DC电路并联构成的组合变换器[11-14]。鉴于其呈现出很多独到的特性，特别是高可靠性和优异性能，将该逆变技术运用于有源电力滤波器中，具有一定的理论意义和实用价值。

本文在分析交错降压原型电路的基础上，给出一种半桥交错降压式有源电力滤波器（Interleaved Buck-Active Power Filter，IB-APF）。详细介绍其工作原理和控制策略，并设计了一台 2kV·A、28kHz的原理样机，通过仿真和实验验证该新型有源滤波器的可行性。进而通过对常用三端口网络的分析和组合，研究交错降压开关单元的生成规律；基于交错降压开关单元，提出一族新颖的并联型有源电力滤波器拓扑。

2 半桥交错降压并联型APF

2.1 交错降压电路

Gerald R. Stanley等人提出一种用单管桥臂替代双管桥臂结构的 DC-AC变流器[12]，它包含两个桥臂和两个滤波电感，主电路拓扑及其工作波形如图1a和图1b所示，其中，桥臂结构为功率管和二极管串联形式，有效杜绝了桥臂直通的危险，极大提高了电路的可靠性；且可以分别优化设计对应的功率管和二极管，进一步提高变换效率和性能。

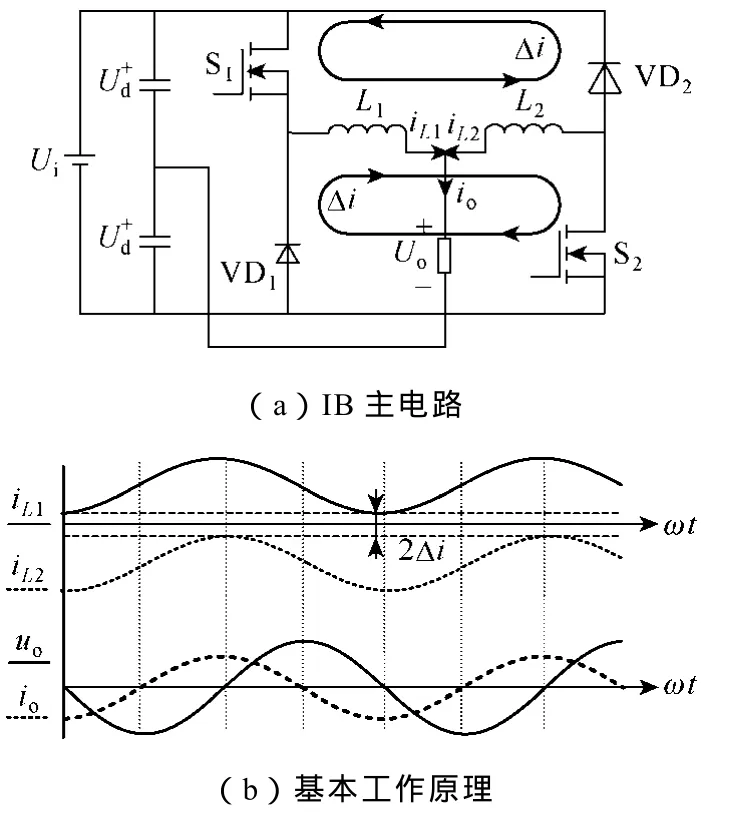
图1 IB电路结构和基本工作原理Fig.1 Topology and operation principle of interleaved buck circuit

在理想条件下，该逆变器输出标准正弦电压和电流，电感电流iL1、iL2为临界连续的正弦电流，两者与输出电流保持同频同相位。但是，当轻载条件时，电感储能能力有限，输出电流断续会导致输出电压出现畸变。因此，在导通电感中增加一定的偏置电流 Δi以保证电感电流iL1、iL2始终连续。但是由于偏置电流 Δi作为环流始终存在却不参与电能传输，因此大大降低了变换器效率。

由于该变流器在传输和回馈电能阶段均可看成是 Buck电路的工作性质，因此可被称为交错降压式电路（Interleaved-Buck，IB）。基于对IB电路的分析，本文提出一种半桥结构的新型APF，本文称之为半桥交错降压式APF（以下简称半桥IB-APF），继承了IB电路内在具有的优势。

2.2 半桥交错降压式有源滤波器

图2所示为半桥 IB-APF的系统框图，其中半桥IB-APF根据IB拓扑结构对传统半桥APF的双管桥臂进行改进，采用开关管和二极管反相串联桥臂结构（VD1和Q1串联，Q2和VD2串联），直流侧采用分裂电容（C1和C2）结构，两个桥臂中点E、F之间的串联电感（L1和L2）中点 M和直流侧分裂电容连接中点N作为APF的交流输出接入电网PCC点。

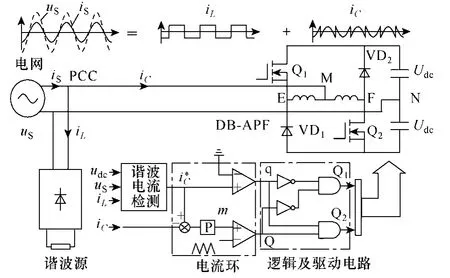
图2 半桥IB-APF系统框图Fig.2 System diagram of half bridge IB-APF

只需要采样电网电压、负载电流，根据谐波及无功算法获取补偿电流基准，并维持直流侧电容电压的均衡与稳定，利用电流环和逻辑及驱动电路控制半桥 IB-APF即可完成对非线性负载的谐波抑制和无功补偿目的。

3 IB-APF控制方法

3.1 工作原理

半桥 IB-APF补偿系统谐波时的工作原理和模态分别对应图3和表1中所示1、2、3、4四个过程。

图3 半桥IB-APF工作原理Fig.3 Equivalent operation stage of half bridge IB-APF

为了提高APF的效率，采用一种新的电流控制方法以消除电感环流，其基本思想为：在开关管Q1、二极管 VD1和电感L1以及开关管 Q2、二极管 VD2和电感L2组成的两路并联Buck变换器中，前者传输负向补偿电流iC1，后者传输正向补偿电流iC2，两路Buck电路的输出电流叠加即为APF的总补偿电流iC。因此，电感电流是断续的波形，且始终为单一极性。

表1 半桥IB-APF工作模态Tab.1 Working model of half bridge IB-APF

3.2 调制方法

滞环电流控制硬件电路实现简单，属于实时控制，电流瞬态响应快；输出电流的畸变始终保持在一个给定容差范围内，峰值电流受到限制；电网电压波动对控制影响不大，稳定性较好等。但是其开关频率不固定，会随补偿电流变化而波动，开关纹波不易滤除，带来并不期望的谐波流入电网，产生噪声的问题；而且，大功率情况时，开关频率不固定容易导致开关管失控。更重要的是，虽然电流脉宽不等固然可以维持电感端压的伏秒平衡，但是会导致电容电荷的安秒不平衡，在半桥电路结构中，这种不平衡会导致直流侧分裂电容电压的不均衡，恶性循环的结果将使APF失控。因此，下文主要研究分析 IB-APF的三角波比较电流控制方法。

图4所示为半桥IB-APF的SPWM控制原理。当调制波m与三角载波调制时，产生高频双极性控制信号Q，结合调制信号的低频极性判断信号q，可以得到开关管Q1、Q2的驱动信号。

APF的两个桥臂中点电压uEN、uFN也具有一定特点：补偿电流iC＞0时，Q2高频开关，uFN为±Udc，Q1所在桥臂和电感L1不参与功率传输，uEN跟随电网电压uS变化；反之，补偿电流iC＜0时，Q1高频开关，uEN为±Udc，Q2所在桥臂和电感L2不参与功率传输，uFN跟随电网电压uS变化。任何阶段，参与工作的桥臂中点输出电压均为±Udc两电平，所有功率器件承受的反向压降为2Udc。

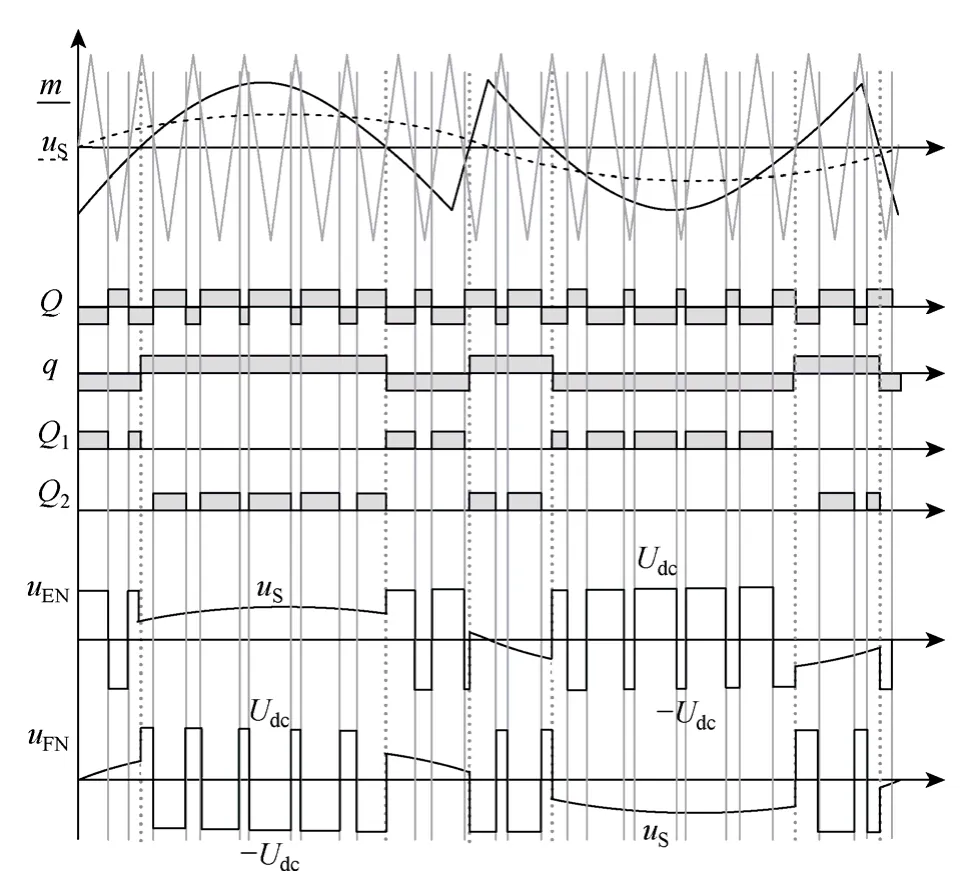
图4 半桥IB-APF SPWM控制原理Fig.4 SPWM modulation strategy of half bridge IB-APF

结合其硬件实现方式，如图2中所示逻辑及驱动电路，电流环输出调制信号与三角载波进行调制可得图4所示的控制信号Q，基准经过过零比较器得到图 4所示的低频极性判断信号q，两者均输入与门可得驱动信号Q2，两者均经过非门取反后输入与门可得驱动信号Q1。

4 半桥IB-APF仿真和实验验证

为验证所提APF及其控制方法的可行性，分别建立了仿真和实验模型，对其补偿效果和系统特性分别进行了仿真与实验，参数如表2所示。

表2 2kV·A（6kV·A）APF 系统参数Tab.2 Parameters of 2kV·A（6kV·A）prototype

试验中负载为8Ω电阻接10mH电感，电网输出有功功率约为5kW。

图 5所示为半桥IB-APF仿真关键波形，从上到下依次是电网电压uS、负载电流iL、电网电流iS以及补偿电流iC。补偿后的电网电流正弦且与电网电压相位一致，半桥并联型 IB-APF获得了良好的补偿效果。

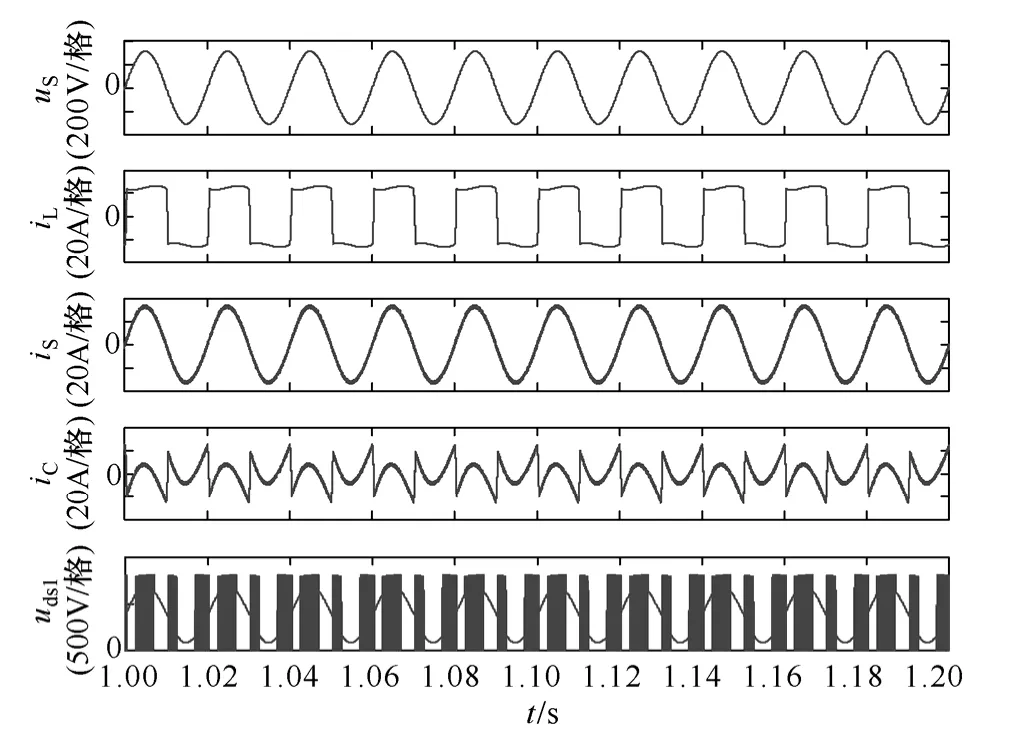
图5 半桥IB-APF 仿真关键波形Fig.5 Key simulation waveforms of half bridge IB-APF

桥臂中点输出电压和电感电流仿真波形如图 6所示，其中一组桥臂的中点输出电压呈现高频变化，而另一组则跟随电网电压变化，反之亦然，这与之前理论分析相同。电感电流为断续的直流高频变化量，设计时考虑其特点可以适当降低电感值，有助于成本和体积的减小。

图6 桥臂电压uEN、uFN和电感电流iL1、iL2仿真波形Fig.6 Simulation waveforms of uEN、uFNandiL1、iL2

图7 单相半桥IB-APF实验关键波形Fig.7 Key experimental waveforms in single-phase application

如图7所示半桥并联型IB-APF的实验关键波形，至上而下依次是电网电压uS、负载电流iL、电网电流iS、补偿电流iC以及直流侧电容电压Udc1、Udc2。此时直流侧电容电压均衡为400V。

对补偿前后的电网电压和电网电流进行 THD和FFT频谱分析，如图8所示。电网电压和电网电流THD值在补偿前分别为7.28%和28.42%，补偿后畸变率均得到了改善，分别降为4.64%和3.55%，半桥IB-APF取得了较好的补偿效果。电网电流中主要含量的3、5、7、9次谐波由24.64%、11.74%、5.99%和2.92%分别降为1.76%、0.61%、0.26%和1.72%。

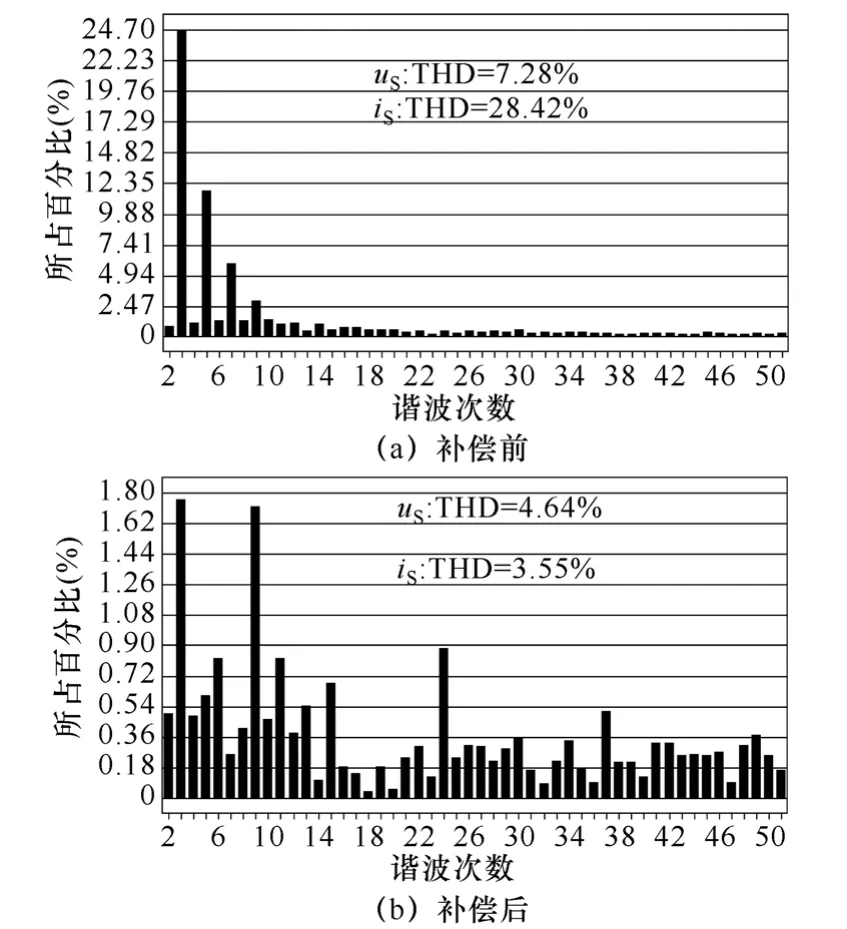
图8 单相系统补偿前后电网电流频谱分析Fig.8 Spectrum analysis of grid current before and after compensation

在相同的参数下建立三相半桥 IB-APF实验系统，负载为15Ω电阻串接20mH电感，得到如图9所示的A相实验关键波形，至上而下依次是电网电压、负载电流、电网电流以及补偿电流。此时，三相工频电网输出有功功率为16kV·A，电网电流峰值约为35A。

图9 三相半桥IB-APF实验A相关键波形Fig.9 Key experimental waveforms of phase-A in three-phase application

对补偿前后 A相电网电压和电网电流进行THD和FFT频谱分析，如图10所示。A相电网电压和电网电流的 THD由补偿前的 5.13%和 25.94%降为补偿后的3.18%和4.32%，大部分6n±1次谐波均受到抑制。

图10 三相系统补偿前后A相电网电流THD分析Fig.10 Spectrum analysis of phase-A grid current before and after compensation

通过上述仿真和实验结果可知，半桥并联型IB-APF在单相和三相系统中均取得了较好的补偿效果，验证了之前理论的正确性。

5 基于新型开关单元的一族IB-APF

5.1 新型三端口网络

IB电路的基本思想来源于传统半桥电路，因此IB-APF具有这两种电路的一般特点：直流侧需要两个分裂电容；需要两个功率开关管；直流电压利用率低。但 IB-APF独特的电路结构使其相对传统半桥型APF有其独特优势：避免桥臂直通，控制无需死区，有利于提高开关频率，APF损耗较低。

传统半桥APF为了获得更好的谐波补偿效果，需要将开关频率尽可能提高，因此导致死区时间在开关周期内比例加大，引起跟踪补偿误差，但是不加入死区又可能引起APF的安全运行，降低系统可靠性。同时，由于开关器件的体二极管性能较差，反向恢复电流大，恢复时间长，补偿电流经过体二极管续流会带来较大的损耗。相反，半桥 IB-APF的单管桥臂结构理想条件下完全杜绝了桥臂直通问题，免去了常规控制需要的死区时间[9,10]，不仅降低了控制的复杂性，更重要的是其减小了跟踪误差，提高了补偿精度，同时允许的情况下可以进一步提高开关频率。开关管和续流二极管的设计得到解耦，通过优选功率二极管，降低了APF的开关损耗。

传统的 DC-DC、DC-AC、AC-DC变换装置最基本的组成单元为如图11a、图11b、图11c所示的三种三端口网络（以下简称三端口网络a、b、c）。三端口网络 a和 b均由一个二极管 VD，一个双向开关管S和电感L组成，由于二极管的单向导电性，三个端口中始终存在两个端口之间仅能单相传输功率，如图中箭头方向所指，因此三端口网络a和b最常用于构建如Buck、Boost、Buck-Boost等DC-DC变换器，在交流系统中并无建树。为了满足三端口间功率能够双向流动，由双向开关管替代前两种三端口网络中的二极管，得到如图11c所示三端口网络c，由两个双向开关管S1、S2以及电感L构成，最常用于构建可控桥式 AC-DC、DC-AC变换器。值得注意的是，为了防止直流侧“+”“-”极短接，三端口网络a、b、c中y端口往往不会接入直流侧“+”极，而三端口网络c用于AC-DC、DC-AC变换器时，必须杜绝S1、S2同时导通的可能。

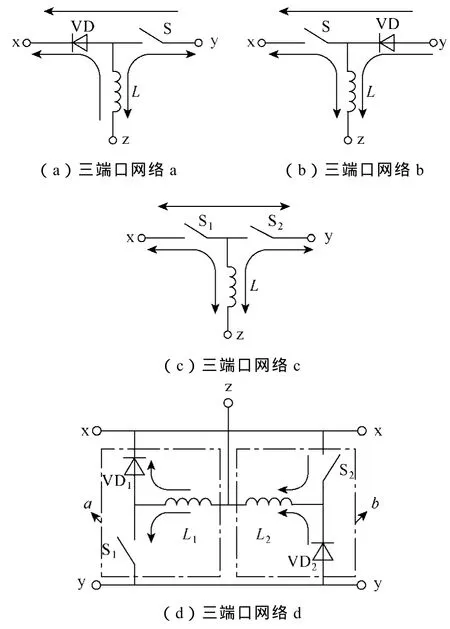
图11 几种三端口网络Fig.11 Several three-port netwoks

通过以上分析可知，为了构建交流功率变换装置，三端口网络中需要x与z、y与z两两端口间功率能够双向传输，而x与y之间功率的双向传输对功率变换而言有害无益。传统的双管桥臂结构通过增加死区来避免该双向通路，其隐患并没消除。

考虑到三端口网络 a、b中端口 x与 z、y与 z之间的功率传输通道正好互补，而x与y之间始终为单相传输通道，因此可以利用二者的并联结构构建新的三端口网络：三端口网络a、b中同名三端口均相连，可得如图 11d所示的三端口网络 d，三端口网络a、b成为d的子网络。d中x与z之间功率的双向传输分别通过三端子网络a、b来实现，y与z之间功率的双向传输亦是如此，如图中箭头所指。因此，三端口网络 d可以替代三端口网络 c，构成新型的交流功率变流器，并带来更佳的性能。这里命名该网络为交错降压式开关单元。

5.2 一族并联型IB-APF

基于三端口网络d提出一族新颖的APF拓扑，如图12a～图12f所示。

图12 一族新型APF的6种拓扑Fig.12 The six basic topologies of the new APF

图 12a所示为半桥 IB-APF拓扑，这里不再赘述。

将传统全桥 APF中双管三端口网络结构替换为交错降压式三端口网络结构，得到如图12b所示的全桥 IB-APF拓扑。该拓扑克服了半桥结构的直流侧电压利用率较低的问题，降低了系统成本和损耗，无需均压，简化了控制系统，更有利于提高APF的实用性和补偿效果。

为了保证有源电力滤波器具备良好的补偿特性，有必要尽可能提高开关频率。但是在高功率环境中，开关器件首先面对的就是功率高低和工作频率大小间的直接矛盾。为了缓解开关器件在功率等级和开关频率间的矛盾，提高电力电子装置对大功率的处理能力，人们对电力电子装置及其控制手段进行了大量的探索研究，其最具代表性的科研成果是多重化技术、相移SPWM组合变流器以及多电平变流器等。其基本思想均是采用多个相同或相似模块（开关器件）构建成新的电力电子装置，对应一定的控制手段，减轻单开关器件的功率压力。文献[15]首先将H桥级联型变流器应用至电能质量治理领域，并受到广泛关注，当然，也有采用半桥拓扑进行级联的变换器。将传统级联APF中双管三端口网络结构替换为交错降压式三端口网络结构，则可以得到半桥级联IB-APF拓扑（图12c）和全桥级联IB-APF拓扑（图12d）。将全桥级联IB-APF拓扑中的部分交错降压式三端口网络还原为双管三端口网络，按照不同的链接方式又可以得到如图12e和图12f所示的混合型全桥级联IB-APF拓扑，注意其中的功率管S5～S8工作在电网频率，因此可以直接串联从而可以使得电路更加简洁，这两种拓扑形式具有相同特性，且由于两种三端口网络的混合运用有效减少了APF的接口电感。

6 结论

本文提出了一族基于交错降压开关单元的新型有源电力滤波器拓扑，并以基于该开关单元的半桥有源电力滤波器为例进行了详细的原理分析和实验验证。仿真和实验结果表明该开关单元解决了桥臂直通隐患，并且可以实现无死区控制，功率管和二极管的设计可实现解耦和分别优化。相对于传统拓扑，文中所提拓扑中所需要的电感数目有所增加，未来可通过磁性元件耦合的方法进一步简化；而调制方式并未增加过多的复杂度。因此，总体而言该有源滤波器族具有独特的特性和优势，适用于高可靠性、高效、高性能的应用场合。

[1] 王兆安, 杨君, 刘进军. 谐波抑制与无功功率补偿[M]. 北京: 机械工业出版社, 1998.

[2] Akagi H, Watanabe E, Aredes M. Instantaneous power theory and applications to power conditioning[M]. Piscataway, NJ: IEEE Press, 2007.

[3] 吴传平, 罗安, 帅智康, 等. 注入式混合有源电力滤波器的数学模型及其特性[J]. 中国电机工程学报,2009, 29(36): 35-41.

Wu Chuanping, Luo An, Shuai Zhikang, et al.Mathematical model and characteristics of injection type hybrid active power filter[J]. Proceedings of the CSEE, 2009, 29(36): 35-41.

[4] 李红雨, 吴隆辉, 卓放, 等. 一种新型的快速电流检测方法的研究[J]. 中国电机工程学报, 2005,25(13): 57-62.

Li Hongyu, Wu Longhui, Zhuo Fang, et al. Study on the novel fast current detection method[J]. Proceedings of the CSEE, 2005, 25(13): 57-62.

[5] 刘宏超, 彭建春. 三相四开关并联型有源电力滤波器的指令电流确定方法[J]. 中国电机工程学报,2009, 29(16): 108-113.

Liu Hongchao, Peng Jianchun. Study on current command signal of three-phase four-switch shunt active power filter[J]. Proceedings of the CSEE, 2009,29(16): 108-113.

[6] 侯世英, 郑含博, 周雒维, 等. 双环控制整流桥直流侧串联型有源电力滤波器及实验研究[J]. 中国电机工程学报, 2009, 29(4): 78-83.

Hou Shiying, Zheng Hanbo, Zhou Luowei, et al.DC-side series active power filter and experimental study with dual control[J]. Proceedings of the CSEE,2009, 29(4): 78-83.

[7] 郭伟峰, 徐殿国, 武健, 等. LCL有源电力滤波器新型控制方法[J]. 中国电机工程学报, 2010, 30(3):42-48.

Guo Weifeng, Xu Dianguo, Wu Jian, et al. Novel control method for LCL active power fitler[J].Proceedings of the CSEE, 2010, 30(3): 42-48.

[8] 陈仲, 罗颖鹏, 石磊, 等. 并联型 APF两种典型控制方式的机制解析[J]. 中国电机工程学报, 2010,30(33): 37-43.

Chen Zhong, Luo Yingpeng, Shi Lei, et al. Analysis on mechanisms on two typical control schemes for parallel APF[J]. Proceedings of the CSEE, 2010,30(33): 37-42.

[9] Oliveira A C, Jacobina C B, Lima A M N. Improved dead-time compensation for sinusoidal PWM inverters operating at high switching frequencies[J]. IEEE Transactions on Industrial Electronics, 2007, 54(4):2295-2304.

[10] Attaianese C, Tomasso G. Predictive compensation of dead-time effects in VSI feeding induction motors[J].IEEE Transactions on Industry Applications, 2001,37(3): 856-863.

[11] Zargan N R, Ziogas P D, Geza J. A two-switch highperformance current regulated DC/AC converter module[J]. IEEE Transactions on Industry Applications, 1995,31(3): 583-589.

[12] Stanley G R, Bradshaw K M. Precision DC-to-AC power conversion by optimization of the output current waveform-the half bridge revisited[J]. IEEE Transactions on Power Electronic, 1999, 14(2): 372-380.

[13] Stanley G R. Opposed current power converter: U. S.,5657219[P]. 1997.

[14] Stanley G R. Half-bridge gate driver optimized for hard-switching: U. S., 6556053 B2[P]. 2003.

[15] Peng F Z, Lai J S, John W M, et al. A multilevel voltage source inverter with separate DC source for static var generation[J]. IEEE Transactions on Industry Applications, 1996, 32(5): 1130-1137.